7.3.2《多边形的内角和》精品课件(人教版七年级)
文档属性
| 名称 | 7.3.2《多边形的内角和》精品课件(人教版七年级) |
|
|
| 格式 | zip | ||
| 文件大小 | 505.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-27 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
据历史记载,诸葛村整体结构是诸葛亮第27代裔诸葛大狮按九宫八卦设计布局的,整个村落以钟池为核心,八条小巷向外辐射,形成内八卦,更为神奇的村外八座小山环抱整个村落,构成外八卦.
诸葛八卦村,位于浙江中西部兰溪市境内,距市区18公里,村中现居有诸葛亮后裔近4000人,为全国诸葛亮后裔最大聚居地.
1. 从n边形的一个顶点可以引_____条对角线,
将n边形分成了________个三角形.
2. n边形的对角线一共有______ 条.
(n-3)
(n-2)
温故知新
问题2:你知道长方形和正方形的内角和是多少吗?
其他四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度吗?
(三角形内角和 180°)
(都是360°)
想一想
四边形内角和为360°
B
A
C
D
E
探究1
五边形内角和=3×180°=540°
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 计算规律
三边形
四边形
五边形
六边形
n边形
…
…
…
…
…
…
3
4
5
6
n
0
n-3
1
2
3
1
2
3
4
n-2
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180° × 4 – 180° = 540°
E
A
B
C
D
O
180°× 5 – 360°= 540°
A
B
C
D
E
4 × 180°-180 °
O
=540°
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
【例1】已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?
A
B
C
D
点评:如果四边形的一组对角互补,那么另一组对角也互补.
解:四边形的内角和为
(4 - 2) ×180 =360 °,
所以 ∠B+∠D= 360 °- (A+∠C)=180°.
∠A+∠C=180°,
十二边形的内角和是( ).
一个多边形当边数增加1时,它的内角和增加( ).
一个多边形的内角和是720 ,则此多边形共有( )个内角.
如果一个多边形的内角和是1440°,那么这是( )边形.
1800
180
六
十
【例2】如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
五边形外角和
结论:五边形的外角和等于360°.
-(5-2) × 180°
=360 °
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-五边形内角和
=5×180°
【例2】如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
探究 在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
结论:n边形的外角和等于360°.
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
=n个平角-n边形内角和
= n×180 °
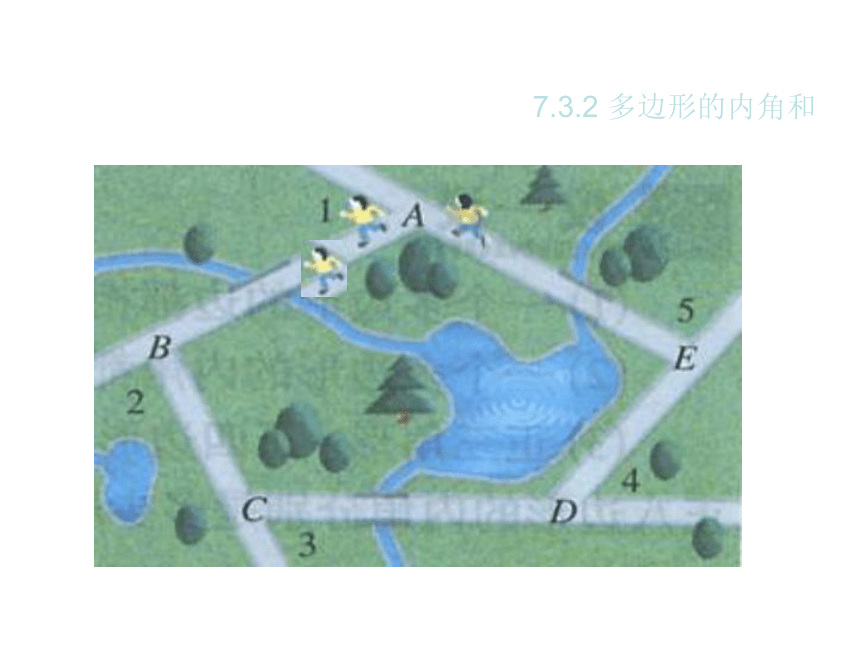
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向.在行程中所转的各个角的和是多少?
多边形的外角和
每个内角的度数是
每个外角的度数是
练习1:兰溪八卦村构成的八卦图形实质是正八边形,它的每一个内角相等,那么正八边形的每一个外角等于____,每一个内角等于_____.
8x=360°
x=45°
135°
45°
解:设正八边形的每一个外角度数为x,由
“多边形的外角和等于360度”可得:
所以每一个内角度数为135°.
练习2: 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360 ,
∴ (n-2) 180°=2× 360 .
解得: n=6.
∴这个多边形的边数为6.
填空题
(1)一个多边形的内角和为4320°,则它的边数为______
(2)五边形的内角和为_____,它的对角线共有_____条
(3)一个多边形的每一个外角都等于30°,则这个多边形为____边形
(4)一个多边形的每一个内角都等于135°,则这个多边形为_____边形
(5)如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
(1)n边形的n个内角中锐角最多有______个
(2)把一个四边形削去一个角,剩下一个几边形?它的内角和是多少?
据历史记载,诸葛村整体结构是诸葛亮第27代裔诸葛大狮按九宫八卦设计布局的,整个村落以钟池为核心,八条小巷向外辐射,形成内八卦,更为神奇的村外八座小山环抱整个村落,构成外八卦.
诸葛八卦村,位于浙江中西部兰溪市境内,距市区18公里,村中现居有诸葛亮后裔近4000人,为全国诸葛亮后裔最大聚居地.
1. 从n边形的一个顶点可以引_____条对角线,
将n边形分成了________个三角形.
2. n边形的对角线一共有______ 条.
(n-3)
(n-2)
温故知新
问题2:你知道长方形和正方形的内角和是多少吗?
其他四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度吗?
(三角形内角和 180°)
(都是360°)
想一想
四边形内角和为360°
B
A
C
D
E
探究1
五边形内角和=3×180°=540°
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 计算规律
三边形
四边形
五边形
六边形
n边形
…
…
…
…
…
…
3
4
5
6
n
0
n-3
1
2
3
1
2
3
4
n-2
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180° × 4 – 180° = 540°
E
A
B
C
D
O
180°× 5 – 360°= 540°
A
B
C
D
E
4 × 180°-180 °
O
=540°
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
【例1】已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?
A
B
C
D
点评:如果四边形的一组对角互补,那么另一组对角也互补.
解:四边形的内角和为
(4 - 2) ×180 =360 °,
所以 ∠B+∠D= 360 °- (A+∠C)=180°.
∠A+∠C=180°,
十二边形的内角和是( ).
一个多边形当边数增加1时,它的内角和增加( ).
一个多边形的内角和是720 ,则此多边形共有( )个内角.
如果一个多边形的内角和是1440°,那么这是( )边形.
1800
180
六
十
【例2】如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
6
E
B
C
D
1
2
3
4
5
A
五边形外角和
结论:五边形的外角和等于360°.
-(5-2) × 180°
=360 °
6
E
B
C
D
1
2
3
4
5
A
=5个平角
-五边形内角和
=5×180°
【例2】如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
探究 在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
结论:n边形的外角和等于360°.
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
=n个平角-n边形内角和
= n×180 °
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向.在行程中所转的各个角的和是多少?
多边形的外角和
每个内角的度数是
每个外角的度数是
练习1:兰溪八卦村构成的八卦图形实质是正八边形,它的每一个内角相等,那么正八边形的每一个外角等于____,每一个内角等于_____.
8x=360°
x=45°
135°
45°
解:设正八边形的每一个外角度数为x,由
“多边形的外角和等于360度”可得:
所以每一个内角度数为135°.
练习2: 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360 ,
∴ (n-2) 180°=2× 360 .
解得: n=6.
∴这个多边形的边数为6.
填空题
(1)一个多边形的内角和为4320°,则它的边数为______
(2)五边形的内角和为_____,它的对角线共有_____条
(3)一个多边形的每一个外角都等于30°,则这个多边形为____边形
(4)一个多边形的每一个内角都等于135°,则这个多边形为_____边形
(5)如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
(1)n边形的n个内角中锐角最多有______个
(2)把一个四边形削去一个角,剩下一个几边形?它的内角和是多少?
