第十八章 平行四边形章末复习:微专题6 正方形中全等三角形的证明(含答案)
文档属性
| 名称 | 第十八章 平行四边形章末复习:微专题6 正方形中全等三角形的证明(含答案) | 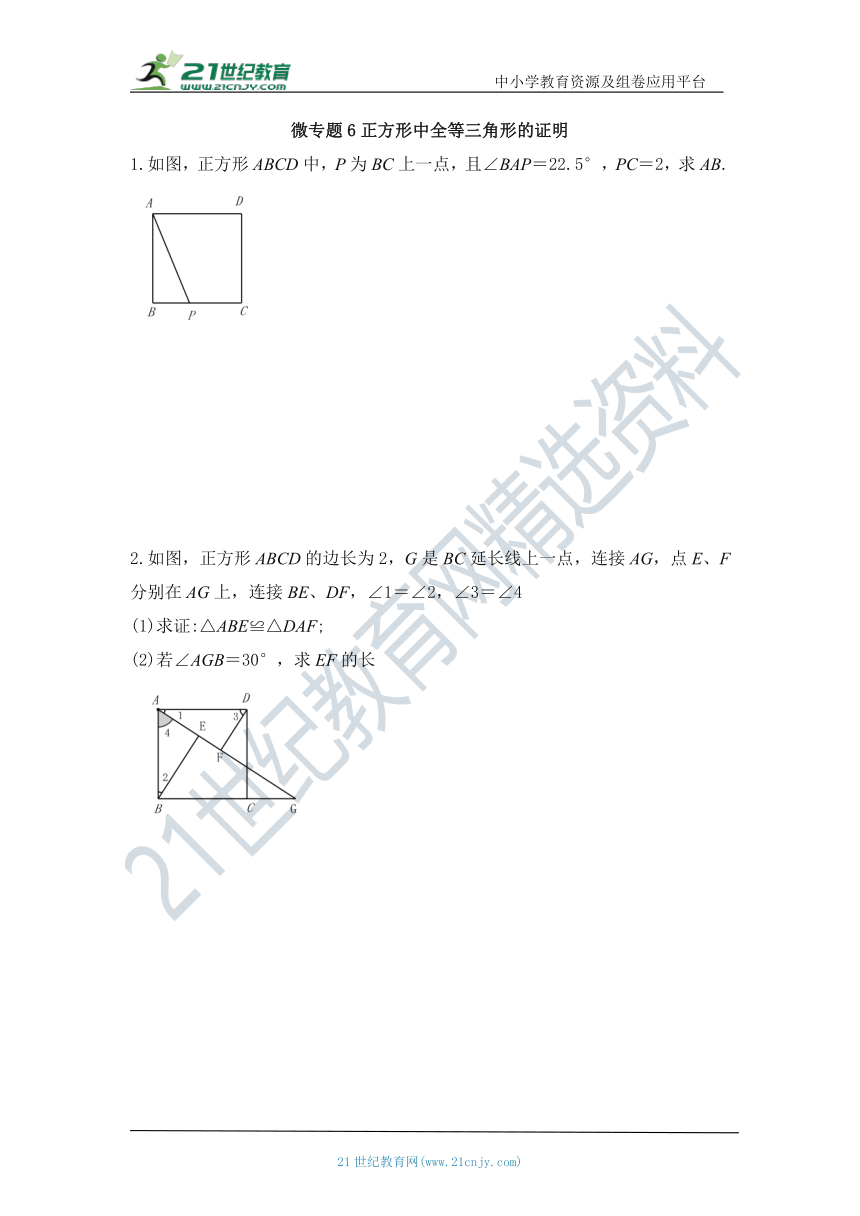 | |
| 格式 | docx | ||
| 文件大小 | 130.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 05:56:49 | ||
图片预览


文档简介
微专题6正方形中全等三角形的证明
1.如图,正方形ABCD中,P为BC上一点,且∠BAP=22.5°,PC=2,求AB.
2.如图,正方形ABCD的边长为2,G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4
(1)求证:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长
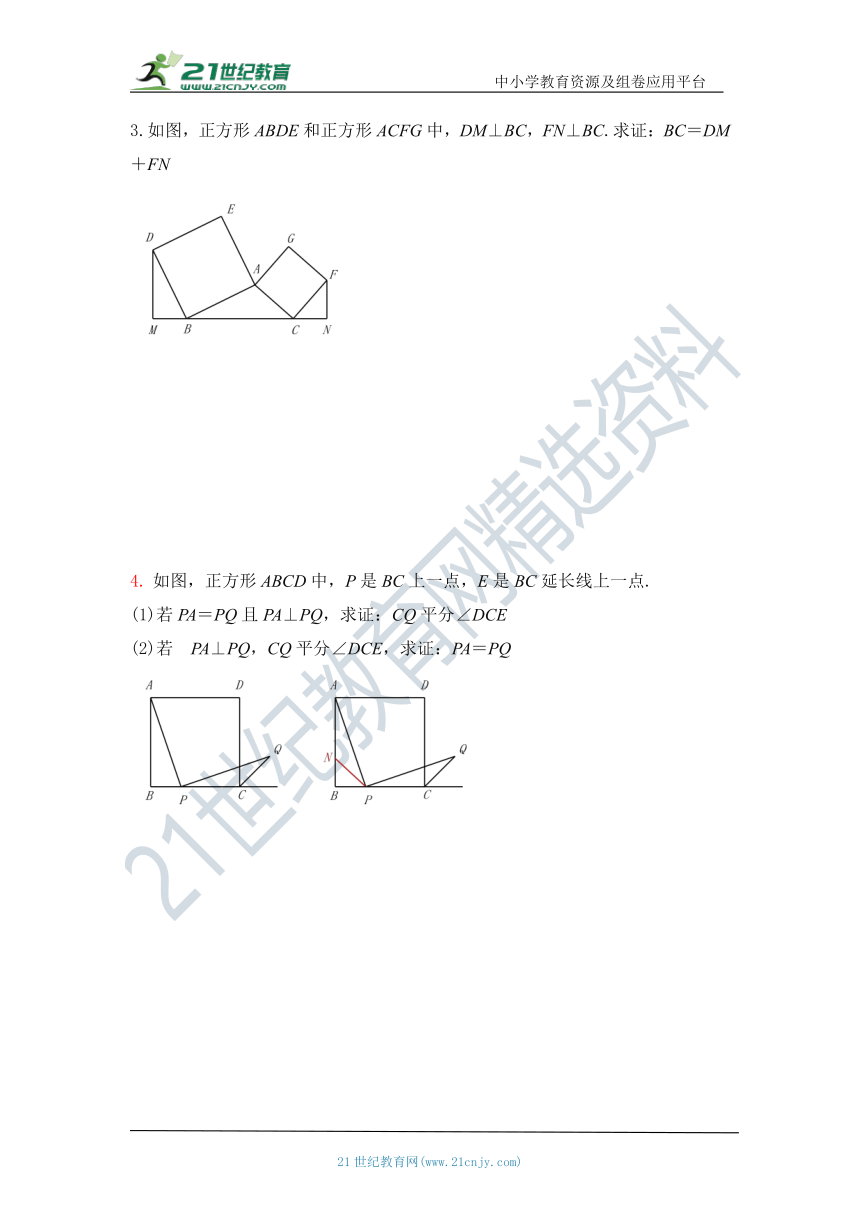
3.如图,正方形ABDE和正方形ACFG中,DM⊥BC,FN⊥BC.求证:BC=DM+FN
如图,正方形ABCD中,P是BC上一点,E是BC延长线上一点.
(1)若PA=PQ且PA⊥PQ,求证:CQ平分∠DCE
(2)若?PA⊥PQ,CQ平分∠DCE,求证:PA=PQ
5.如图,点E是正方形ABCD的边CD上一点(不与C、D重合),连接AE,过点A作AF⊥AE,交CB的延长线于点F.
(1)判断△AEF的形状并证明;
(2)连接EF,取EF的中点M,连接BM,当E在CD上移动时,BM与CE之间是否存在某种确定的数量关系?请写出结论并证明;
(3)在(2)的条件下求false的值;
(4)以BF为边作正方形BFHG,AF与CG相交于P点,当点E在边CD上运动时(不与C、D重合),问∠APD的大小是否发生变化?若不变,请求其值;若变化,请说明理由.
微专题6正方形中全等三角形的证明
1.如图,正方形ABCD中,P为BC上一点,且∠BAP=22.5°,PC=2,求AB.
解:连接AC,过P作PE⊥AC
∵四边形ABCD为正方形
∴∠BAP=∠EAP=22.5°∠B=∠AEP=90°
又∵AP=AP ∴△ABP≌△AEP(AAS)
∴∠EPC=180°-∠BPA-∠EPA=45°.
∴BP=EP,∠BPA=∠EPA=90°-∠BAP=67.5°
∴∠EPC=∠ECP
又∵PE⊥CE,PC=2 ∴PE=false,BP=false,∴AB=BC=2+false
2.如图,正方形ABCD的边长为2,G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4
(1)求证:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长
(1)证明:∵∠1=∠2,∠3=∠4,AB=AD
∴△ABE≌△DAF(ASA)
(2)解:∵四边形ABCD为正方形
∴AD∥BC,∠ABG=90°
∴∠1=∠AGB=30°,∠4=90°-∠AGB=60°
∴∠2+∠4=∠1+∠3=90°
∴BE⊥AG,DF⊥AG
∵AE=1,AF=false,则EF=AF-AE=false-1
3.如图,正方形ABDE和正方形ACFG中,DM⊥BC,FN⊥BC.求证:BC=DM+FN
证明:过点A作AP⊥BC
∵四边形ABDE为正方形
∴DB⊥AB且DB=AB ∴∠DBM+∠PBA=90°
又∵DM⊥BC
∴∠MDB+∠DBM=90°∵∠MDB=∠PBA
又∵AP⊥BC
∴∠M=∠APB
又∵DB=AB
∴△MDB≌△PBA(AAS) ∴DM=BP
同理可得FN=PC
∴BC=BP+PC=DM+FN
4.如图,正方形ABCD中,P是BC上一点,E是BC延长线上一点.
(1)若PA=PQ且PA⊥PQ,求证:CQ平分∠DCE
(2)若?PA⊥PQ,CQ平分∠DCE,求证:PA=PQ
证明:在线段AB上取点N,使得AN=PC,连PN
(1)∵PA⊥PQ ∴∠APB+∠QPC=90°
又∵四边形ABCD为正方形 ∴∠B=90°AB=BC,∴∠PAN+∠APB=90°∴∠PAN=∠QPC
又∵AN=PC,PA=PQ ∴△PAN≌△QPC(SAS) ∴∠ANP=∠PCQ
∵AB=BC,AN=PC,∴BN=BP
∴∠BNP=45°∴∠ANP=135°=∠PCQ ∴∠QCE=45° ∴CQ平分∠DCE
(2) ∵CQ平分∠DCE ∴∠QCE=45°
又∵四边形ABCD为正方形 ∴∠PCD=90 ∵∠PCQ=135°
由(1)知∠ANP=135°=∠PCQ ∠PAN=∠QPC
又∵AN=PC ∴△PAN△QPC(ASA) ∴PA=PO
5.如图,点E是正方形ABCD的边CD上一点(不与C、D重合),连接AE,过点A作AF⊥AE,交CB的延长线于点F.
(1)判断△AEF的形状并证明;
(2)连接EF,取EF的中点M,连接BM,当E在CD上移动时,BM与CE之间是否存在某种确定的数量关系?请写出结论并证明;
(3)在(2)的条件下求false的值;
(4)以BF为边作正方形BFHG,AF与CG相交于P点,当点E在边CD上运动时(不与C、D重合),问∠APD的大小是否发生变化?若不变,请求其值;若变化,请说明理由.
解:(1)△AEF为等腰直角三角形
证明:∵四边形ABCD为正方形
∴∠D=∠BAD=∠ABC=90°,AB=AD ∴∠BAE+∠DAE=90°
∴∠ABF=90
又∵AF⊥AE ∴∠BAF+∠BAE=90°∴∠BAF=∠DAE
又∵AB=AD,∠ABF=∠ADE=90°
∴△ABP≌△ADE(AAS),∴AF=AE ∴△AEF为等腰直角三角形
(2)CE=falseBM
证明:在BC上截取CN=EC,连接EN,∴DE=BN,由(1)知BF=DE=BN ∴BM为△FNE中位线
∴BM=falseNE,而NE=falseCE,∴CE=falseBM
(3) false=false=false=false=false
(4)可证△CGB≌△AFB ∴可得CP⊥AF,且CG=AF 过D作DR⊥PD交PC的延长线于R.
∵∠APC=∠PDR=90° ∴∠APD=∠CRD ∵∠ADC=∠PDR ∴∠ADP=∠CDR 又∵AD=CD,∴△DAP≌△DCR(AAS), ∴PD=DR ∴∠DPF=45°∴∠APD=45°
1.如图,正方形ABCD中,P为BC上一点,且∠BAP=22.5°,PC=2,求AB.
2.如图,正方形ABCD的边长为2,G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4
(1)求证:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长
3.如图,正方形ABDE和正方形ACFG中,DM⊥BC,FN⊥BC.求证:BC=DM+FN
如图,正方形ABCD中,P是BC上一点,E是BC延长线上一点.
(1)若PA=PQ且PA⊥PQ,求证:CQ平分∠DCE
(2)若?PA⊥PQ,CQ平分∠DCE,求证:PA=PQ
5.如图,点E是正方形ABCD的边CD上一点(不与C、D重合),连接AE,过点A作AF⊥AE,交CB的延长线于点F.
(1)判断△AEF的形状并证明;
(2)连接EF,取EF的中点M,连接BM,当E在CD上移动时,BM与CE之间是否存在某种确定的数量关系?请写出结论并证明;
(3)在(2)的条件下求false的值;
(4)以BF为边作正方形BFHG,AF与CG相交于P点,当点E在边CD上运动时(不与C、D重合),问∠APD的大小是否发生变化?若不变,请求其值;若变化,请说明理由.
微专题6正方形中全等三角形的证明
1.如图,正方形ABCD中,P为BC上一点,且∠BAP=22.5°,PC=2,求AB.
解:连接AC,过P作PE⊥AC
∵四边形ABCD为正方形
∴∠BAP=∠EAP=22.5°∠B=∠AEP=90°
又∵AP=AP ∴△ABP≌△AEP(AAS)
∴∠EPC=180°-∠BPA-∠EPA=45°.
∴BP=EP,∠BPA=∠EPA=90°-∠BAP=67.5°
∴∠EPC=∠ECP
又∵PE⊥CE,PC=2 ∴PE=false,BP=false,∴AB=BC=2+false
2.如图,正方形ABCD的边长为2,G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4
(1)求证:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长
(1)证明:∵∠1=∠2,∠3=∠4,AB=AD
∴△ABE≌△DAF(ASA)
(2)解:∵四边形ABCD为正方形
∴AD∥BC,∠ABG=90°
∴∠1=∠AGB=30°,∠4=90°-∠AGB=60°
∴∠2+∠4=∠1+∠3=90°
∴BE⊥AG,DF⊥AG
∵AE=1,AF=false,则EF=AF-AE=false-1
3.如图,正方形ABDE和正方形ACFG中,DM⊥BC,FN⊥BC.求证:BC=DM+FN
证明:过点A作AP⊥BC
∵四边形ABDE为正方形
∴DB⊥AB且DB=AB ∴∠DBM+∠PBA=90°
又∵DM⊥BC
∴∠MDB+∠DBM=90°∵∠MDB=∠PBA
又∵AP⊥BC
∴∠M=∠APB
又∵DB=AB
∴△MDB≌△PBA(AAS) ∴DM=BP
同理可得FN=PC
∴BC=BP+PC=DM+FN
4.如图,正方形ABCD中,P是BC上一点,E是BC延长线上一点.
(1)若PA=PQ且PA⊥PQ,求证:CQ平分∠DCE
(2)若?PA⊥PQ,CQ平分∠DCE,求证:PA=PQ
证明:在线段AB上取点N,使得AN=PC,连PN
(1)∵PA⊥PQ ∴∠APB+∠QPC=90°
又∵四边形ABCD为正方形 ∴∠B=90°AB=BC,∴∠PAN+∠APB=90°∴∠PAN=∠QPC
又∵AN=PC,PA=PQ ∴△PAN≌△QPC(SAS) ∴∠ANP=∠PCQ
∵AB=BC,AN=PC,∴BN=BP
∴∠BNP=45°∴∠ANP=135°=∠PCQ ∴∠QCE=45° ∴CQ平分∠DCE
(2) ∵CQ平分∠DCE ∴∠QCE=45°
又∵四边形ABCD为正方形 ∴∠PCD=90 ∵∠PCQ=135°
由(1)知∠ANP=135°=∠PCQ ∠PAN=∠QPC
又∵AN=PC ∴△PAN△QPC(ASA) ∴PA=PO
5.如图,点E是正方形ABCD的边CD上一点(不与C、D重合),连接AE,过点A作AF⊥AE,交CB的延长线于点F.
(1)判断△AEF的形状并证明;
(2)连接EF,取EF的中点M,连接BM,当E在CD上移动时,BM与CE之间是否存在某种确定的数量关系?请写出结论并证明;
(3)在(2)的条件下求false的值;
(4)以BF为边作正方形BFHG,AF与CG相交于P点,当点E在边CD上运动时(不与C、D重合),问∠APD的大小是否发生变化?若不变,请求其值;若变化,请说明理由.
解:(1)△AEF为等腰直角三角形
证明:∵四边形ABCD为正方形
∴∠D=∠BAD=∠ABC=90°,AB=AD ∴∠BAE+∠DAE=90°
∴∠ABF=90
又∵AF⊥AE ∴∠BAF+∠BAE=90°∴∠BAF=∠DAE
又∵AB=AD,∠ABF=∠ADE=90°
∴△ABP≌△ADE(AAS),∴AF=AE ∴△AEF为等腰直角三角形
(2)CE=falseBM
证明:在BC上截取CN=EC,连接EN,∴DE=BN,由(1)知BF=DE=BN ∴BM为△FNE中位线
∴BM=falseNE,而NE=falseCE,∴CE=falseBM
(3) false=false=false=false=false
(4)可证△CGB≌△AFB ∴可得CP⊥AF,且CG=AF 过D作DR⊥PD交PC的延长线于R.
∵∠APC=∠PDR=90° ∴∠APD=∠CRD ∵∠ADC=∠PDR ∴∠ADP=∠CDR 又∵AD=CD,∴△DAP≌△DCR(AAS), ∴PD=DR ∴∠DPF=45°∴∠APD=45°
