第十八章 平行四边形章末复习:微专题7 正方形中45°角的问题(含答案)
文档属性
| 名称 | 第十八章 平行四边形章末复习:微专题7 正方形中45°角的问题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 152.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 00:00:00 | ||
图片预览



文档简介
微专题7 正方形中45°角的问题
1.如图,在四边形ABCD中,∠BAD=45°,∠BCD=90°,CA平分∠BCD,若AC=6false,BD=5,求四边形ABCD的面积.
2.如图,在四边形AECD中,∠E=∠C=90°,AE=CE,M为EC上一点,若∠MAD=45°,CD=6,
CM=8,求EM的长.
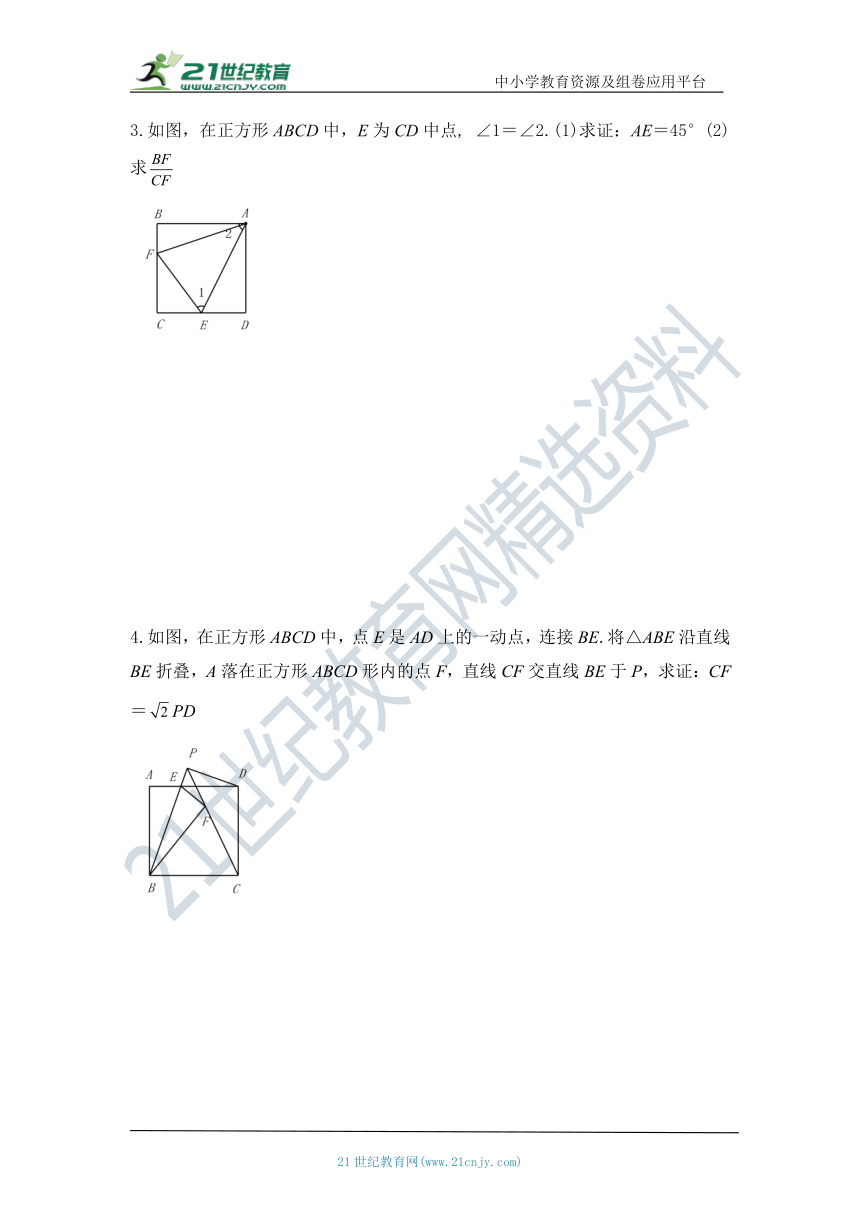
3.如图,在正方形ABCD中,E为CD中点, ∠1=∠2.(1)求证:AE=45°(2)求false
4.如图,在正方形ABCD中,点E是AD上的一动点,连接BE.将△ABE沿直线BE折叠,A落在正方形ABCD形内的点F,直线CF交直线BE于P,求证:CF=falsePD
5.如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF=false,点G、H别为AB、CD边上的点,连接GH,若线段GH与EF的夹角为45°,求GH的长.
6.已知,正方形ABCD中,点M、N为AB、CD上的点,AP⊥M于E,交BC于P.
(1)如图1,求证:AP=MN;
(2)如图2,若EA=EF,连CF,点G为CF中点,连DG、DE,求证:DE=falseDG;
(3)在(2)的条件下,若DA=DE,且DN=false,BM=2,则DG=false.
7.点P为正方形ABCD外一点
(1)如图1,∠APB=45°,∠ABP=30°,求证:AB=falseAP
(2)如图2,PB平分∠APC,AE⊥BP,连DP,求证:PB+PD=2BE;
(3)如图3,AB=1,PA//BD,PB=BD,则PA=false;∠APB=30°
微专题7 正方形中45°角的问题
1.如图,在四边形ABCD中,∠BAD=45°,∠BCD=90°,CA平分∠BCD,若AC=6false,BD=5,求四边形ABCD的面积.
解:过点A作AQ⊥CD,AP⊥BC,垂足分别为Q、P,则四边形AQCP为正方形
延长BP至G,使GP=DQ,易证△AGP≌△ADQ(SAS),则AG=AD,∠GAP=∠DAQ
由∠BAD=45°可得∠GAB=45°,则△GAB≌△BAD(SAS)∴BD=GB
s=S正方形APCQ-S△AGB=36-falseGB×AP=36-false×5×6=21
2.如图,在四边形AECD中,∠E=∠C=90°,AE=CE,M为EC上一点,若∠MAD=45°,CD=6,
CM=8,求EM的长.
解:延长CD,作AF⊥CD于点F,则四边形AECF为正方形
延长CF至B,使BF=ME,易证△AEM≌△AFB(SAS),则AM=AB,∠EAM=∠FAB
由∠BAD=45°,则∠EAM+∠DAF=45°
∴∠DAB=45°,则△MAD≌△BAD(SAS) ∴BD=MD=10
设EM=x ∴DF=10-x=8+x-6; x=4,即EM=4
3.如图,在正方形ABCD中,E为CD中点, ∠1=∠2.(1)求证:AE=45°(2)求false
(1)证明:过A作AM⊥EF ∵AB∥CD ∴∠AED=∠1
∵∠1=∠2 ∴∠AED=∠2 又∵AE=AE ∠D=∠AME=90°
∴△AEM≌△AED(AAS) ∴AM=AD ∠MAE=∠DAE
同理可证△ABF≌△AMF ∴∠BAF=∠FAM ∴∠FAE=false∠BAD=45°
(2)解:设正方形边长为2a BF=x ∵E为CD中点,∴DE=CE=a,CF=2a-x
由(1)知FE=BF+DE=a+x 在Rt△CEP中,由勾股定理得a2+(2a-x)2=(a+x)2
∴x=false∴false=false
4.如图,在正方形ABCD中,点E是AD上的一动点,连接BE.将△ABE沿直线BE折叠,A落在正方形ABCD形内的点F,直线CF交直线BE于P,求证:CF=falsePD
证明:作DQ⊥PC,BH⊥FC,易证△DQC≌△CHB ∴DQ=HC=HF
易证BH=HP=QC ∴PQ=HC=HF ∴PD=falsePQ=falseHC
而FC=2HC,∴?FC=falsePD
5.如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF=false,点G、H别为AB、CD边上的点,连接GH,若线段GH与EF的夹角为45°,求GH的长.
解:过B作BM//EF,BN//GH由题意得∠MBN=45
∴AM+CN=MN
又∵EF=false,AB=2,∴AM=1,设NC=x
∴DN=2-x,MN=x+1∴(x+1)2=(2-x)2+1,∴x=false
∴GH=BN=false
6.已知,正方形ABCD中,点M、N为AB、CD上的点,AP⊥M于E,交BC于P.
(1)如图1,求证:AP=MN;
(2)如图2,若EA=EF,连CF,点G为CF中点,连DG、DE,求证:DE=falseDG;
(3)在(2)的条件下,若DA=DE,且DN=false,BM=2,则DG=false.
证明:(1)作BF//MN,∴四边形MBFN为平行四边形∴MN=BF
可证△BFC≌△APB,∴BF=AP,∴AP=MN
(2)连EG并延长使得EG=QG,连CQ,∴CQ平行且等于EF
连DQ,可证∠DCQ=∠CNE=∠EAD且CQ=EF=AE
∴易证△DAE≌△DCQ,∴DE⊥DQ且DE=DQ
∴△DEG为等腰Rt△,∴DE=falseDG
7.点P为正方形ABCD外一点
(1)如图1,∠APB=45°,∠ABP=30°,求证:AB=falseAP
(2)如图2,PB平分∠APC,AE⊥BP,连DP,求证:PB+PD=2BE;
(3)如图3,AB=1,PA//BD,PB=BD,则PA=false;∠APB=30°
证明:(1)作AM⊥BP,设AM=a
AP=falsea,而AB=2a,∴AB=falseAP
(2)作BM⊥PC,BN⊥AP
∴BP平分∠APC,∴BN=BM,又∵BA=BC,∴△ABN≌△CBM,∴∠MAB=∠MCB
∴∠BAP+∠BCP=180°,∴∠ABC+∠APC=180°,∴∠APB=∠BPC=45°
作CQ⊥PC交PB的延长线于点Q,可证△PDC≌△QBC
∴∠Q=∠DPC=45°,∴PD+PB=falsePC
过C作CH⊥BP,可证CH=BE
又∵PC=falseHC,∴PC=falseBE,∴PB+PD=2BE
1.如图,在四边形ABCD中,∠BAD=45°,∠BCD=90°,CA平分∠BCD,若AC=6false,BD=5,求四边形ABCD的面积.
2.如图,在四边形AECD中,∠E=∠C=90°,AE=CE,M为EC上一点,若∠MAD=45°,CD=6,
CM=8,求EM的长.
3.如图,在正方形ABCD中,E为CD中点, ∠1=∠2.(1)求证:AE=45°(2)求false
4.如图,在正方形ABCD中,点E是AD上的一动点,连接BE.将△ABE沿直线BE折叠,A落在正方形ABCD形内的点F,直线CF交直线BE于P,求证:CF=falsePD
5.如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF=false,点G、H别为AB、CD边上的点,连接GH,若线段GH与EF的夹角为45°,求GH的长.
6.已知,正方形ABCD中,点M、N为AB、CD上的点,AP⊥M于E,交BC于P.
(1)如图1,求证:AP=MN;
(2)如图2,若EA=EF,连CF,点G为CF中点,连DG、DE,求证:DE=falseDG;
(3)在(2)的条件下,若DA=DE,且DN=false,BM=2,则DG=false.
7.点P为正方形ABCD外一点
(1)如图1,∠APB=45°,∠ABP=30°,求证:AB=falseAP
(2)如图2,PB平分∠APC,AE⊥BP,连DP,求证:PB+PD=2BE;
(3)如图3,AB=1,PA//BD,PB=BD,则PA=false;∠APB=30°
微专题7 正方形中45°角的问题
1.如图,在四边形ABCD中,∠BAD=45°,∠BCD=90°,CA平分∠BCD,若AC=6false,BD=5,求四边形ABCD的面积.
解:过点A作AQ⊥CD,AP⊥BC,垂足分别为Q、P,则四边形AQCP为正方形
延长BP至G,使GP=DQ,易证△AGP≌△ADQ(SAS),则AG=AD,∠GAP=∠DAQ
由∠BAD=45°可得∠GAB=45°,则△GAB≌△BAD(SAS)∴BD=GB
s=S正方形APCQ-S△AGB=36-falseGB×AP=36-false×5×6=21
2.如图,在四边形AECD中,∠E=∠C=90°,AE=CE,M为EC上一点,若∠MAD=45°,CD=6,
CM=8,求EM的长.
解:延长CD,作AF⊥CD于点F,则四边形AECF为正方形
延长CF至B,使BF=ME,易证△AEM≌△AFB(SAS),则AM=AB,∠EAM=∠FAB
由∠BAD=45°,则∠EAM+∠DAF=45°
∴∠DAB=45°,则△MAD≌△BAD(SAS) ∴BD=MD=10
设EM=x ∴DF=10-x=8+x-6; x=4,即EM=4
3.如图,在正方形ABCD中,E为CD中点, ∠1=∠2.(1)求证:AE=45°(2)求false
(1)证明:过A作AM⊥EF ∵AB∥CD ∴∠AED=∠1
∵∠1=∠2 ∴∠AED=∠2 又∵AE=AE ∠D=∠AME=90°
∴△AEM≌△AED(AAS) ∴AM=AD ∠MAE=∠DAE
同理可证△ABF≌△AMF ∴∠BAF=∠FAM ∴∠FAE=false∠BAD=45°
(2)解:设正方形边长为2a BF=x ∵E为CD中点,∴DE=CE=a,CF=2a-x
由(1)知FE=BF+DE=a+x 在Rt△CEP中,由勾股定理得a2+(2a-x)2=(a+x)2
∴x=false∴false=false
4.如图,在正方形ABCD中,点E是AD上的一动点,连接BE.将△ABE沿直线BE折叠,A落在正方形ABCD形内的点F,直线CF交直线BE于P,求证:CF=falsePD
证明:作DQ⊥PC,BH⊥FC,易证△DQC≌△CHB ∴DQ=HC=HF
易证BH=HP=QC ∴PQ=HC=HF ∴PD=falsePQ=falseHC
而FC=2HC,∴?FC=falsePD
5.如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF=false,点G、H别为AB、CD边上的点,连接GH,若线段GH与EF的夹角为45°,求GH的长.
解:过B作BM//EF,BN//GH由题意得∠MBN=45
∴AM+CN=MN
又∵EF=false,AB=2,∴AM=1,设NC=x
∴DN=2-x,MN=x+1∴(x+1)2=(2-x)2+1,∴x=false
∴GH=BN=false
6.已知,正方形ABCD中,点M、N为AB、CD上的点,AP⊥M于E,交BC于P.
(1)如图1,求证:AP=MN;
(2)如图2,若EA=EF,连CF,点G为CF中点,连DG、DE,求证:DE=falseDG;
(3)在(2)的条件下,若DA=DE,且DN=false,BM=2,则DG=false.
证明:(1)作BF//MN,∴四边形MBFN为平行四边形∴MN=BF
可证△BFC≌△APB,∴BF=AP,∴AP=MN
(2)连EG并延长使得EG=QG,连CQ,∴CQ平行且等于EF
连DQ,可证∠DCQ=∠CNE=∠EAD且CQ=EF=AE
∴易证△DAE≌△DCQ,∴DE⊥DQ且DE=DQ
∴△DEG为等腰Rt△,∴DE=falseDG
7.点P为正方形ABCD外一点
(1)如图1,∠APB=45°,∠ABP=30°,求证:AB=falseAP
(2)如图2,PB平分∠APC,AE⊥BP,连DP,求证:PB+PD=2BE;
(3)如图3,AB=1,PA//BD,PB=BD,则PA=false;∠APB=30°
证明:(1)作AM⊥BP,设AM=a
AP=falsea,而AB=2a,∴AB=falseAP
(2)作BM⊥PC,BN⊥AP
∴BP平分∠APC,∴BN=BM,又∵BA=BC,∴△ABN≌△CBM,∴∠MAB=∠MCB
∴∠BAP+∠BCP=180°,∴∠ABC+∠APC=180°,∴∠APB=∠BPC=45°
作CQ⊥PC交PB的延长线于点Q,可证△PDC≌△QBC
∴∠Q=∠DPC=45°,∴PD+PB=falsePC
过C作CH⊥BP,可证CH=BE
又∵PC=falseHC,∴PC=falseBE,∴PB+PD=2BE
