第十八章 平行四边形章末复习:微专题4 菱形的综合训练(含答案)
文档属性
| 名称 | 第十八章 平行四边形章末复习:微专题4 菱形的综合训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 05:53:42 | ||
图片预览



文档简介
微专题4:菱形的综合训练
1.如图,已知P为边长为1的菱形ABCD对角线AC上一动点,M、N分别是AB、BC的中点,当P在AC上滑动时,则PM+PN最小值为( )
A. false B.1 C.2 D.无法确定
2.菱形ABCD的两条对角线AC、BD满足AB2=AC·BD,求菱形ABCD中的一个钝角的度数.
3.如图,菱形ABCD的周长为40,对角线AC=16
(1)求BD的长
(2)求菱形的高
4.如图,四边形ABCD与四边形AECF都是菱形,点E,F在BD上,∠EAF=30°,求false的值.
5.如图,Rt△ACB中,∠ ACB=90°,CD⊥AB,垂足为D点, AE平分∠CAB交CD于F点、交 BC于E点,FG∥BC ,交AB于G 点,求证:四边形CFGE为菱形.
6.如图,在菱形ABCD中,∠BAD=120°,E,F为BC和CD上一点,∠EAF=60°,探究BE,DF,AB之间的数量关系.
7.如图所示,在 Rt△ABC中,∠ABC=90°.将Rt△ABC绕点C顺时针方向旋转60°得到△DEC,点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF,连接AD.
(1)求证:四边形AFCD是菱形;
(2)连接BE并延长交AD于G,连接CG,请问:四边形ABCG是什么特殊平行四边形?为什么?
8.如图,E、F、G、H分别是矩形ABCD各边的中点
(1)求证:四边形FFGH为菱形
(2)若矩形ABCD的周长为falsecm,菱形EFGH的周长为8cm,求菱形EFGF的面积.
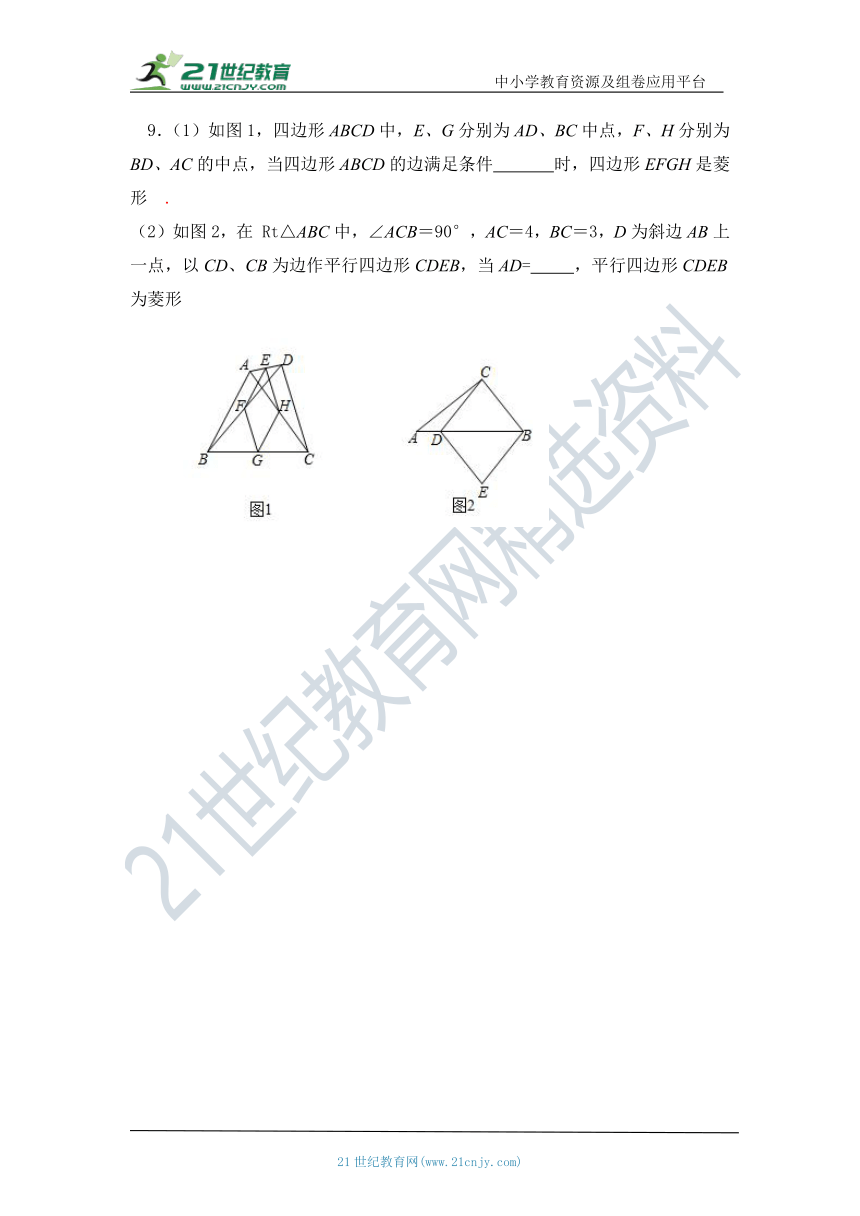
9.(1)如图1,四边形ABCD中,E、G分别为AD、BC中点,F、H分别为BD、AC的中点,当四边形ABCD的边满足条件 时,四边形EFGH是菱形 .
(2)如图2,在 Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= ,平行四边形CDEB为菱形
466725198755
231775055880
微专题4:菱形的综合训练
1.如图,已知P为边长为1的菱形ABCD对角线AC上一动点,M、N分别是AB、BC的中点,当P在AC上滑动时,则PM+PN最小值为( )
A. false B.1 C.2 D.无法确定
答案:B
2.菱形ABCD的两条对角线AC、BD满足AB2=AC·BD,求菱形ABCD中的一个钝角的度数.
答案:
解:设菱形ABCD的高为h,则 S菱形ABCD=falseAC?BD=AB?h=false AB2
∴AB=2h, ∴∠BAD=30°,∠ABC=150°
3.如图,菱形ABCD的周长为40,对角线AC=16
(1)求BD的长
(2)求菱形的高
答案:
解:(1)AD=false×40=10,AO=falseAC=8,AC⊥BD
∴DO2=AD2-AO2=36 ∴DO=6,∴BD=2DO=12
(2)∵ S菱形ABCD=falseAC?BD=AB?h ∴h= false
4.如图,四边形ABCD与四边形AECF都是菱形,点E,F在BD上,∠EAF=30°,求false的值.
答案:
解:连接AC,作EG⊥AB于G,易求∠BAC=60°,∠EAC=15° ∴∠BAE=45°
又∵∠ABD=30°,设AG=EG=x,则AE=false x,BG=false x, false
5.如图,Rt△ACB中,∠ ACB=90°,CD⊥AB,垂足为D点, AE平分∠CAB交CD于F点、交 BC于E点,FG∥BC ,交AB于G 点,求证:四边形CFGE为菱形.
答案:
证明:∵AE平分∠CAB ,∴ ∠CAE=∠GAE ∵EC ⊥AC于C,且EG⊥AB于G ∴EC=EG
∵CD⊥AB于D, ∠CEA+∠CAE=90° ∠ AFD+∠FAD=90°
∴∠CEF=∠AFD ∵∠ CFE =∠AFD ∴∠CEF=∠CFE ∴ CE=CF ∴ CF=EG
又∵CF∥EG, ∴四边形CFGE是平行四边形 又∵CF=CE,∴四边形CFGE是菱形
6.如图,在菱形ABCD中,∠BAD=120°,E,F为BC和CD上一点,∠EAF=60°,探究BE,DF,AB之间的数量关系.
答案:
解:连接AC,证△AEC≌△AFD ∴CE=DF. ∴BE+ DF=BE+CE=BC=AB
7.如图所示,在 Rt△ABC中,∠ABC=90°.将Rt△ABC绕点C顺时针方向旋转60°得到△DEC,点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF,连接AD.
(1)求证:四边形AFCD是菱形;
(2)连接BE并延长交AD于G,连接CG,请问:四边形ABCG是什么特殊平行四边形?为什么?
答案:
(1)证明:由△ABC旋转60°得△DEC可知∠ACB=60° 由△ABC绕AB翻转得△ABF
∴△AFC是等边三角形 ∴AF=FC=AC=CD ∴AF∥CD ,AF=CD
∴四边形AFCD是平行四边形 又∵AF=FC∴□AFCD是菱形
(2)解:由(1)知∠ACB=60° ∠BAC=30° ∴BC=CE=falseAC=AE
AG∥BC ∴△AGE≌△CBE ,∴AG∥BC,且AG=BC,
∴四边形ABCG是平行四边形 又∵∠ABC=90°∴□ ABCG是矩形
8.如图,E、F、G、H分别是矩形ABCD各边的中点
(1)求证:四边形FFGH为菱形
(2)若矩形ABCD的周长为falsecm,菱形EFGH的周长为8cm,求菱形EFGF的面积.
答案:
(1)证明:连接AC、BD ∵E、F、G、H分别为矩形ABCD各边的中点
∴EF∥HG∥BD, EF=HG=falseBD, ∴FG∥EH∥AC , GF=EH=falseAC
∴四边形EFGH为平行四边形 又∵AC=BD,∴EF=FG∴四边形EFGH为菱形
(2)解:∵EF=FG=GH=EH=false×8=2,EG=AB,FH=BC
∴EG+FH=false 又∵EG2+FH2=4EF2=16∴EG?FH=4,∴S菱形EFGH=falseEG?FH=2
9.(1)如图1,四边形ABCD中,E、G分别为AD、BC中点,F、H分别为BD、AC的中点,当四边形ABCD的边满足条件 时,四边形EFGH是菱形 .
(2)如图2,在 Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= ,平行四边形CDEB为菱形
466725198755
231775055880
答案:(1)AB=CD (2)75
1.如图,已知P为边长为1的菱形ABCD对角线AC上一动点,M、N分别是AB、BC的中点,当P在AC上滑动时,则PM+PN最小值为( )
A. false B.1 C.2 D.无法确定
2.菱形ABCD的两条对角线AC、BD满足AB2=AC·BD,求菱形ABCD中的一个钝角的度数.
3.如图,菱形ABCD的周长为40,对角线AC=16
(1)求BD的长
(2)求菱形的高
4.如图,四边形ABCD与四边形AECF都是菱形,点E,F在BD上,∠EAF=30°,求false的值.
5.如图,Rt△ACB中,∠ ACB=90°,CD⊥AB,垂足为D点, AE平分∠CAB交CD于F点、交 BC于E点,FG∥BC ,交AB于G 点,求证:四边形CFGE为菱形.
6.如图,在菱形ABCD中,∠BAD=120°,E,F为BC和CD上一点,∠EAF=60°,探究BE,DF,AB之间的数量关系.
7.如图所示,在 Rt△ABC中,∠ABC=90°.将Rt△ABC绕点C顺时针方向旋转60°得到△DEC,点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF,连接AD.
(1)求证:四边形AFCD是菱形;
(2)连接BE并延长交AD于G,连接CG,请问:四边形ABCG是什么特殊平行四边形?为什么?
8.如图,E、F、G、H分别是矩形ABCD各边的中点
(1)求证:四边形FFGH为菱形
(2)若矩形ABCD的周长为falsecm,菱形EFGH的周长为8cm,求菱形EFGF的面积.
9.(1)如图1,四边形ABCD中,E、G分别为AD、BC中点,F、H分别为BD、AC的中点,当四边形ABCD的边满足条件 时,四边形EFGH是菱形 .
(2)如图2,在 Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= ,平行四边形CDEB为菱形
466725198755
231775055880
微专题4:菱形的综合训练
1.如图,已知P为边长为1的菱形ABCD对角线AC上一动点,M、N分别是AB、BC的中点,当P在AC上滑动时,则PM+PN最小值为( )
A. false B.1 C.2 D.无法确定
答案:B
2.菱形ABCD的两条对角线AC、BD满足AB2=AC·BD,求菱形ABCD中的一个钝角的度数.
答案:
解:设菱形ABCD的高为h,则 S菱形ABCD=falseAC?BD=AB?h=false AB2
∴AB=2h, ∴∠BAD=30°,∠ABC=150°
3.如图,菱形ABCD的周长为40,对角线AC=16
(1)求BD的长
(2)求菱形的高
答案:
解:(1)AD=false×40=10,AO=falseAC=8,AC⊥BD
∴DO2=AD2-AO2=36 ∴DO=6,∴BD=2DO=12
(2)∵ S菱形ABCD=falseAC?BD=AB?h ∴h= false
4.如图,四边形ABCD与四边形AECF都是菱形,点E,F在BD上,∠EAF=30°,求false的值.
答案:
解:连接AC,作EG⊥AB于G,易求∠BAC=60°,∠EAC=15° ∴∠BAE=45°
又∵∠ABD=30°,设AG=EG=x,则AE=false x,BG=false x, false
5.如图,Rt△ACB中,∠ ACB=90°,CD⊥AB,垂足为D点, AE平分∠CAB交CD于F点、交 BC于E点,FG∥BC ,交AB于G 点,求证:四边形CFGE为菱形.
答案:
证明:∵AE平分∠CAB ,∴ ∠CAE=∠GAE ∵EC ⊥AC于C,且EG⊥AB于G ∴EC=EG
∵CD⊥AB于D, ∠CEA+∠CAE=90° ∠ AFD+∠FAD=90°
∴∠CEF=∠AFD ∵∠ CFE =∠AFD ∴∠CEF=∠CFE ∴ CE=CF ∴ CF=EG
又∵CF∥EG, ∴四边形CFGE是平行四边形 又∵CF=CE,∴四边形CFGE是菱形
6.如图,在菱形ABCD中,∠BAD=120°,E,F为BC和CD上一点,∠EAF=60°,探究BE,DF,AB之间的数量关系.
答案:
解:连接AC,证△AEC≌△AFD ∴CE=DF. ∴BE+ DF=BE+CE=BC=AB
7.如图所示,在 Rt△ABC中,∠ABC=90°.将Rt△ABC绕点C顺时针方向旋转60°得到△DEC,点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF,连接AD.
(1)求证:四边形AFCD是菱形;
(2)连接BE并延长交AD于G,连接CG,请问:四边形ABCG是什么特殊平行四边形?为什么?
答案:
(1)证明:由△ABC旋转60°得△DEC可知∠ACB=60° 由△ABC绕AB翻转得△ABF
∴△AFC是等边三角形 ∴AF=FC=AC=CD ∴AF∥CD ,AF=CD
∴四边形AFCD是平行四边形 又∵AF=FC∴□AFCD是菱形
(2)解:由(1)知∠ACB=60° ∠BAC=30° ∴BC=CE=falseAC=AE
AG∥BC ∴△AGE≌△CBE ,∴AG∥BC,且AG=BC,
∴四边形ABCG是平行四边形 又∵∠ABC=90°∴□ ABCG是矩形
8.如图,E、F、G、H分别是矩形ABCD各边的中点
(1)求证:四边形FFGH为菱形
(2)若矩形ABCD的周长为falsecm,菱形EFGH的周长为8cm,求菱形EFGF的面积.
答案:
(1)证明:连接AC、BD ∵E、F、G、H分别为矩形ABCD各边的中点
∴EF∥HG∥BD, EF=HG=falseBD, ∴FG∥EH∥AC , GF=EH=falseAC
∴四边形EFGH为平行四边形 又∵AC=BD,∴EF=FG∴四边形EFGH为菱形
(2)解:∵EF=FG=GH=EH=false×8=2,EG=AB,FH=BC
∴EG+FH=false 又∵EG2+FH2=4EF2=16∴EG?FH=4,∴S菱形EFGH=falseEG?FH=2
9.(1)如图1,四边形ABCD中,E、G分别为AD、BC中点,F、H分别为BD、AC的中点,当四边形ABCD的边满足条件 时,四边形EFGH是菱形 .
(2)如图2,在 Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= ,平行四边形CDEB为菱形
466725198755
231775055880
答案:(1)AB=CD (2)75
