第十八章 平行四边形章末复习:微专题5 正方形的综合训练(含答案)
文档属性
| 名称 | 第十八章 平行四边形章末复习:微专题5 正方形的综合训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 140.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 05:54:57 | ||
图片预览


文档简介
微专题5 正方形的综合训练
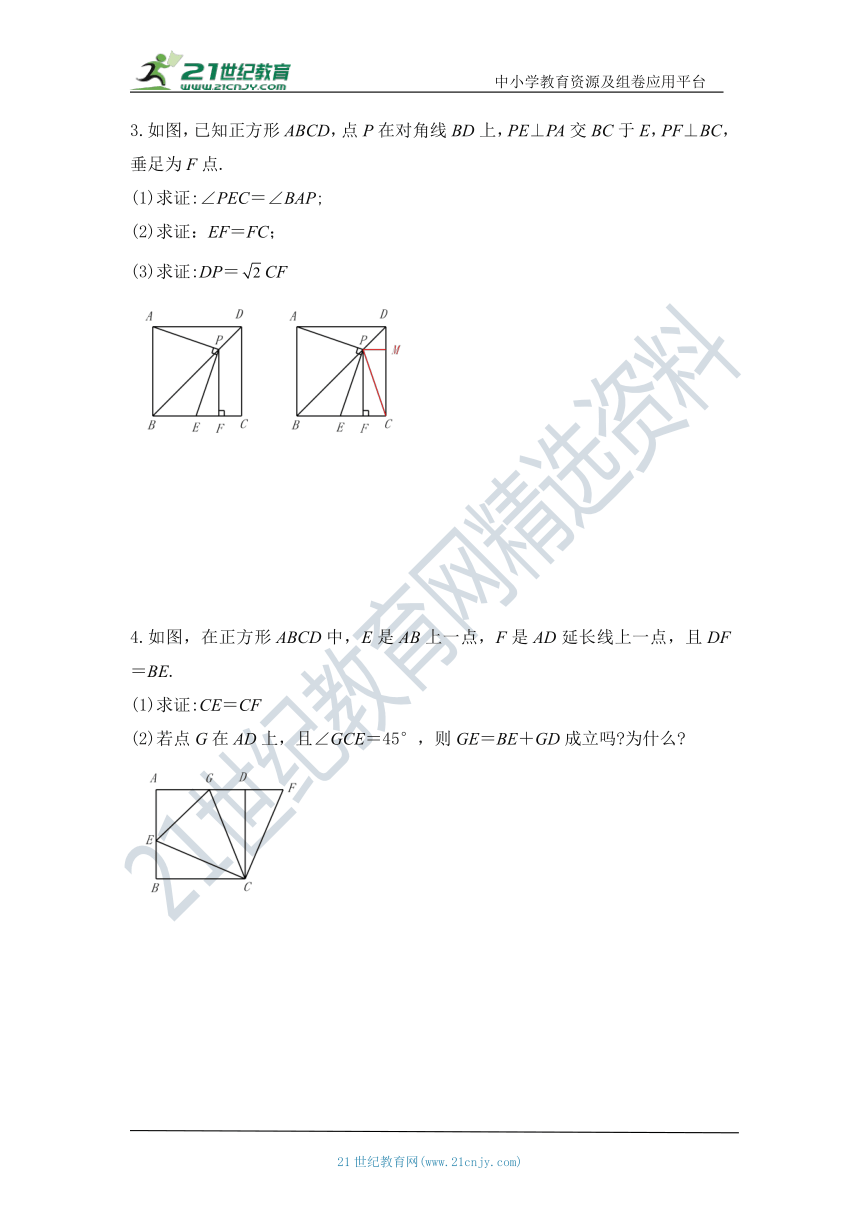
如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E
(1)求∠DEA的度数;
(2)若BD=2,求BE的长
2.如图1,在正方形ABCD中,E,F分别是AD,DC上的点,AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,且MP⊥NQ,MP与NQ是否相等?并说明理由.
图1 图2
3.如图,已知正方形ABCD,点P在对角线BD上,PE⊥PA交BC于E,PF⊥BC,垂足为F点.
(1)求证:∠PEC=∠BAP;
(2)求证:EF=FC;
(3)求证:DP=falseCF
4.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
5.如图,正方形ABCD中,P是对角线AC上一点,PE⊥PB交CD于E.
(1)写出PB、PE之间的数量关系并证明;
(2)写出PA、DE之间的数量关系并证明;
(3)写出CB、CE、CP之间的数量关系并证明:
(4)写出PA、PC、CE之间的数量关系并证明.
6.正方形ABCD中,点E在BC上,点F在AB上,且AF=BE,DF交AE于H.
(1)直接写出线段AE、DF的位置及数量关系为
(2)如图1,在HD上取一点M,使HM=HA,点O为MC的中点,请写出线段DH与DO的数量关系,并证明;
(3)如图2,将直线FD沿射线AE方向平移,交线段AB于M,交AE于I,交CD于K,是否存在DI=DC?若存在,求false的值:若不存在,请说明理由
微专题5 正方形的综合训练
1.如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E
(1)求∠DEA的度数;
(2)若BD=2,求BE的长
解:(1)∠DEA=∠ABE+∠BAE=67.5°
(2)可证∠DAE=∠DEA=67.5°∴DE=DA=false ∴BE=2-false
2.如图1,在正方形ABCD中,E,F分别是AD,DC上的点,AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,且MP⊥NQ,MP与NQ是否相等?并说明理由.
(1)证明:证△ABE≌△DAF
(2)解:相等,作MF⊥CD于F,作QE⊥BC于E,证△MPF≌△QNE即可
图1 图2
3.如图,已知正方形ABCD,点P在对角线BD上,PE⊥PA交BC于E,PF⊥BC,垂足为F点.
(1)求证:∠PEC=∠BAP;
(2)求证:EF=FC;
(3)求证:DP=falseCF
证明:(1)∵∠PEC+∠PEB=180°=∠BAP+∠BEP
∴∠PEC=∠BAP
(2)连PC,证△APB≌△CPB,PA=PC,∠BCP=∠BAP=∠PEC
PC=PE,∵PF⊥CE∴EF=CF
(3)作PM⊥CD于M,证DP=falsePM=falseCF
4.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(1)证明:∵四边形ABCD是正方形
BC=CD,∠B=∠CDF=90°
又∵BE=DF ∴△CBE≌△CDF(SAS) ∴CE=CF
(2)解:GE=BE+GD成立,理由:
由(1)得△CBE≌△CDF
∴∠BCE=∠DCF ∴∠BCE+∠ECD=∠DCF+∠ECD
即∠BCD=∠ECF=90°
又∵∠GCE=45° ∴∠GCF=∠GCE=45°
∵CE=CF,∠GCE=∠GCF,GC=GC
∴△ECG≌△FCG(SAS) ∴GE=GF ∴GE=DF+GD=BE+GD
5.如图,正方形ABCD中,P是对角线AC上一点,PE⊥PB交CD于E.
(1)写出PB、PE之间的数量关系并证明;
(2)写出PA、DE之间的数量关系并证明;
(3)写出CB、CE、CP之间的数量关系并证明:
(4)写出PA、PC、CE之间的数量关系并证明.
答案:(1)PB=PE 过P作MN∥BC,可证△MPB≌△NEP(ASA)
(2)由(1)知AM=DN=NE=falsePA ∴DE=falsePA
(3)由(2)知BC-CE=DE=falsePA=false(AC-CP)
又∵AC=falseBC ∴BC-CE=false(falseBC-CP) ∴BC+CE=falseCP
(4)PA+PC=AC=falseCD,CD-CE=DE=falseAP
(PA+PC)·false-CE=falsePA ∴false(PC-PA)=2CE 即PC-PA=falseCE
6.正方形ABCD中,点E在BC上,点F在AB上,且AF=BE,DF交AE于H.
(1)直接写出线段AE、DF的位置及数量关系为
(2)如图1,在HD上取一点M,使HM=HA,点O为MC的中点,请写出线段DH与DO的数量关系,并证明;
(3)如图2,将直线FD沿射线AE方向平移,交线段AB于M,交AE于I,交CD于K,是否存在DI=DC?若存在,求false的值:若不存在,请说明理由
解:(1)AE⊥DF,AE=DF
(2)DH=falseDO
连接HO并延长至点H,使OH1=OH,连接CH1、DH1
可得△HOM≌△H1OC ∴CH1=HM=AH,∠MHO=∠CH1O ∴DH∥CH1
又∠HAD+∠ADH=∠ADH+∠HDC=90°
即∠DAH=∠HDC=∠H1CD
又AD=DC ∴△HAD≌△H1CD, ∴∠ADH=∠CDH1,DH=H1D
∵∠HDH1=∠HDC+∠CDH1=∠HDC+∠ADH=90°
又OH=OH1 ∴DO⊥HO,∠HDO=45即DH=falseDO
(3)DI=DC=DA
作DD1⊥AE交AB于N1,连接N1I,则DD1∥NK,AD1=D1I
即得□DKMN1,NA=N1I;∴DK=NN1,AN1=N1I=NN1,∴false=2
如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E
(1)求∠DEA的度数;
(2)若BD=2,求BE的长
2.如图1,在正方形ABCD中,E,F分别是AD,DC上的点,AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,且MP⊥NQ,MP与NQ是否相等?并说明理由.
图1 图2
3.如图,已知正方形ABCD,点P在对角线BD上,PE⊥PA交BC于E,PF⊥BC,垂足为F点.
(1)求证:∠PEC=∠BAP;
(2)求证:EF=FC;
(3)求证:DP=falseCF
4.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
5.如图,正方形ABCD中,P是对角线AC上一点,PE⊥PB交CD于E.
(1)写出PB、PE之间的数量关系并证明;
(2)写出PA、DE之间的数量关系并证明;
(3)写出CB、CE、CP之间的数量关系并证明:
(4)写出PA、PC、CE之间的数量关系并证明.
6.正方形ABCD中,点E在BC上,点F在AB上,且AF=BE,DF交AE于H.
(1)直接写出线段AE、DF的位置及数量关系为
(2)如图1,在HD上取一点M,使HM=HA,点O为MC的中点,请写出线段DH与DO的数量关系,并证明;
(3)如图2,将直线FD沿射线AE方向平移,交线段AB于M,交AE于I,交CD于K,是否存在DI=DC?若存在,求false的值:若不存在,请说明理由
微专题5 正方形的综合训练
1.如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E
(1)求∠DEA的度数;
(2)若BD=2,求BE的长
解:(1)∠DEA=∠ABE+∠BAE=67.5°
(2)可证∠DAE=∠DEA=67.5°∴DE=DA=false ∴BE=2-false
2.如图1,在正方形ABCD中,E,F分别是AD,DC上的点,AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,且MP⊥NQ,MP与NQ是否相等?并说明理由.
(1)证明:证△ABE≌△DAF
(2)解:相等,作MF⊥CD于F,作QE⊥BC于E,证△MPF≌△QNE即可
图1 图2
3.如图,已知正方形ABCD,点P在对角线BD上,PE⊥PA交BC于E,PF⊥BC,垂足为F点.
(1)求证:∠PEC=∠BAP;
(2)求证:EF=FC;
(3)求证:DP=falseCF
证明:(1)∵∠PEC+∠PEB=180°=∠BAP+∠BEP
∴∠PEC=∠BAP
(2)连PC,证△APB≌△CPB,PA=PC,∠BCP=∠BAP=∠PEC
PC=PE,∵PF⊥CE∴EF=CF
(3)作PM⊥CD于M,证DP=falsePM=falseCF
4.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(1)证明:∵四边形ABCD是正方形
BC=CD,∠B=∠CDF=90°
又∵BE=DF ∴△CBE≌△CDF(SAS) ∴CE=CF
(2)解:GE=BE+GD成立,理由:
由(1)得△CBE≌△CDF
∴∠BCE=∠DCF ∴∠BCE+∠ECD=∠DCF+∠ECD
即∠BCD=∠ECF=90°
又∵∠GCE=45° ∴∠GCF=∠GCE=45°
∵CE=CF,∠GCE=∠GCF,GC=GC
∴△ECG≌△FCG(SAS) ∴GE=GF ∴GE=DF+GD=BE+GD
5.如图,正方形ABCD中,P是对角线AC上一点,PE⊥PB交CD于E.
(1)写出PB、PE之间的数量关系并证明;
(2)写出PA、DE之间的数量关系并证明;
(3)写出CB、CE、CP之间的数量关系并证明:
(4)写出PA、PC、CE之间的数量关系并证明.
答案:(1)PB=PE 过P作MN∥BC,可证△MPB≌△NEP(ASA)
(2)由(1)知AM=DN=NE=falsePA ∴DE=falsePA
(3)由(2)知BC-CE=DE=falsePA=false(AC-CP)
又∵AC=falseBC ∴BC-CE=false(falseBC-CP) ∴BC+CE=falseCP
(4)PA+PC=AC=falseCD,CD-CE=DE=falseAP
(PA+PC)·false-CE=falsePA ∴false(PC-PA)=2CE 即PC-PA=falseCE
6.正方形ABCD中,点E在BC上,点F在AB上,且AF=BE,DF交AE于H.
(1)直接写出线段AE、DF的位置及数量关系为
(2)如图1,在HD上取一点M,使HM=HA,点O为MC的中点,请写出线段DH与DO的数量关系,并证明;
(3)如图2,将直线FD沿射线AE方向平移,交线段AB于M,交AE于I,交CD于K,是否存在DI=DC?若存在,求false的值:若不存在,请说明理由
解:(1)AE⊥DF,AE=DF
(2)DH=falseDO
连接HO并延长至点H,使OH1=OH,连接CH1、DH1
可得△HOM≌△H1OC ∴CH1=HM=AH,∠MHO=∠CH1O ∴DH∥CH1
又∠HAD+∠ADH=∠ADH+∠HDC=90°
即∠DAH=∠HDC=∠H1CD
又AD=DC ∴△HAD≌△H1CD, ∴∠ADH=∠CDH1,DH=H1D
∵∠HDH1=∠HDC+∠CDH1=∠HDC+∠ADH=90°
又OH=OH1 ∴DO⊥HO,∠HDO=45即DH=falseDO
(3)DI=DC=DA
作DD1⊥AE交AB于N1,连接N1I,则DD1∥NK,AD1=D1I
即得□DKMN1,NA=N1I;∴DK=NN1,AN1=N1I=NN1,∴false=2
