第十八章 平行四边形章末复习:微专题8 正方形中的有关计算(选用)(含答案)
文档属性
| 名称 | 第十八章 平行四边形章末复习:微专题8 正方形中的有关计算(选用)(含答案) | 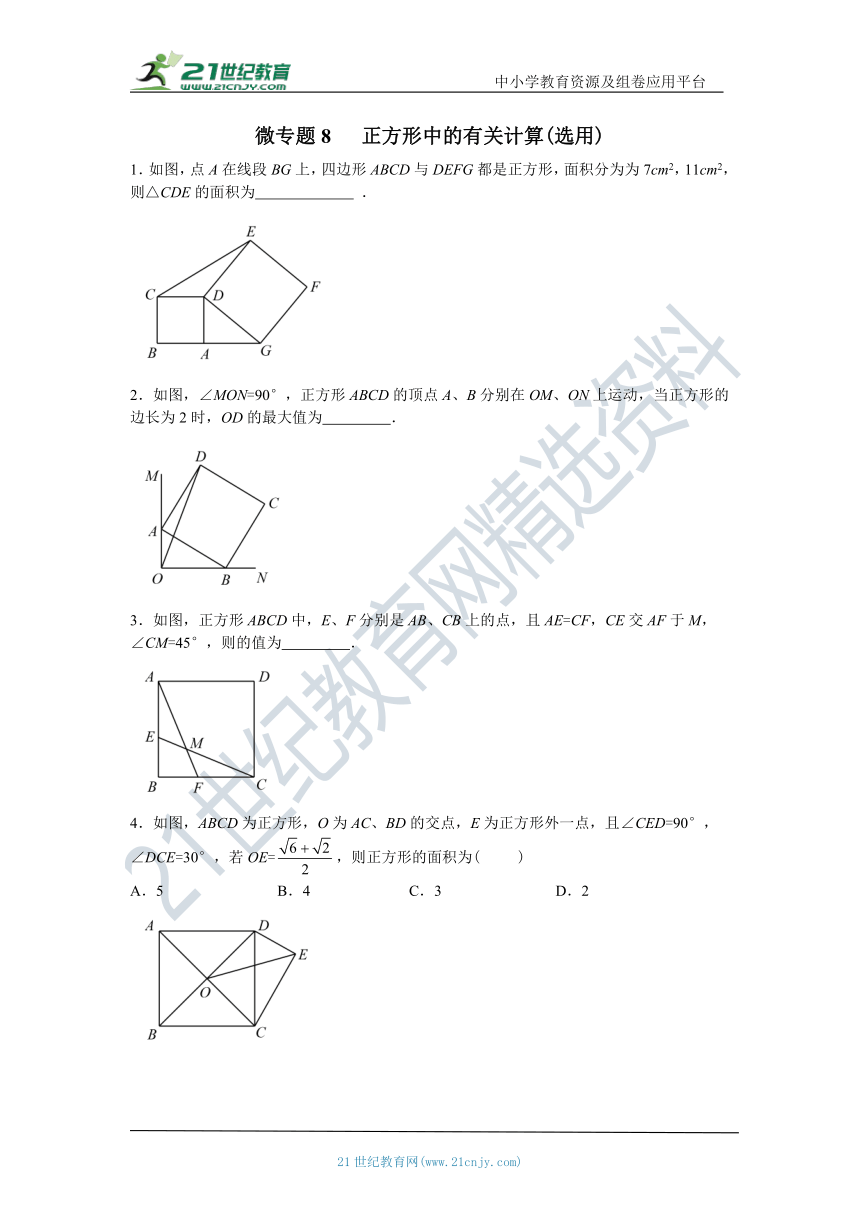 | |
| 格式 | docx | ||
| 文件大小 | 159.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 05:58:27 | ||
图片预览



文档简介
微专题8 正方形中的有关计算(选用)
1.如图,点A在线段BG上,四边形ABCD与DEFG都是正方形,面积分为为7cm2,11cm2,则△CDE的面积为 .
2.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上运动,当正方形的边长为2时,OD的最大值为 .
3.如图,正方形ABCD中,E、F分别是AB、CB上的点,且AE=CF,CE交AF于M,∠CM=45°,则的值为 .
4.如图,ABCD为正方形,O为AC、BD的交点,E为正方形外一点,且∠CED=90°,∠DCE=30°,若OE=false,则正方形的面积为( )
A.5 B.4 C.3 D.2
5.如图,正方形ABCD的对角线上有一条运动的线段MN,满足AB=falseMN,连接AN、CM,若AB=6,则当AN+CM为最小值时,线段AN的长度为 .
6.如图,正方形ABCD的边长为3,E,F分别是AB,CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到BCFE,C的对应点C’在AD边上,B’C’交AB于点G,求GE的长
7.在正方形ABCD中,点E是对角线BD上一动点,点F是射线AD上一动点,且EF=EC,点G为BF的中点
(1)如图1,求证:EG⊥AD;
(2)如图2,当点E在BD上,点F是射线AD上一动点,问false的值是否发生变化?若不变,求其值:若变化,请说明理由;
(3)若BE=falseEG=false,则BF的长为2
8.如图,在正方形ABCD中,P为AB上一点,PC的垂直平分线EF分别交AD、BC、BD、PC于E、F、M、N
(1)求证:EF=CP;
(2)求false的值
(3)求false的值;
(4)BG、MG、MD三条线段之间有何数量关系?请写出关系式并证明;
(5)若AP=2PB,求false的值
微专题8 正方形中的有关计算(选用)
1.如图,点A在线段BG上,四边形ABCD与DEFG都是正方形,面积分为为7cm2,11cm2,则△CDE的面积为false.
2.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上运动,当正方形的边长为2时,OD的最大值为1+false.
3.如图,正方形ABCD中,E、F分别是AB、CB上的点,且AE=CF,CE交AF于M,∠CM=45°,则的值为false+1.
4.如图,ABCD为正方形,O为AC、BD的交点,E为正方形外一点,且∠CED=90°,∠DCE=30°,若OE=false,则正方形的面积为( B )
A.5 B.4 C.3 D.2
5.如图,正方形ABCD的对角线上有一条运动的线段MN,满足AB=falseMN,连接AN、CM,若AB=6,则当AN+CM为最小值时,线段AN的长度为false.
6.如图,正方形ABCD的边长为3,E,F分别是AB,CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到BCFE,C的对应点C’在AD边上,B’C’交AB于点G,求GE的长
解:∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D,AB=AD=3
由折叠的性质得:FC’=FC,∠C’FE=∠CFE=60°,∠FC’B’=∠C=90°,
B’E=BE,∠B’=∠B=90°
∴∠DFC’=60°,∴∠DC’F=30°,FC’=FC=2DF
∵DF+CF=CD=3,∴DF+2DF=3,解得DF=1
∴DC’=falseDF=false,则CA=3-false,AG=3(3-false)
设EB=x,∵∠B’GE=∠AGC’=∠DC’F=30°,∴GE=2x
则false(3-false)+3x=3解得x=2-false,GE=4-2false
7.在正方形ABCD中,点E是对角线BD上一动点,点F是射线AD上一动点,且EF=EC,点G为BF的中点
(1)如图1,求证:EG⊥AD;
(2)如图2,当点E在BD上,点F是射线AD上一动点,问false的值是否发生变化?若不变,求其值:若变化,请说明理由;
(3)若BE=falseEG=false,则BF的长为2
(1)证明:过点E作AD的垂线交AD于点H,交BC于点,交BF于点G’
过点E作EJ⊥DC交DC于点J,则易证HE=EJ=IC
又∵EF=EC,∴△HEF≌△ICE,∴HF=EI
∴HF=BI=AH,∴H为AF的中点,∴HG’为△ABF的中位线
G’是BF的中点,∴G与G’重合,∴EG⊥AD
(2)解:false不变,为false
过点F作FH//CD交BD的延长线于点H,则 EG//FH且G为BF中点
∴EG=falseFH
又∵HF⊥AF且∠HDF=45°,DF=HF,∴false=false=false
8.如图,在正方形ABCD中,P为AB上一点,PC的垂直平分线EF分别交AD、BC、BD、PC于E、F、M、N
(1)求证:EF=CP;
(2)求false的值
(3)求false的值;
(4)BG、MG、MD三条线段之间有何数量关系?请写出关系式并证明;
(5)若AP=2PB,求false的值
(1)证明:过E作EQ⊥BC,垂足为Q
EQ⊥BC∴∠FEQ+∠QFN=90°
又∵PC⊥EF∴∠QFN+∠FCN=90°∠FEQ=∠FCN
又∵∠PBC=∠FQE=90°,BC=QE∴△PBC≌△FQE(AAS)∴CP=EF
(2)解:连接BN,则BN=PN=CN,∠NBF=∠NCF,∠MBN=45°-∠NBF
又∴∠MEQ+∠EMD+90°+45°=180°,∠EMD=45°-∠MEQ=45°-∠PCB=45°-∠NBF
∠MBN=∠EMD=∠BMF,∴false=false=false=false
(3)解:延长BC至H,使BP=CH,连接MP,MH,MC,∵PC的垂直平分线为EF,∴PM=MC
∴∠BPC+∠PBC+∠PCB+∠MPC=180+45°
∠BPC+∠MPC=135°-∠PCB,∠MCH=180°-∠PCB-∠PCM=135°-∠PCB
∴∠MCH=∠BPM∴△MPB≌△MCH,∴BM=MH,∠PMB=∠CMH,∴BM⊥MH
false=false=false
(4)解:连接AM,PM,MC,易证△AMB≌△CMB,∴CM=PM=AM,∴∠MAP=∠MPA
∵∠MPB+∠MPA=180°,∠MAP(∠MCB)+∠MPB=180°,∴∠PMC=90°,∴∠MCP=45°,
过C作CQ⊥CP且CQ=CG,连接DQ,MQ,∴△DQC≌△GCB,△GCM≌△QCM
∴DQ=BG,MG=QM,∠MDQ=90°MG2=BG2+MD2
(5)PB=1,AP=2, EA=x, ED=y.EP=EC.22+x2=32+y2,x2-y2=5,(x+y)(x-y)=5
∴x+y=3,∴x-y=false,∴false,∴false=false=false
1.如图,点A在线段BG上,四边形ABCD与DEFG都是正方形,面积分为为7cm2,11cm2,则△CDE的面积为 .
2.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上运动,当正方形的边长为2时,OD的最大值为 .
3.如图,正方形ABCD中,E、F分别是AB、CB上的点,且AE=CF,CE交AF于M,∠CM=45°,则的值为 .
4.如图,ABCD为正方形,O为AC、BD的交点,E为正方形外一点,且∠CED=90°,∠DCE=30°,若OE=false,则正方形的面积为( )
A.5 B.4 C.3 D.2
5.如图,正方形ABCD的对角线上有一条运动的线段MN,满足AB=falseMN,连接AN、CM,若AB=6,则当AN+CM为最小值时,线段AN的长度为 .
6.如图,正方形ABCD的边长为3,E,F分别是AB,CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到BCFE,C的对应点C’在AD边上,B’C’交AB于点G,求GE的长
7.在正方形ABCD中,点E是对角线BD上一动点,点F是射线AD上一动点,且EF=EC,点G为BF的中点
(1)如图1,求证:EG⊥AD;
(2)如图2,当点E在BD上,点F是射线AD上一动点,问false的值是否发生变化?若不变,求其值:若变化,请说明理由;
(3)若BE=falseEG=false,则BF的长为2
8.如图,在正方形ABCD中,P为AB上一点,PC的垂直平分线EF分别交AD、BC、BD、PC于E、F、M、N
(1)求证:EF=CP;
(2)求false的值
(3)求false的值;
(4)BG、MG、MD三条线段之间有何数量关系?请写出关系式并证明;
(5)若AP=2PB,求false的值
微专题8 正方形中的有关计算(选用)
1.如图,点A在线段BG上,四边形ABCD与DEFG都是正方形,面积分为为7cm2,11cm2,则△CDE的面积为false.
2.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上运动,当正方形的边长为2时,OD的最大值为1+false.
3.如图,正方形ABCD中,E、F分别是AB、CB上的点,且AE=CF,CE交AF于M,∠CM=45°,则的值为false+1.
4.如图,ABCD为正方形,O为AC、BD的交点,E为正方形外一点,且∠CED=90°,∠DCE=30°,若OE=false,则正方形的面积为( B )
A.5 B.4 C.3 D.2
5.如图,正方形ABCD的对角线上有一条运动的线段MN,满足AB=falseMN,连接AN、CM,若AB=6,则当AN+CM为最小值时,线段AN的长度为false.
6.如图,正方形ABCD的边长为3,E,F分别是AB,CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到BCFE,C的对应点C’在AD边上,B’C’交AB于点G,求GE的长
解:∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D,AB=AD=3
由折叠的性质得:FC’=FC,∠C’FE=∠CFE=60°,∠FC’B’=∠C=90°,
B’E=BE,∠B’=∠B=90°
∴∠DFC’=60°,∴∠DC’F=30°,FC’=FC=2DF
∵DF+CF=CD=3,∴DF+2DF=3,解得DF=1
∴DC’=falseDF=false,则CA=3-false,AG=3(3-false)
设EB=x,∵∠B’GE=∠AGC’=∠DC’F=30°,∴GE=2x
则false(3-false)+3x=3解得x=2-false,GE=4-2false
7.在正方形ABCD中,点E是对角线BD上一动点,点F是射线AD上一动点,且EF=EC,点G为BF的中点
(1)如图1,求证:EG⊥AD;
(2)如图2,当点E在BD上,点F是射线AD上一动点,问false的值是否发生变化?若不变,求其值:若变化,请说明理由;
(3)若BE=falseEG=false,则BF的长为2
(1)证明:过点E作AD的垂线交AD于点H,交BC于点,交BF于点G’
过点E作EJ⊥DC交DC于点J,则易证HE=EJ=IC
又∵EF=EC,∴△HEF≌△ICE,∴HF=EI
∴HF=BI=AH,∴H为AF的中点,∴HG’为△ABF的中位线
G’是BF的中点,∴G与G’重合,∴EG⊥AD
(2)解:false不变,为false
过点F作FH//CD交BD的延长线于点H,则 EG//FH且G为BF中点
∴EG=falseFH
又∵HF⊥AF且∠HDF=45°,DF=HF,∴false=false=false
8.如图,在正方形ABCD中,P为AB上一点,PC的垂直平分线EF分别交AD、BC、BD、PC于E、F、M、N
(1)求证:EF=CP;
(2)求false的值
(3)求false的值;
(4)BG、MG、MD三条线段之间有何数量关系?请写出关系式并证明;
(5)若AP=2PB,求false的值
(1)证明:过E作EQ⊥BC,垂足为Q
EQ⊥BC∴∠FEQ+∠QFN=90°
又∵PC⊥EF∴∠QFN+∠FCN=90°∠FEQ=∠FCN
又∵∠PBC=∠FQE=90°,BC=QE∴△PBC≌△FQE(AAS)∴CP=EF
(2)解:连接BN,则BN=PN=CN,∠NBF=∠NCF,∠MBN=45°-∠NBF
又∴∠MEQ+∠EMD+90°+45°=180°,∠EMD=45°-∠MEQ=45°-∠PCB=45°-∠NBF
∠MBN=∠EMD=∠BMF,∴false=false=false=false
(3)解:延长BC至H,使BP=CH,连接MP,MH,MC,∵PC的垂直平分线为EF,∴PM=MC
∴∠BPC+∠PBC+∠PCB+∠MPC=180+45°
∠BPC+∠MPC=135°-∠PCB,∠MCH=180°-∠PCB-∠PCM=135°-∠PCB
∴∠MCH=∠BPM∴△MPB≌△MCH,∴BM=MH,∠PMB=∠CMH,∴BM⊥MH
false=false=false
(4)解:连接AM,PM,MC,易证△AMB≌△CMB,∴CM=PM=AM,∴∠MAP=∠MPA
∵∠MPB+∠MPA=180°,∠MAP(∠MCB)+∠MPB=180°,∴∠PMC=90°,∴∠MCP=45°,
过C作CQ⊥CP且CQ=CG,连接DQ,MQ,∴△DQC≌△GCB,△GCM≌△QCM
∴DQ=BG,MG=QM,∠MDQ=90°MG2=BG2+MD2
(5)PB=1,AP=2, EA=x, ED=y.EP=EC.22+x2=32+y2,x2-y2=5,(x+y)(x-y)=5
∴x+y=3,∴x-y=false,∴false,∴false=false=false
