人教版2020--2021九年级(下)数学第二十七单元《相似》质量检测试卷A
文档属性
| 名称 | 人教版2020--2021九年级(下)数学第二十七单元《相似》质量检测试卷A |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 15:57:16 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2020-20201年九年级(下)第二十七章相似检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3
分,共30分)
1.
如图,在
中,,,
于点
,则
与
的周长之比为
A.
B.
C.
D.
2.
下列各组图形一定相似的是
A.
任意两个等腰三角形
B.
斜边和一条直角边对应成比例的两个直角三角形
C.
两条边成比例的两个直角三角形
D.
两条边之比为
的两个直角三角形
3.
下列四组线段中,是成比例线段的是
A.
,,,
B.
,,,
C.
,,,
D.
,,,
4.
若
,且面积比为
,则
与
的相似比为
A.
B.
C.
D.
5.
如图,,则下列关系式一定成立的是
A.
B.
C.
D.
6.
两个边数相同的多边形相似应具备的条件是
A.
各角对应相等
B.
各边对应成比例
C.
各角对应相等,各边对应相等
D.
各角对应相等,各边对应成比例
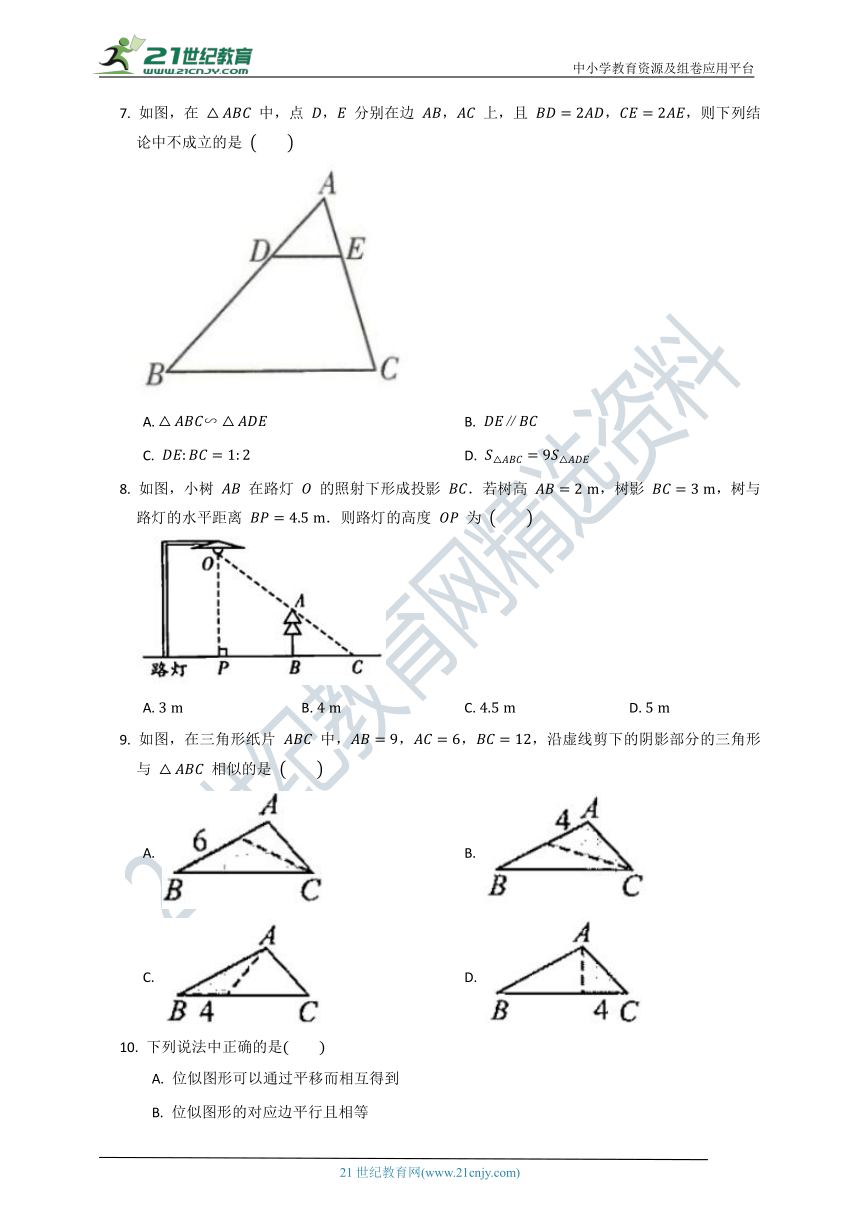
7.
如图,在
中,点
,
分别在边
,
上,且
,,则下列结论中不成立的是
A.
B.
C.
D.
8.
如图,小树
在路灯
的照射下形成投影
.若树高
,树影
,树与路灯的水平距离
.则路灯的高度
为
A.
B.
C.
D.
9.
如图,在三角形纸片
中,,,,沿虚线剪下的阴影部分的三角形与
相似的是
A.
B.
C.
D.
10.
下列说法中正确的是
A.
位似图形可以通过平移而相互得到
B.
位似图形的对应边平行且相等
C.
位似图形的位似中心不只有一个
D.
位似中心到对应点的距离之比都相等
二、填空题(共6小题;每小题3分,共18分)
11.
已知
,对应比的边为
,则:
相似比
?,对应高的比
?,
周长比
?,对应中线的比
?,
面积比
?,对应角平分线的比
?.
12.
已知
是
和
的比例中项,那么
?.
13.
如图,在
中,,点
在
上,且
,,则
?.
14.
在
内有边长分别为
,,
的三个正方形如图摆放,则中间的正方形的边长
的值为
?.
15.
在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图,请在边长为
个单位的
的方格纸中,找出一个格点三角形
.如果
与
相似(相似比不为
),那么
的面积为
?.
16.
如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点
,镜子
,树底
三点在同一水平线上,眼睛与地面的高度为
米,
米,
米,则树高为
?米.
三、解答题(共9小题;共72分)
17.(8分)
在如图所示的两个相似四边形中,求
,,
的值.
18.
(8分)如图,在
中,,,,点
从
出发,沿
方向以
的速度移动,点
从
出发,沿
方向以
的速度移动,若
,
分别同时从
,
出发,试探究经过多少秒后,以点
,,
为顶点的三角形与
相似?
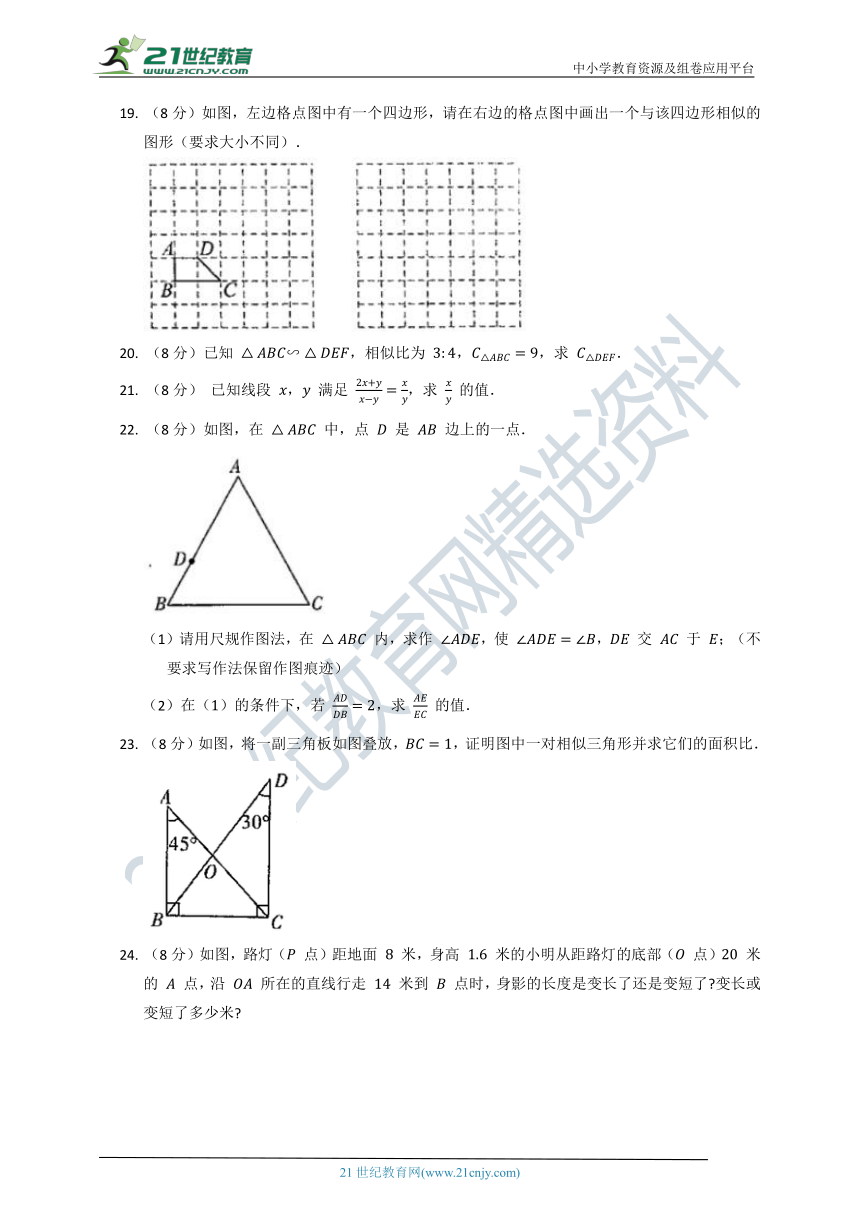
19.
(8分)如图,左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形(要求大小不同).
20.
(8分)已知
,相似比为
,,求
.
21.
(8分)
已知线段
,
满足
,求
的值.
22.
(8分)如图,在
中,点
是
边上的一点.
(1)请用尺规作图法,在
内,求作
,使
,
交
于
;(不要求写作法保留作图痕迹)
(2)在()的条件下,若
,求
的值.
23.
(8分)如图,将一副三角板如图叠放,,证明图中一对相似三角形并求它们的面积比.
24.
(8分)如图,路灯(
点)距地面
米,身高
米的小明从距路灯的底部(
点)
米的
点,沿
所在的直线行走
米到
点时,身影的长度是变长了还是变短了?变长或变短了多少米?
25.
(8分)在如图所示的方格纸中,
的顶点分别为
,,,
与
是以点
为位似中心的位似图形.
(1)在图中标出位似中心
的位置,并写出点
及点
的对应点
的坐标;
(2)以原点
为位似中心,在位似中心的同侧画出与
位似的
,使它与
的相似比为
,并写出点
的对应点
的坐标;
(3)
内部一点
的坐标为
,写出
在
中的对应点
的坐标.
答案
第一部分
1.
A
2.
B
3.
C
4.
C
5.
C
6.
D
7.
C
8.
D
9.
B
10.
D
【解析】【分析】位似是相似的特殊形式,根据性质可知,位似图形的对应边平行但不一定相等,位似图形的位似中心只有一个,平移图形是全等图形,也没有位似中心.位似中心到对应点的距离之比都相等,从而判断正确答案为.
【解析】解:位似是相似的特殊形式,
位似图形的对应边平行但不一定相等,
位似图形的位似中心只有一个,
平移图形是全等图形,也没有位似中心.
位似中心到对应点的距离之比都相等
正确答案为.
故选:.
【点评】本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比.
第二部分
11.
,,,,,
12.
13.
14.
【解析】如图,
在
中(),放置边长分别
,,
的三个正方形,
,
,
,,,
,,
,
(不符合题意,舍去),.
15.
【解析】如图.
,,,
.
,,,
.
.
.
.
16.
第三部分
17.
,,.
18.
设经过
秒后,两三角形相似,
①当
时,,
,,
②当
时,,
,,
经过
秒或
秒,以
,,
为顶点的三角形与
相似.
19.
如图所示,四边形
即为所求作.(答案不唯一)
20.
,
相似比为
,
,
.
21.
,
,
.
,
.
22.
(1)
如图,
为所作;
??????(2)
,
,
.
23.
.
证明如下:由
得
,
.
求相似比:
,
.
,,
.
.
与
的相似比
.
面积比
.
24.
,,
.
,即
.
解得
.
同样由
可求得
.
小明的身影变短了
米.
25.
(1)
点
的位置如图所示,点
的坐标为
,点
的坐标为
.
??????(2)
如图所示,
的坐标为
.
??????(3)
的坐标为
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
人教版2020-20201年九年级(下)第二十七章相似检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3
分,共30分)
1.
如图,在
中,,,
于点
,则
与
的周长之比为
A.
B.
C.
D.
2.
下列各组图形一定相似的是
A.
任意两个等腰三角形
B.
斜边和一条直角边对应成比例的两个直角三角形
C.
两条边成比例的两个直角三角形
D.
两条边之比为
的两个直角三角形
3.
下列四组线段中,是成比例线段的是
A.
,,,
B.
,,,
C.
,,,
D.
,,,
4.
若
,且面积比为
,则
与
的相似比为
A.
B.
C.
D.
5.
如图,,则下列关系式一定成立的是
A.
B.
C.
D.
6.
两个边数相同的多边形相似应具备的条件是
A.
各角对应相等
B.
各边对应成比例
C.
各角对应相等,各边对应相等
D.
各角对应相等,各边对应成比例
7.
如图,在
中,点
,
分别在边
,
上,且
,,则下列结论中不成立的是
A.
B.
C.
D.
8.
如图,小树
在路灯
的照射下形成投影
.若树高
,树影
,树与路灯的水平距离
.则路灯的高度
为
A.
B.
C.
D.
9.
如图,在三角形纸片
中,,,,沿虚线剪下的阴影部分的三角形与
相似的是
A.
B.
C.
D.
10.
下列说法中正确的是
A.
位似图形可以通过平移而相互得到
B.
位似图形的对应边平行且相等
C.
位似图形的位似中心不只有一个
D.
位似中心到对应点的距离之比都相等
二、填空题(共6小题;每小题3分,共18分)
11.
已知
,对应比的边为
,则:
相似比
?,对应高的比
?,
周长比
?,对应中线的比
?,
面积比
?,对应角平分线的比
?.
12.
已知
是
和
的比例中项,那么
?.
13.
如图,在
中,,点
在
上,且
,,则
?.
14.
在
内有边长分别为
,,
的三个正方形如图摆放,则中间的正方形的边长
的值为
?.
15.
在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图,请在边长为
个单位的
的方格纸中,找出一个格点三角形
.如果
与
相似(相似比不为
),那么
的面积为
?.
16.
如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点
,镜子
,树底
三点在同一水平线上,眼睛与地面的高度为
米,
米,
米,则树高为
?米.
三、解答题(共9小题;共72分)
17.(8分)
在如图所示的两个相似四边形中,求
,,
的值.
18.
(8分)如图,在
中,,,,点
从
出发,沿
方向以
的速度移动,点
从
出发,沿
方向以
的速度移动,若
,
分别同时从
,
出发,试探究经过多少秒后,以点
,,
为顶点的三角形与
相似?
19.
(8分)如图,左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形(要求大小不同).
20.
(8分)已知
,相似比为
,,求
.
21.
(8分)
已知线段
,
满足
,求
的值.
22.
(8分)如图,在
中,点
是
边上的一点.
(1)请用尺规作图法,在
内,求作
,使
,
交
于
;(不要求写作法保留作图痕迹)
(2)在()的条件下,若
,求
的值.
23.
(8分)如图,将一副三角板如图叠放,,证明图中一对相似三角形并求它们的面积比.
24.
(8分)如图,路灯(
点)距地面
米,身高
米的小明从距路灯的底部(
点)
米的
点,沿
所在的直线行走
米到
点时,身影的长度是变长了还是变短了?变长或变短了多少米?
25.
(8分)在如图所示的方格纸中,
的顶点分别为
,,,
与
是以点
为位似中心的位似图形.
(1)在图中标出位似中心
的位置,并写出点
及点
的对应点
的坐标;
(2)以原点
为位似中心,在位似中心的同侧画出与
位似的
,使它与
的相似比为
,并写出点
的对应点
的坐标;
(3)
内部一点
的坐标为
,写出
在
中的对应点
的坐标.
答案
第一部分
1.
A
2.
B
3.
C
4.
C
5.
C
6.
D
7.
C
8.
D
9.
B
10.
D
【解析】【分析】位似是相似的特殊形式,根据性质可知,位似图形的对应边平行但不一定相等,位似图形的位似中心只有一个,平移图形是全等图形,也没有位似中心.位似中心到对应点的距离之比都相等,从而判断正确答案为.
【解析】解:位似是相似的特殊形式,
位似图形的对应边平行但不一定相等,
位似图形的位似中心只有一个,
平移图形是全等图形,也没有位似中心.
位似中心到对应点的距离之比都相等
正确答案为.
故选:.
【点评】本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比.
第二部分
11.
,,,,,
12.
13.
14.
【解析】如图,
在
中(),放置边长分别
,,
的三个正方形,
,
,
,,,
,,
,
(不符合题意,舍去),.
15.
【解析】如图.
,,,
.
,,,
.
.
.
.
16.
第三部分
17.
,,.
18.
设经过
秒后,两三角形相似,
①当
时,,
,,
②当
时,,
,,
经过
秒或
秒,以
,,
为顶点的三角形与
相似.
19.
如图所示,四边形
即为所求作.(答案不唯一)
20.
,
相似比为
,
,
.
21.
,
,
.
,
.
22.
(1)
如图,
为所作;
??????(2)
,
,
.
23.
.
证明如下:由
得
,
.
求相似比:
,
.
,,
.
.
与
的相似比
.
面积比
.
24.
,,
.
,即
.
解得
.
同样由
可求得
.
小明的身影变短了
米.
25.
(1)
点
的位置如图所示,点
的坐标为
,点
的坐标为
.
??????(2)
如图所示,
的坐标为
.
??????(3)
的坐标为
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
