苏科版八年级下册数学 8.3频率与概率课件(25张ppt)
文档属性
| 名称 | 苏科版八年级下册数学 8.3频率与概率课件(25张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 00:00:00 | ||
图片预览







文档简介
苏科版八年级数学下册第八章
看一看:
明天下雨的可能性有多大?
买一张彩票中奖的可能性有多大?
抛掷1枚质地均匀的硬币,
正面朝上的可能性有多大?
抛掷1枚质地均匀的骰子,
向上一面的点数是6的可能性有多大?
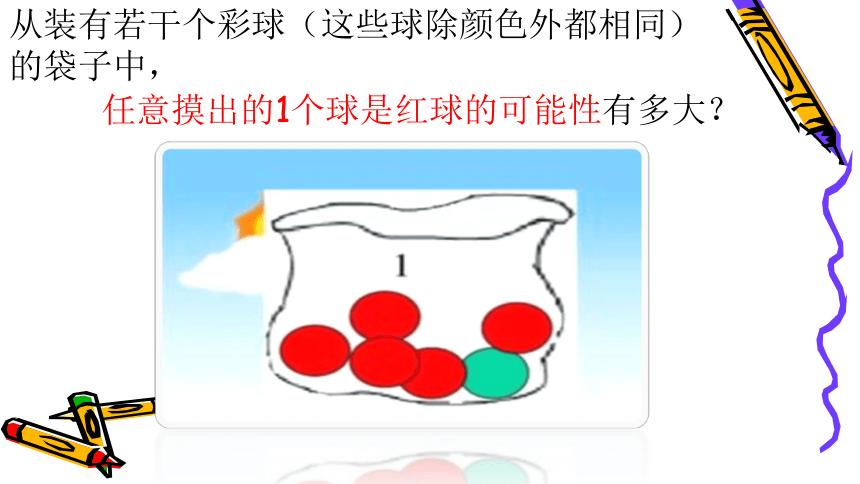
从装有若干个彩球(这些球除颜色外都相同)
的袋子中,
任意摸出的1个球是红球的可能性有多大?
郎朗、刘谦的手:《加油!向未来》的时候,因为节目设置中有高危动作,节目组给郎朗和刘谦特别投了手部的保险,保额高达300万元。
刘德华的脸:
拍摄电影《星梦奇缘》时,为脸投了3000万元的保险
罗纳尔多双腿:2600万美元
舒马赫的手臂:1500万美元
皇马守护神卡西利亚斯的双手:750万欧元
贝克汉姆右脚:1亿英镑
飞机失事会给旅客造成意外伤害.一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此保险公司必须精确计算出飞机失事的可能性有多大.
随机事件发生的可能性有大有小.
概率的含义
一个事件发生的可能性大小的数值,称为这个事件发生的概率。
表示:
P(A)表示事件A发生的概率
用字母A表示一个事件
活动一
1、一个不透明的袋子中装有10个黄球.
思考:
(1)摸到黄球的概率
(2)摸到白球的概率
2、一个不透明的袋子中装有6个黄球,4个白球.
P(摸到白球)
P(摸到黄球)
P(摸到白球)
0<
<1
P(摸到黄球)
0<
<1
必然事件
不可能事件
随机事件
是多少?
=1
=0
是多少?
摸到黄球,白球各自的概率是多少?
归纳:
必然事件A发生的概率是1,记作P(A)=1
不可能事件A发生的概率是0,记作P(A)=0
随机事件A发生的概率P(A)是0和1之间的一个数.
P(A)
0<
<1
练一练:
1、下列说法正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为0.5
C.概率很小的事件不可能发生
D.概率很大的事件一定会发生
A
练一练:
2、对“某市明天下雨的概率是75%”这句话,理解正确的是( )
A.某市明天将有75%的时间下雨
B.某市明天将有75%的地区下雨
C.某市明天一定下雨
D.某市明天下雨的可能性较大
D
归纳:
一个随机事件发生的概率是由这个随机事件自身决定的,并且是客观存在的.
概率是随机事件自身的属性,它反映这个随机事件发生的可能性大小.
一个随机事件的发生与不发生的概率不总是各占一半的
活动二:
做“抛掷质地均匀的硬币实验”,每人10次
记录每次结果:
抛掷结果
划记
频数
正面朝上
反面朝上
统计小组内各个组员抛掷硬币正面朝上的结果:
结果/组员号
1
2
3
4
5
正面朝上频数
1.分别汇总5人、10人、15人……的试验结果,并将试验数据汇总填入下表:
2.根据上表,画出折线统计图
3.观察所画的折线统计图,你发现了什么?
观察课本P45折线统计图,当抛掷硬币次数很大时,正面朝上的频率是否比较稳定?
下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据.
观察此表,你发现了什么?
从上表可以看出,当实验次数很大时,“正面朝上”的频率在0.5附近摆动.
练一练:
抽取的足球数
50
100
200
500
1000
2000
优等品的频数
46
93
192
472
953
1902
优等品的频率
某批足球质量检验结果
1、计算优等品的频率
2、画出优等品频率的折线统计图
3、当抽取的足球数很大时,优等品的频率会在哪个常数附近摆动?
练一练:
抽取的足球数
50
100
200
500
1000
2000
优等品的频数
46
93
192
472
953
1902
优等品的频率
0.92
0.93
0.97
0.944
0.953
0.952
某批足球质量检验结果
从上表可以看到,当抽查的足球数很多时,抽到优等品的频率接近于某一个常数,并在它附近摆动.
通常,在多次重复试验中,一个随机事件发生的频率会在某一个常数附近摆动,并且趋于稳定.这个性质称为频率的稳定性.
试一试:
1. 某地区从某年起几十年内的新生婴儿数及其中的男婴数如下:
时间范围
10年内
20年内
30年内
40年内
50年内
新生婴儿数
55 440
96 070
135 200
171 900
211 030
男婴出生的
频数
28 830
49 700
69 940
88 920
109160
男婴出生的
频率(0.001)
0.520
0.517
0.517
0.517
0.517
思考:你认为该地区男婴出生的频率稳定吗?它会在哪个常数附近摆动?
试一试:
2. 某篮球队员在罚球线上投篮的结果如下:
投篮次数
100
200
300
400
500
600
700
800
投中的频数
48
106
153
196
254
302
349
401
投中的频率
思考:当投篮次数很大时,你认为该篮球队员在罚球线上投篮投中的频率稳定吗?它会在哪个常数附近摆动?
试一试:
3. 某种水稻种子在相同条件下发芽实验的结果如下:
每批粒数
50
100
200
500
1000
2000
3000
5000
发芽的频数
47
89
188
460
890
1820
2730
4500
发芽的频率
思考:当实验次数很大时,你认为该种子发芽的频率稳定吗?它会在哪个常数附近摆动?
说一说:
你在这节课有哪些收获?
小结:
1、概率的含义及表示方法.
2、频率的稳定性
看一看:
明天下雨的可能性有多大?
买一张彩票中奖的可能性有多大?
抛掷1枚质地均匀的硬币,
正面朝上的可能性有多大?
抛掷1枚质地均匀的骰子,
向上一面的点数是6的可能性有多大?
从装有若干个彩球(这些球除颜色外都相同)
的袋子中,
任意摸出的1个球是红球的可能性有多大?
郎朗、刘谦的手:《加油!向未来》的时候,因为节目设置中有高危动作,节目组给郎朗和刘谦特别投了手部的保险,保额高达300万元。
刘德华的脸:
拍摄电影《星梦奇缘》时,为脸投了3000万元的保险
罗纳尔多双腿:2600万美元
舒马赫的手臂:1500万美元
皇马守护神卡西利亚斯的双手:750万欧元
贝克汉姆右脚:1亿英镑
飞机失事会给旅客造成意外伤害.一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此保险公司必须精确计算出飞机失事的可能性有多大.
随机事件发生的可能性有大有小.
概率的含义
一个事件发生的可能性大小的数值,称为这个事件发生的概率。
表示:
P(A)表示事件A发生的概率
用字母A表示一个事件
活动一
1、一个不透明的袋子中装有10个黄球.
思考:
(1)摸到黄球的概率
(2)摸到白球的概率
2、一个不透明的袋子中装有6个黄球,4个白球.
P(摸到白球)
P(摸到黄球)
P(摸到白球)
0<
<1
P(摸到黄球)
0<
<1
必然事件
不可能事件
随机事件
是多少?
=1
=0
是多少?
摸到黄球,白球各自的概率是多少?
归纳:
必然事件A发生的概率是1,记作P(A)=1
不可能事件A发生的概率是0,记作P(A)=0
随机事件A发生的概率P(A)是0和1之间的一个数.
P(A)
0<
<1
练一练:
1、下列说法正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为0.5
C.概率很小的事件不可能发生
D.概率很大的事件一定会发生
A
练一练:
2、对“某市明天下雨的概率是75%”这句话,理解正确的是( )
A.某市明天将有75%的时间下雨
B.某市明天将有75%的地区下雨
C.某市明天一定下雨
D.某市明天下雨的可能性较大
D
归纳:
一个随机事件发生的概率是由这个随机事件自身决定的,并且是客观存在的.
概率是随机事件自身的属性,它反映这个随机事件发生的可能性大小.
一个随机事件的发生与不发生的概率不总是各占一半的
活动二:
做“抛掷质地均匀的硬币实验”,每人10次
记录每次结果:
抛掷结果
划记
频数
正面朝上
反面朝上
统计小组内各个组员抛掷硬币正面朝上的结果:
结果/组员号
1
2
3
4
5
正面朝上频数
1.分别汇总5人、10人、15人……的试验结果,并将试验数据汇总填入下表:
2.根据上表,画出折线统计图
3.观察所画的折线统计图,你发现了什么?
观察课本P45折线统计图,当抛掷硬币次数很大时,正面朝上的频率是否比较稳定?
下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据.
观察此表,你发现了什么?
从上表可以看出,当实验次数很大时,“正面朝上”的频率在0.5附近摆动.
练一练:
抽取的足球数
50
100
200
500
1000
2000
优等品的频数
46
93
192
472
953
1902
优等品的频率
某批足球质量检验结果
1、计算优等品的频率
2、画出优等品频率的折线统计图
3、当抽取的足球数很大时,优等品的频率会在哪个常数附近摆动?
练一练:
抽取的足球数
50
100
200
500
1000
2000
优等品的频数
46
93
192
472
953
1902
优等品的频率
0.92
0.93
0.97
0.944
0.953
0.952
某批足球质量检验结果
从上表可以看到,当抽查的足球数很多时,抽到优等品的频率接近于某一个常数,并在它附近摆动.
通常,在多次重复试验中,一个随机事件发生的频率会在某一个常数附近摆动,并且趋于稳定.这个性质称为频率的稳定性.
试一试:
1. 某地区从某年起几十年内的新生婴儿数及其中的男婴数如下:
时间范围
10年内
20年内
30年内
40年内
50年内
新生婴儿数
55 440
96 070
135 200
171 900
211 030
男婴出生的
频数
28 830
49 700
69 940
88 920
109160
男婴出生的
频率(0.001)
0.520
0.517
0.517
0.517
0.517
思考:你认为该地区男婴出生的频率稳定吗?它会在哪个常数附近摆动?
试一试:
2. 某篮球队员在罚球线上投篮的结果如下:
投篮次数
100
200
300
400
500
600
700
800
投中的频数
48
106
153
196
254
302
349
401
投中的频率
思考:当投篮次数很大时,你认为该篮球队员在罚球线上投篮投中的频率稳定吗?它会在哪个常数附近摆动?
试一试:
3. 某种水稻种子在相同条件下发芽实验的结果如下:
每批粒数
50
100
200
500
1000
2000
3000
5000
发芽的频数
47
89
188
460
890
1820
2730
4500
发芽的频率
思考:当实验次数很大时,你认为该种子发芽的频率稳定吗?它会在哪个常数附近摆动?
说一说:
你在这节课有哪些收获?
小结:
1、概率的含义及表示方法.
2、频率的稳定性
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
