8.3.1 实际问题与二元一次方程组(1) 课件(共24张PPT)
文档属性
| 名称 | 8.3.1 实际问题与二元一次方程组(1) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 15:46:07 | ||
图片预览








文档简介
2021年春人教版七年级(下)数学
第八章 二元一次方程组
能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.
学会利用二元一次方程组解决典型实际问题.
学习目标
问题1:解二元一次方程组主要有哪几种方法?
问题2:列一元一次方程解决实际问题的步骤有哪些?
审、设、列、解、验、答
代入消元法和加减消元法
温故知新
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李大叔估计的准确吗?
新课导入
问题1:题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2:题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为xkg和ykg,
探究新知
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组:x= ,
y= .
20
5
随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人,则:
+ = 42,
+ = 20.
8x
5y
4x
2y
解得:
x =4
y = 2
答:李大叔应聘请甲种饲养员4人,乙种饲养员2人.
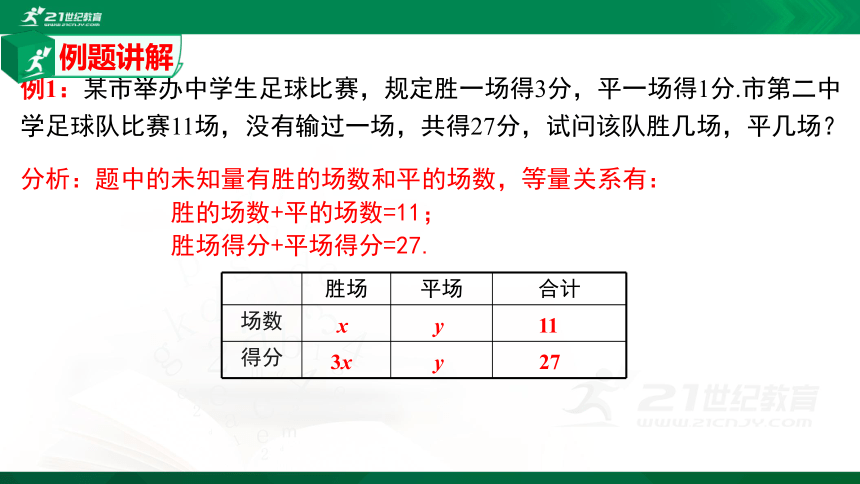
例1:某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场,平几场?
分析:题中的未知量有胜的场数和平的场数,等量关系有:
胜的场数+平的场数=11;
胜场得分+平场得分=27.
胜场
平场
合计
场数
得分
x
3x
y
y
11
27
例题讲解
解:设市第二中学足球队胜x场,平y场.依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场,平3场.
x
通过上述两题,总结
用二元一次方程组解
决实际问题的步骤
用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元法
总结提升
某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.
甲说:“我乘这种出租车走了11km,付了17元.”
乙说:“我乘这种出租车走了23km,付了35元.”
请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
分析 本问题涉及的等量关系有:
总车费=0~3km的车费(起步价)+超过3km的车费.
针对练习
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
解这个方程组,得
答:这种出租车的起步价是5元,超过3km后每千米收费1.5元.
起步价
超过3km后的费用
合计费用
甲
乙
x
x
(11-3)y
(23-3)y
17
35
今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?
牛五、羊二
牛二、羊五
5头牛、2只羊共价值10两“金”;2头牛、5只羊共价值8两“金”.问每头牛、每只羊各价值多少“金”?
解:设每头牛值“金”x两,每只羊值“金”y两,由题意,得
5x+2y=10,
2x+5y=8.
解得
x=
y=
{
答:羊值“金” 两,牛值“金” 两.
课堂练习
二元一次方程组的应用
步骤
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据两个等量关系列出方程组
解方程组
检验作答
课堂小结
第八章 二元一次方程组
能够根据具体的数量关系,列出二元一次方程组解决简单的实际问题.
学会利用二元一次方程组解决典型实际问题.
学习目标
问题1:解二元一次方程组主要有哪几种方法?
问题2:列一元一次方程解决实际问题的步骤有哪些?
审、设、列、解、验、答
代入消元法和加减消元法
温故知新
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李大叔估计的准确吗?
新课导入
问题1:题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2:题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为xkg和ykg,
探究新知
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组:x= ,
y= .
20
5
随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人,则:
+ = 42,
+ = 20.
8x
5y
4x
2y
解得:
x =4
y = 2
答:李大叔应聘请甲种饲养员4人,乙种饲养员2人.
例1:某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场,平几场?
分析:题中的未知量有胜的场数和平的场数,等量关系有:
胜的场数+平的场数=11;
胜场得分+平场得分=27.
胜场
平场
合计
场数
得分
x
3x
y
y
11
27
例题讲解
解:设市第二中学足球队胜x场,平y场.依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场,平3场.
x
通过上述两题,总结
用二元一次方程组解
决实际问题的步骤
用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元法
总结提升
某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.
甲说:“我乘这种出租车走了11km,付了17元.”
乙说:“我乘这种出租车走了23km,付了35元.”
请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
分析 本问题涉及的等量关系有:
总车费=0~3km的车费(起步价)+超过3km的车费.
针对练习
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
解这个方程组,得
答:这种出租车的起步价是5元,超过3km后每千米收费1.5元.
起步价
超过3km后的费用
合计费用
甲
乙
x
x
(11-3)y
(23-3)y
17
35
今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?
牛五、羊二
牛二、羊五
5头牛、2只羊共价值10两“金”;2头牛、5只羊共价值8两“金”.问每头牛、每只羊各价值多少“金”?
解:设每头牛值“金”x两,每只羊值“金”y两,由题意,得
5x+2y=10,
2x+5y=8.
解得
x=
y=
{
答:羊值“金” 两,牛值“金” 两.
课堂练习
二元一次方程组的应用
步骤
审题:弄清题意和题目中的数量关系
设元:用字母表示题目中的未知数
列方程组:根据两个等量关系列出方程组
解方程组
检验作答
课堂小结
