4.4 用尺规作三角形 一课一练(含解析)
文档属性
| 名称 | 4.4 用尺规作三角形 一课一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 16:19:42 | ||
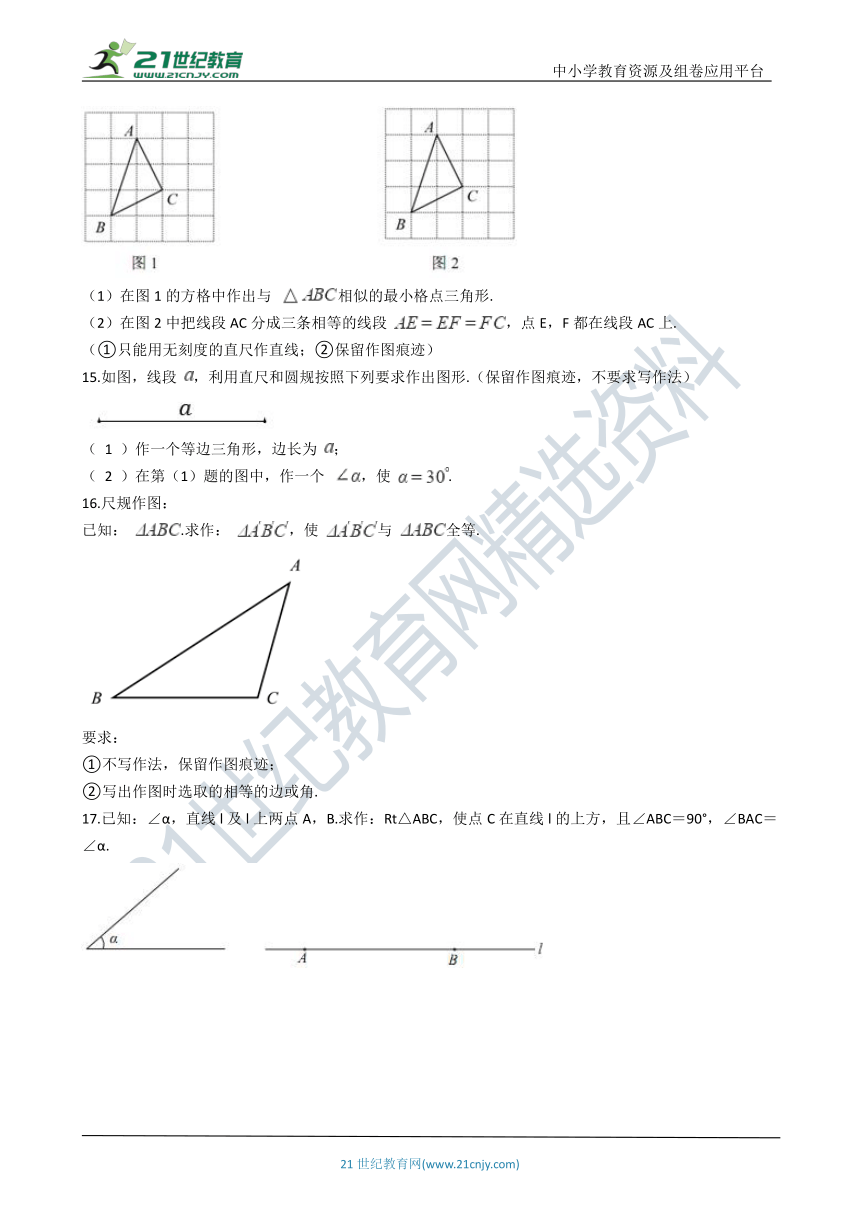
图片预览




文档简介
初中数学北师大版七年级下学期 第四章 4.4 用尺规作三角形
一、单选题
1.如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有(??? )
A.?6个???????????????????????????????????????B.?7个???????????????????????????????????????C.?8个???????????????????????????????????????D.?9个
2.如图,已知一条线段的长度为a,作边长为a的等边三角形的方法是:①画射线AM;②连结AC、BC;③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;④在射线AM上截取AB=a;以上画法正确的顺序是(? )
A.?①②③④???????????????????????????B.?①④③②???????????????????????????C.?①④②③???????????????????????????D.?②①④③
3.用尺规作图,下列条件中可能作出两个三角形的是(??? )
A.?已知两边和夹角???????????B.?已知两边及其一边的对角???????????C.?已知两角和夹边???????????D.?已知三条边
4.如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连接AB,AC,△ABC为所求的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是(?? )
A.?(1)??????????????????????????????????B.?(2)??????????????????????????????????C.?(3)??????????????????????????????????D.?(4)
5.如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为(?? )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
6.如图,在 中, ,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多为(? )
A.????????????????????????????????????????????B.????????????????????????????????????????????C.????????????????????????????????????????????D.?
二、填空题
7.???? 如下框内是“已知一条直角边和斜边作直角三角形”的尺规作图过程.
已知:线段a、b,
求作: 使得斜边 , .
作法:如图.
作射线AP,截取线段 ;
以AB为直径,作 ;
以点A为圆心,a的长为半径作弧交 于点C;
连接AC、CB.
即为所求作的直角三角形.
请您写出上述尺规作图的依据:________.
8.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出________个.
9.如图,∠EAD为锐角,C是射线AE上一点,点B在射线AD上运动(点A与点B不重合),设点C到AD的距离为d,BC长度为a,AC长度为b,在点B运动过程中,b、d保持不变,当a满足________条件时,△ABC唯一确定.
10.已知线段a,b,c,求作 ,使 , , ,下面作法的合理顺序为________(填序号)
①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;
②作直线 ,在 上截取 ;
③连接 , , 为所求作的三角形.
11.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出________个.
12.用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是________.
三、解答题
13.如图,已知 ,用直尺和圆规作 ,使得 .
14.在 的方格中, 的三个顶点都在格点上,我们把像这种顶点在格点的三角形叫格点三角形,请按要求完成下列作图
(1)在图1的方格中作出与 相似的最小格点三角形.
(2)在图2中把线段AC分成三条相等的线段 ,点E,F都在线段AC上.
(①只能用无刻度的直尺作直线;②保留作图痕迹)
15.如图,线段 ,利用直尺和圆规按照下列要求作出图形.(保留作图痕迹,不要求写作法)
( 1 )作一个等边三角形,边长为 ;
( 2 )在第(1)题的图中,作一个 ,使 .
16.尺规作图:
已知: .求作: ,使 与 全等.
要求:
①不写作法,保留作图痕迹;
②写出作图时选取的相等的边或角.
17.已知:∠α,直线l及l上两点A,B.求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
答案解析部分
一、单选题
1.【答案】 D
解:如图,以AB为底边有五个,以AB为腰则有四个.故共有9个,选D.
2.【答案】 B
解:已知一条线段的长度为a,作边长为a的等边三角形的方法是:
①画射线AM;
②在射线AM上截取AB=a;
③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;
④连结AC、BC.
△ABC即为所求作的三角形.
故答案为:B.
3.【答案】 B
解:A、C、D三个选项分别符合全等三角形的判定方法SAS,ASA,SSS,故能作出唯一三角形;
B、只有涉及的两个三角形同为锐角三角形或者钝角三角形时,才能成立。
故答案为:B
4.【答案】 C
解:(3)在直线MN上截取线段h,带有随意性,与作图语言的准确性不相符.
5.【答案】 C
解:如图,
①以B为圆心,BC长为半径画弧,交AB于点D,△BCD就是等腰三角形;
②以A为圆心,AC长为半径画弧,交AB于点E,△ACE就是等腰三角形;
③以C为圆心,BC长为半径画弧,交AC于点F,△BCF就是等腰三角形;
④作AC的垂直平分线交AB于点H,△ACH就是等腰三角形;
⑤作AB的垂直平分线交AC于G,则△AGB是等腰三角形;
⑥作BC的垂直平分线交AB于I,则△BCI是等腰三角形.
故答案为:C.
6.【答案】 D
解:如图:
故答案为: D .
二、填空题
7.【答案】 等圆的半径相等,直径所对的圆周角是直角,三角形定义 答案不唯一
解:根据作图得AB为直径,则利用圆周角定理可判断 ,从而得到 满足条件.
故答案为:等圆的半径相等,直径所对的圆周角是直角,三角形定义 答案不唯一 .
8.【答案】 6
解:如图:
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出三个三角形△ABG,△ABM,△ABH和原三角形全等.
所以可画出6个.
故答案为:6.
9.【答案】 a=d或a≥b
解:如图,过点C作CF⊥AB于点F,此时△ACF是直角三角形.①当点B与点F重合时,即 时,△ABC是直角三角形,△ABC唯一确定;
②当 时,如图,
半径为 的⊙C与射线AD有两个交点 、 ,
∴△ABC不是唯一的;②当 时,如图,
半径为 的⊙C与射线AD只有唯一交点 ,
∴△ABC唯一确定.
故答案是: 或 .
10.【答案】 ②①③
解:作三角形,使三角形的三边等于已知边,作图的顺序应该是:
②作直线BP,在BP上截取BC=a;
①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;
③连接AB,AC,△ABC为所求作的三角形.
所以合理的顺序为:②①③
11.【答案】 4
解:如图,能画4个.
能画4个,分别是以D为圆心,AB为半径画圆;以C为圆心,CA为半径画圆.两圆相交于两点(DE上下各一个),分别于D、E连接后,可得到两个三角形;以D为圆心,AC为半径画圆;以E为圆心,AB为半径画圆,两圆相交于两点(D、E上下各一个),分别于D、E连接后,可得到两个三角形,所以 这样的三角形最多可以画4个.
12.【答案】 a<b<a
解:如图所示,过点C作CD⊥AB,垂足为D,
∵∠B=30°,
∴CD= BC= a.
∵AC>CD,
∴ a<b,
∴ a<b<a.
故答案为: a<b<a.
三、解答题
13.【答案】 解:取M、N点,
14.【答案】 (1)解:∵ , ,
∴ ,
∴ 是等腰直角三角形,
如图,画出一个最小的等腰直角三角形;
(2)解:如图,
15.【答案】 解:如图,△ABC、 为所作;
16.【答案】 解:选取AB、BC、AC作图,使其分别等于A′B′、B′C′、A′C′,
如图,即为所作三角形:
17.【答案】 解:如图所示,Rt△ABC即为所求.
一、单选题
1.如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有(??? )
A.?6个???????????????????????????????????????B.?7个???????????????????????????????????????C.?8个???????????????????????????????????????D.?9个
2.如图,已知一条线段的长度为a,作边长为a的等边三角形的方法是:①画射线AM;②连结AC、BC;③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;④在射线AM上截取AB=a;以上画法正确的顺序是(? )
A.?①②③④???????????????????????????B.?①④③②???????????????????????????C.?①④②③???????????????????????????D.?②①④③
3.用尺规作图,下列条件中可能作出两个三角形的是(??? )
A.?已知两边和夹角???????????B.?已知两边及其一边的对角???????????C.?已知两角和夹边???????????D.?已知三条边
4.如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连接AB,AC,△ABC为所求的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是(?? )
A.?(1)??????????????????????????????????B.?(2)??????????????????????????????????C.?(3)??????????????????????????????????D.?(4)
5.如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为(?? )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
6.如图,在 中, ,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多为(? )
A.????????????????????????????????????????????B.????????????????????????????????????????????C.????????????????????????????????????????????D.?
二、填空题
7.???? 如下框内是“已知一条直角边和斜边作直角三角形”的尺规作图过程.
已知:线段a、b,
求作: 使得斜边 , .
作法:如图.
作射线AP,截取线段 ;
以AB为直径,作 ;
以点A为圆心,a的长为半径作弧交 于点C;
连接AC、CB.
即为所求作的直角三角形.
请您写出上述尺规作图的依据:________.
8.如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出________个.
9.如图,∠EAD为锐角,C是射线AE上一点,点B在射线AD上运动(点A与点B不重合),设点C到AD的距离为d,BC长度为a,AC长度为b,在点B运动过程中,b、d保持不变,当a满足________条件时,△ABC唯一确定.
10.已知线段a,b,c,求作 ,使 , , ,下面作法的合理顺序为________(填序号)
①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;
②作直线 ,在 上截取 ;
③连接 , , 为所求作的三角形.
11.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出________个.
12.用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是________.
三、解答题
13.如图,已知 ,用直尺和圆规作 ,使得 .
14.在 的方格中, 的三个顶点都在格点上,我们把像这种顶点在格点的三角形叫格点三角形,请按要求完成下列作图
(1)在图1的方格中作出与 相似的最小格点三角形.
(2)在图2中把线段AC分成三条相等的线段 ,点E,F都在线段AC上.
(①只能用无刻度的直尺作直线;②保留作图痕迹)
15.如图,线段 ,利用直尺和圆规按照下列要求作出图形.(保留作图痕迹,不要求写作法)
( 1 )作一个等边三角形,边长为 ;
( 2 )在第(1)题的图中,作一个 ,使 .
16.尺规作图:
已知: .求作: ,使 与 全等.
要求:
①不写作法,保留作图痕迹;
②写出作图时选取的相等的边或角.
17.已知:∠α,直线l及l上两点A,B.求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
答案解析部分
一、单选题
1.【答案】 D
解:如图,以AB为底边有五个,以AB为腰则有四个.故共有9个,选D.
2.【答案】 B
解:已知一条线段的长度为a,作边长为a的等边三角形的方法是:
①画射线AM;
②在射线AM上截取AB=a;
③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;
④连结AC、BC.
△ABC即为所求作的三角形.
故答案为:B.
3.【答案】 B
解:A、C、D三个选项分别符合全等三角形的判定方法SAS,ASA,SSS,故能作出唯一三角形;
B、只有涉及的两个三角形同为锐角三角形或者钝角三角形时,才能成立。
故答案为:B
4.【答案】 C
解:(3)在直线MN上截取线段h,带有随意性,与作图语言的准确性不相符.
5.【答案】 C
解:如图,
①以B为圆心,BC长为半径画弧,交AB于点D,△BCD就是等腰三角形;
②以A为圆心,AC长为半径画弧,交AB于点E,△ACE就是等腰三角形;
③以C为圆心,BC长为半径画弧,交AC于点F,△BCF就是等腰三角形;
④作AC的垂直平分线交AB于点H,△ACH就是等腰三角形;
⑤作AB的垂直平分线交AC于G,则△AGB是等腰三角形;
⑥作BC的垂直平分线交AB于I,则△BCI是等腰三角形.
故答案为:C.
6.【答案】 D
解:如图:
故答案为: D .
二、填空题
7.【答案】 等圆的半径相等,直径所对的圆周角是直角,三角形定义 答案不唯一
解:根据作图得AB为直径,则利用圆周角定理可判断 ,从而得到 满足条件.
故答案为:等圆的半径相等,直径所对的圆周角是直角,三角形定义 答案不唯一 .
8.【答案】 6
解:如图:
以BC为公共边可画出△BDC,△BEC,△BFC三个三角形和原三角形全等.
以AB为公共边可画出三个三角形△ABG,△ABM,△ABH和原三角形全等.
所以可画出6个.
故答案为:6.
9.【答案】 a=d或a≥b
解:如图,过点C作CF⊥AB于点F,此时△ACF是直角三角形.①当点B与点F重合时,即 时,△ABC是直角三角形,△ABC唯一确定;
②当 时,如图,
半径为 的⊙C与射线AD有两个交点 、 ,
∴△ABC不是唯一的;②当 时,如图,
半径为 的⊙C与射线AD只有唯一交点 ,
∴△ABC唯一确定.
故答案是: 或 .
10.【答案】 ②①③
解:作三角形,使三角形的三边等于已知边,作图的顺序应该是:
②作直线BP,在BP上截取BC=a;
①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;
③连接AB,AC,△ABC为所求作的三角形.
所以合理的顺序为:②①③
11.【答案】 4
解:如图,能画4个.
能画4个,分别是以D为圆心,AB为半径画圆;以C为圆心,CA为半径画圆.两圆相交于两点(DE上下各一个),分别于D、E连接后,可得到两个三角形;以D为圆心,AC为半径画圆;以E为圆心,AB为半径画圆,两圆相交于两点(D、E上下各一个),分别于D、E连接后,可得到两个三角形,所以 这样的三角形最多可以画4个.
12.【答案】 a<b<a
解:如图所示,过点C作CD⊥AB,垂足为D,
∵∠B=30°,
∴CD= BC= a.
∵AC>CD,
∴ a<b,
∴ a<b<a.
故答案为: a<b<a.
三、解答题
13.【答案】 解:取M、N点,
14.【答案】 (1)解:∵ , ,
∴ ,
∴ 是等腰直角三角形,
如图,画出一个最小的等腰直角三角形;
(2)解:如图,
15.【答案】 解:如图,△ABC、 为所作;
16.【答案】 解:选取AB、BC、AC作图,使其分别等于A′B′、B′C′、A′C′,
如图,即为所作三角形:
17.【答案】 解:如图所示,Rt△ABC即为所求.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
