4.5 利用三角形全等测距离 一课一练(含解析)
文档属性
| 名称 | 4.5 利用三角形全等测距离 一课一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 13:45:18 | ||
图片预览



文档简介
初中数学北师大版七年级下学期 第四章 4.5 利用三角形全等测距离
一、单选题
1.要测量河两岸相对的两点 , 的距离,先在 的垂线 上取两点 , ,使 ,再作出 的垂线 ,使 , , 在一条直线上(如图),可以说明 ,得 ,因此测得 的长就是 的长.判定 最恰当的理由是(?? )
A.?边角边?????????????????????????????B.?角边角?????????????????????????????C.?边边边?????????????????????????????D.?斜边、直角边
2.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是(?? )
A.?a???????????????????????????????????B.?b???????????????????????????????????C.?b﹣a???????????????????????????????????D.?(b﹣a)
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( ?)
A.?带①去?????????????????????????????B.?带②去?????????????????????????????C.?带③去?????????????????????????????D.?①②③都带去
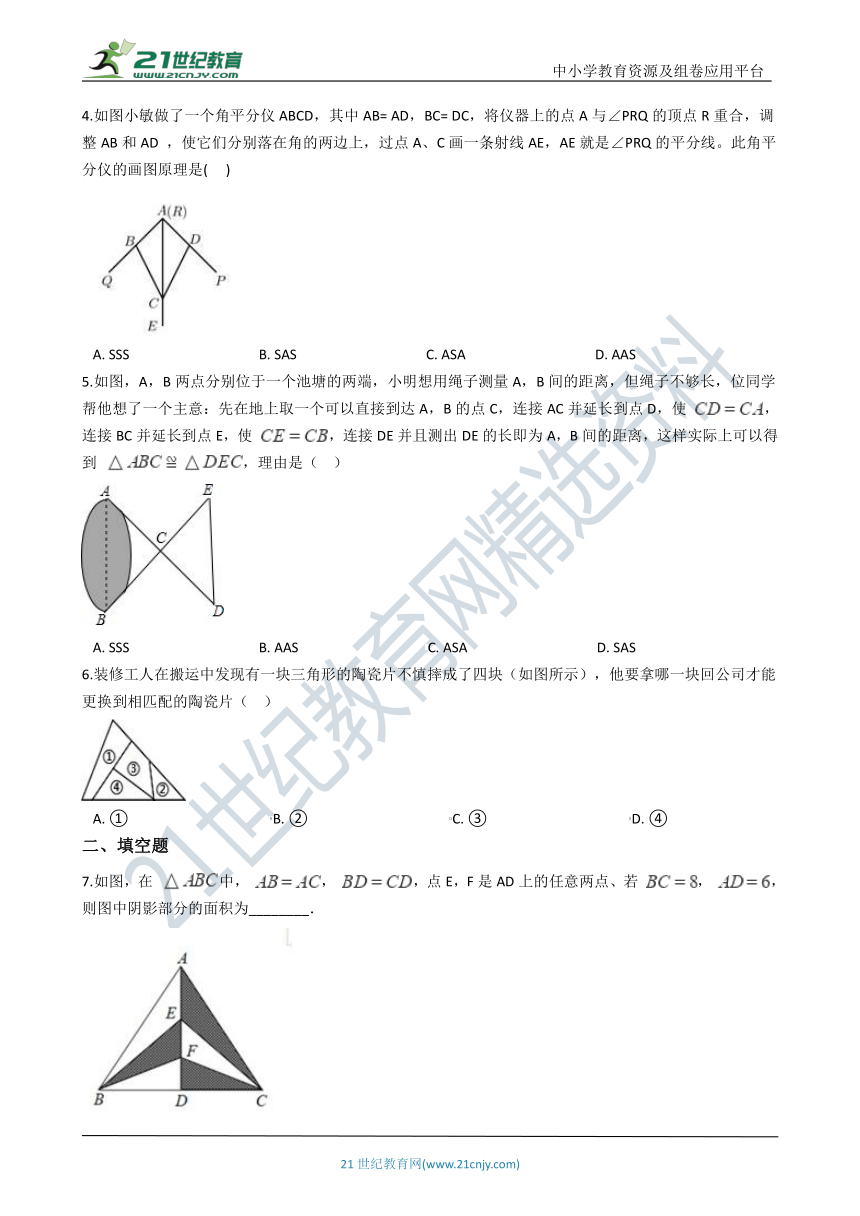
4.如图小敏做了一个角平分仪ABCD,其中AB= AD,BC= DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD ,使它们分别落在角的两边上,过点A、C画一条射线AE,AE就是∠PRQ的平分线。此角平分仪的画图原理是(?? ?)
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?AAS
5.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使 ,连接BC并延长到点E,使 ,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到 ,理由是(?? )
A.?SSS?????????????????????????????????????B.?AAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?SAS
6.装修工人在搬运中发现有一块三角形的陶瓷片不慎摔成了四块(如图所示),他要拿哪一块回公司才能更换到相匹配的陶瓷片(?? )
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
二、填空题
7.如图,在 中, , ,点E,F是AD上的任意两点、若 , ,则图中阴影部分的面积为________.
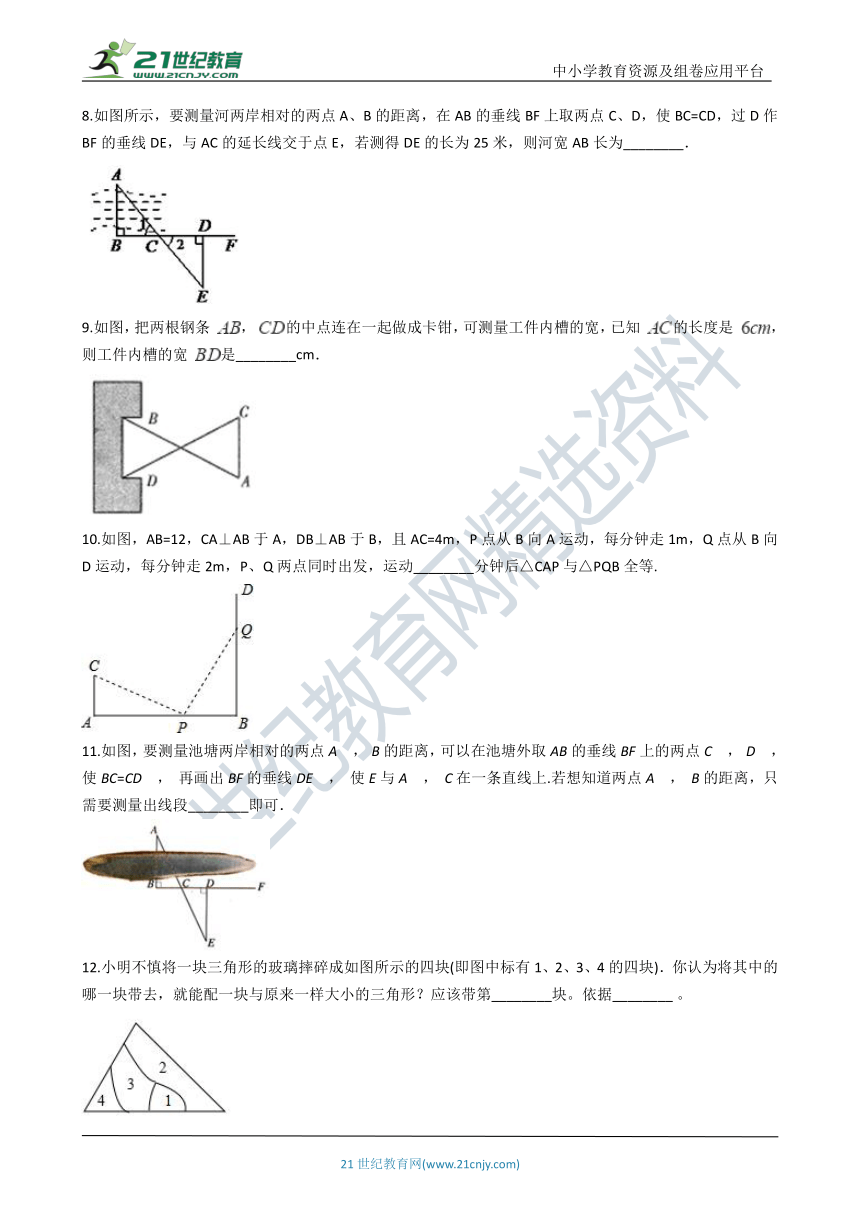
8.如图所示,要测量河两岸相对的两点A、B的距离,在AB的垂线BF上取两点C、D,使BC=CD,过D作BF的垂线DE,与AC的延长线交于点E,若测得DE的长为25米,则河宽AB长为________.
9.如图,把两根钢条 , 的中点连在一起做成卡钳,可测量工件内槽的宽,已知 的长度是 ,则工件内槽的宽 是________cm.
10.如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动________分钟后△CAP与△PQB全等.
11.如图,要测量池塘两岸相对的两点A , B的距离,可以在池塘外取AB的垂线BF上的两点C , D , 使BC=CD , 再画出BF的垂线DE , 使E与A , C在一条直线上.若想知道两点A , B的距离,只需要测量出线段________即可.
12.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块).你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第________块。依据________?。
三、解答题
13.如图,工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器,只有一个刻度尺.他是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长为a m,FG的长为b m.如果a=b,则说明∠B和∠C是相等的,他的这种做法合理吗?为什么?
14.如图所示,C、D分别位于路段A、B两点的正北处与正南处,现有两车分别从E、F两处出发,以相同的速度直线行驶,相同时间后分别到达C、D两地,休整一段时间后又以原来的速度直线行驶,最终同时到达A、B两点,那么CE与DF平行吗?为什么?
15.某中学八年级同学到野外开展数学综合实践活动,在营地看到一池塘,同学们想知道池塘两端的距离.某同学设计了如下测量方案:先取一个可直接到达池塘的两端的点 , 的点 ,连接 , ,分别延长 至点 , 至点 ,使得 , .再测出 的长度即可知道 之间的距离.他的方案可行吗?请说明理由.
16.如图,一根电线杆 直立在水平地面上的点 处,分别用钢丝绳 , 将它加固,两根钢丝绳分别固定在地面上的点 处,点 在同一条直线上,小明测得 ,两根钢丝绳相等吗?请说明理由.
17.仅用一块没有刻度的直角三角板能画出图1∠AOB的平分线吗?
小刚想出了这样的方法:如图2所示,先将直角三角板的一个锐角顶点和∠AOB的顶点O重合,一条直角边与OA重叠(重叠部分为OC),沿另一条直角边画出直线m;再将三角板的同一锐角顶点与O重合,同一条直角边与OB重叠(重叠部分为OD),沿另一条直角边画山直线n,m与n交于点P,连接OP并延长,则射线OP为∠AOB的平分线,你认为小刚的方法正确吗?为什么?
18.你一定玩过跷跷板吧!如图是小明和小刚玩跷跷板的示意图,横板绕它的中点O上下转动,立柱OC与地面垂直.当一方着地时,另一方上升到最高点.问:在上下转动横板的过程中,两人上升的最大高度AA′、BB′有何数量关系,为什么?
答案解析部分
一、单选题
1.【答案】 B
解:在△ABC和△EDC中,
∵∠ACB=∠ECD,BC=CD,
又∵AB⊥BF,DE⊥BF,
∴∠ABC=∠EDC=90゜,
∴△ABC≌△EDC(ASA),
∴AB=ED.
故答案为:B.
2.【答案】 D
解:在 和 中,
?
∴ ≌ ,
∴
∵EF=b
∴圆形容器的壁厚是
故答案为:D.
3.【答案】 C
解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故答案为:C.
4.【答案】 A
解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠CAD.
故答案为:A.
5.【答案】 D
解:在 与 中,
∴AB=DE.
故答案为:D.
6.【答案】 A
解: ①?包括大三角形的两个角以及这两个角的夹边,根据ASA定理可知拿①去配,可以更换到相匹配的陶瓷片.
故答案为:A.
二、填空题
7.【答案】 12
解:∵AB=AC,BD=CD,AD=AD,
∴△ADC≌△ADB(SSS),
∴S△ADC=S△ADB ,
∵BC=8,
∴BD=4,
∵AB=AC,BD=DC,
∴AD⊥BC,
∴EB=EC,FB=FC,
∵EF=EF,
∴△BEF≌△CEF(SSS)
∴S△BEF=S△CEF ,
∵AD=6,
∴S阴影=S△ADB= BD?AD= ×4×6=12.
故答案为:12.
8.【答案】 25米
解:根据题意可知∠B=∠D=90°,BC=CD,∠ACB=∠ECD,
∴△ABC≌△EDC,
∴AB=DE=25米.
故答案为:25米
9.【答案】 6
解:如图,设点O是 , 的中点,
∴OB=OA,OC=OD,
在△BOD和△AOC中,
∵OB=OA,∠BOD=∠AOC,OD=OC,
∴△BOD≌△AOC(SAS),
∴BD=AC=6cm.
故答案为:6.
10.【答案】 4
解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12-x)m,
分两种情况:
①若BP=AC,则x=4,
AP=12-4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12-x=x,
解得:x=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故答案为:4.
11.【答案】 DE
解:根据题意可知∠B=∠D=90°,BC=CD,∠ACB=∠ECD
∴△ABC≌△EDC
∴AB=DE
即只需要测量出线段DE即可.
故答案为:DE
12.【答案】 2;ASA
解:∵第二块有完整的两角和夹边,可以利用角边角定理找到和和原来三角形全等的三角形,符合题意,其他几块都没有三角形全等完整的的三要素.
故答案为:2,ASA.
三、解答题
13.【答案】 证明:这种做法合理,理由如下:在△BDE和△CFG中,BE=CG;BD=CF;DE=FG∴△BDE≌△CFG(SSS),∴∠B=∠C。故这种做法合理,
14.【答案】 解: .
证明:∵C、D分别位于路段A、B两点的正北处与正南处,
∴∠A=∠B=90°,
∵两车分别从E、F两处出发,以相同的速度直线行驶,相同时间后分别到达C、D两地,
∴CE=DF,
∵两车以原来的速度从C、D两地直线行驶,最终同时到达A,B两点,
∴AC=BD,
∵
∴ (HL).
∴ .
∴ .
15.【答案】 解:可行.理由如下:
在 和 中,
.
16.【答案】 解:相等,理由如下:
∵BN=CN,
由题意得:AN⊥BC,
∴∠ANC=∠ANB,
∵AN=AN,
∴△ABN≌△ACN(SAS),
∴AB=AC.
17.【答案】 解:正确,理由如下:
∵OC和OD是三角板的同一条直角边,
∴OC=OD,
∵OP=OP,
∴Rt△ODP≌Rt△OCP(HL),
∴∠POD=∠POC.
即射线OP为∠AOB的平分线.
18.【答案】解:数量关系:AA′=BB′;
理由如下:
∵O是AB′、A′B的中点,
∴OA=OB′,OA′=OB,
在△A′OA与△BOB′中,
,
∴△A′OA≌△BOB′(SAS),
∴AA′=BB′.
一、单选题
1.要测量河两岸相对的两点 , 的距离,先在 的垂线 上取两点 , ,使 ,再作出 的垂线 ,使 , , 在一条直线上(如图),可以说明 ,得 ,因此测得 的长就是 的长.判定 最恰当的理由是(?? )
A.?边角边?????????????????????????????B.?角边角?????????????????????????????C.?边边边?????????????????????????????D.?斜边、直角边
2.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是(?? )
A.?a???????????????????????????????????B.?b???????????????????????????????????C.?b﹣a???????????????????????????????????D.?(b﹣a)
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( ?)
A.?带①去?????????????????????????????B.?带②去?????????????????????????????C.?带③去?????????????????????????????D.?①②③都带去
4.如图小敏做了一个角平分仪ABCD,其中AB= AD,BC= DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD ,使它们分别落在角的两边上,过点A、C画一条射线AE,AE就是∠PRQ的平分线。此角平分仪的画图原理是(?? ?)
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?AAS
5.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使 ,连接BC并延长到点E,使 ,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到 ,理由是(?? )
A.?SSS?????????????????????????????????????B.?AAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?SAS
6.装修工人在搬运中发现有一块三角形的陶瓷片不慎摔成了四块(如图所示),他要拿哪一块回公司才能更换到相匹配的陶瓷片(?? )
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
二、填空题
7.如图,在 中, , ,点E,F是AD上的任意两点、若 , ,则图中阴影部分的面积为________.
8.如图所示,要测量河两岸相对的两点A、B的距离,在AB的垂线BF上取两点C、D,使BC=CD,过D作BF的垂线DE,与AC的延长线交于点E,若测得DE的长为25米,则河宽AB长为________.
9.如图,把两根钢条 , 的中点连在一起做成卡钳,可测量工件内槽的宽,已知 的长度是 ,则工件内槽的宽 是________cm.
10.如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动________分钟后△CAP与△PQB全等.
11.如图,要测量池塘两岸相对的两点A , B的距离,可以在池塘外取AB的垂线BF上的两点C , D , 使BC=CD , 再画出BF的垂线DE , 使E与A , C在一条直线上.若想知道两点A , B的距离,只需要测量出线段________即可.
12.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块).你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第________块。依据________?。
三、解答题
13.如图,工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器,只有一个刻度尺.他是这样操作的:①分别在BA和CA上取BE=CG;②在BC上取BD=CF;③量出DE的长为a m,FG的长为b m.如果a=b,则说明∠B和∠C是相等的,他的这种做法合理吗?为什么?
14.如图所示,C、D分别位于路段A、B两点的正北处与正南处,现有两车分别从E、F两处出发,以相同的速度直线行驶,相同时间后分别到达C、D两地,休整一段时间后又以原来的速度直线行驶,最终同时到达A、B两点,那么CE与DF平行吗?为什么?
15.某中学八年级同学到野外开展数学综合实践活动,在营地看到一池塘,同学们想知道池塘两端的距离.某同学设计了如下测量方案:先取一个可直接到达池塘的两端的点 , 的点 ,连接 , ,分别延长 至点 , 至点 ,使得 , .再测出 的长度即可知道 之间的距离.他的方案可行吗?请说明理由.
16.如图,一根电线杆 直立在水平地面上的点 处,分别用钢丝绳 , 将它加固,两根钢丝绳分别固定在地面上的点 处,点 在同一条直线上,小明测得 ,两根钢丝绳相等吗?请说明理由.
17.仅用一块没有刻度的直角三角板能画出图1∠AOB的平分线吗?
小刚想出了这样的方法:如图2所示,先将直角三角板的一个锐角顶点和∠AOB的顶点O重合,一条直角边与OA重叠(重叠部分为OC),沿另一条直角边画出直线m;再将三角板的同一锐角顶点与O重合,同一条直角边与OB重叠(重叠部分为OD),沿另一条直角边画山直线n,m与n交于点P,连接OP并延长,则射线OP为∠AOB的平分线,你认为小刚的方法正确吗?为什么?
18.你一定玩过跷跷板吧!如图是小明和小刚玩跷跷板的示意图,横板绕它的中点O上下转动,立柱OC与地面垂直.当一方着地时,另一方上升到最高点.问:在上下转动横板的过程中,两人上升的最大高度AA′、BB′有何数量关系,为什么?
答案解析部分
一、单选题
1.【答案】 B
解:在△ABC和△EDC中,
∵∠ACB=∠ECD,BC=CD,
又∵AB⊥BF,DE⊥BF,
∴∠ABC=∠EDC=90゜,
∴△ABC≌△EDC(ASA),
∴AB=ED.
故答案为:B.
2.【答案】 D
解:在 和 中,
?
∴ ≌ ,
∴
∵EF=b
∴圆形容器的壁厚是
故答案为:D.
3.【答案】 C
解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故答案为:C.
4.【答案】 A
解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠CAD.
故答案为:A.
5.【答案】 D
解:在 与 中,
∴AB=DE.
故答案为:D.
6.【答案】 A
解: ①?包括大三角形的两个角以及这两个角的夹边,根据ASA定理可知拿①去配,可以更换到相匹配的陶瓷片.
故答案为:A.
二、填空题
7.【答案】 12
解:∵AB=AC,BD=CD,AD=AD,
∴△ADC≌△ADB(SSS),
∴S△ADC=S△ADB ,
∵BC=8,
∴BD=4,
∵AB=AC,BD=DC,
∴AD⊥BC,
∴EB=EC,FB=FC,
∵EF=EF,
∴△BEF≌△CEF(SSS)
∴S△BEF=S△CEF ,
∵AD=6,
∴S阴影=S△ADB= BD?AD= ×4×6=12.
故答案为:12.
8.【答案】 25米
解:根据题意可知∠B=∠D=90°,BC=CD,∠ACB=∠ECD,
∴△ABC≌△EDC,
∴AB=DE=25米.
故答案为:25米
9.【答案】 6
解:如图,设点O是 , 的中点,
∴OB=OA,OC=OD,
在△BOD和△AOC中,
∵OB=OA,∠BOD=∠AOC,OD=OC,
∴△BOD≌△AOC(SAS),
∴BD=AC=6cm.
故答案为:6.
10.【答案】 4
解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12-x)m,
分两种情况:
①若BP=AC,则x=4,
AP=12-4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12-x=x,
解得:x=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故答案为:4.
11.【答案】 DE
解:根据题意可知∠B=∠D=90°,BC=CD,∠ACB=∠ECD
∴△ABC≌△EDC
∴AB=DE
即只需要测量出线段DE即可.
故答案为:DE
12.【答案】 2;ASA
解:∵第二块有完整的两角和夹边,可以利用角边角定理找到和和原来三角形全等的三角形,符合题意,其他几块都没有三角形全等完整的的三要素.
故答案为:2,ASA.
三、解答题
13.【答案】 证明:这种做法合理,理由如下:在△BDE和△CFG中,BE=CG;BD=CF;DE=FG∴△BDE≌△CFG(SSS),∴∠B=∠C。故这种做法合理,
14.【答案】 解: .
证明:∵C、D分别位于路段A、B两点的正北处与正南处,
∴∠A=∠B=90°,
∵两车分别从E、F两处出发,以相同的速度直线行驶,相同时间后分别到达C、D两地,
∴CE=DF,
∵两车以原来的速度从C、D两地直线行驶,最终同时到达A,B两点,
∴AC=BD,
∵
∴ (HL).
∴ .
∴ .
15.【答案】 解:可行.理由如下:
在 和 中,
.
16.【答案】 解:相等,理由如下:
∵BN=CN,
由题意得:AN⊥BC,
∴∠ANC=∠ANB,
∵AN=AN,
∴△ABN≌△ACN(SAS),
∴AB=AC.
17.【答案】 解:正确,理由如下:
∵OC和OD是三角板的同一条直角边,
∴OC=OD,
∵OP=OP,
∴Rt△ODP≌Rt△OCP(HL),
∴∠POD=∠POC.
即射线OP为∠AOB的平分线.
18.【答案】解:数量关系:AA′=BB′;
理由如下:
∵O是AB′、A′B的中点,
∴OA=OB′,OA′=OB,
在△A′OA与△BOB′中,
,
∴△A′OA≌△BOB′(SAS),
∴AA′=BB′.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
