第四章 三角形单元测试题（含解析）

初中数学北师大版七年级下学期 第四章 单元测试卷
一、单选题（共8题；每题3分；共24分）
1.在下列长度的四根木棒中，能与2m、5m长的两根木棒钉成一个三角形的是（?? ）
A.?2m???????????????????????????????????????B.?3m???????????????????????????????????????C.?5m???????????????????????????????????????D.?7m
2.等腰三角形两边长为3和6，则周长为（?? ）
A.?12???????????????????????????????????B.?15???????????????????????????????????C.?12或15???????????????????????????????????D.?无法确定
3.如图，若△ABC≌△DEF，BE＝22，BF＝5，则FC的长度是（? ）
A.?10?????????????????????????????????????????B.?12?????????????????????????????????????????C.?8?????????????????????????????????????????D.?16
4.如图所示是两个全等三角形，由图中条件可知，

A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?或
5.如图，△ABC≌△CDA，∠BAC＝∠DCA，则BC 的对应边是 （?? ）
A.?CD???????????????????????????????????????B.?CA???????????????????????????????????????C.?DA???????????????????????????????????????D.?AB
6.如图，在 中， 于 ， 于 ， 与 交于点 ．请你添加一个适当的条件，使 ≌ ．下列添加的条件错误的是（? ）
A.????????????????????????B.????????????????????????C.????????????????????????D.?
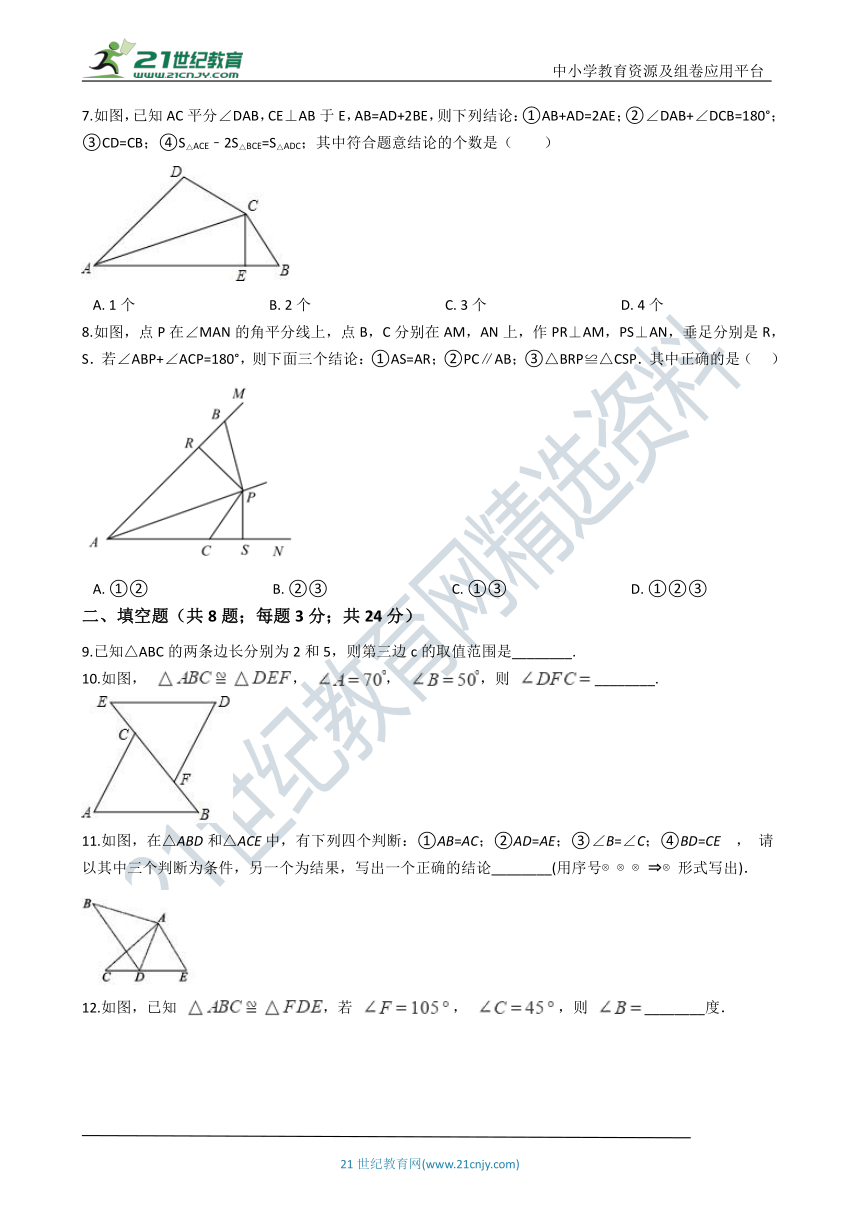
7.如图，已知AC平分∠DAB，CE⊥AB于E，AB=AD+2BE，则下列结论：①AB+AD=2AE；②∠DAB+∠DCB=180°；③CD=CB；④S△ACE﹣2S△BCE=S△ADC；其中符合题意结论的个数是（　　）??
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
8.如图，点P在∠MAN的角平分线上，点B，C分别在AM，AN上，作PR⊥AM，PS⊥AN，垂足分别是R，S．若∠ABP+∠ACP=180°，则下面三个结论：①AS=AR；②PC∥AB；③△BRP≌△CSP．其中正确的是（??? ）
A.?①②????????????????????????????????????B.?②③????????????????????????????????????C.?①③????????????????????????????????????D.?①②③
二、填空题（共8题；每题3分；共24分）
9.已知△ABC的两条边长分别为2和5，则第三边c的取值范围是________.
10.如图， ， ， ，则 ________.
11.如图，在△ABD和△ACE中，有下列四个判断：①AB=AC；②AD=AE；③∠B=∠C；④BD=CE ， 请以其中三个判断为条件，另一个为结果，写出一个正确的结论________(用序号?????形式写出)．
12.如图，已知 ，若 ， ，则 ________度．
13.如图，在△ABC中，AB＝BC，BE平分∠ABC，AD为BC边上的高，且AD＝BD．则∠3＝________°．
14.如图，在 中， ， 为 边 上一点， ， 平分 的外角，且 .连接 交 于 为边 上一点，满足 ，连接 交 于H.以下结论：① ；② ；③ ；④若 平分 ，则 平分 正确的是________.
15.如图，在△ABC中，AB＝AC＝24厘米，∠B=∠C ,BC＝16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为________厘米/秒时，能够在某一时刻使△BPD与△CQP全等．
16.如图，∠A＝∠B＝90°，AB＝60，E，F 分别为线段 AB 和射线 BD 上的一点，若点 E 从点 B 出发向点 A 运动，同时点 F 从点 B 出发向点 D 运动，二者速度之比为 3：7，运动到某时刻同时停止，在射线 AC 上取一点 G，使△AEG 与△BEF 全等，则 AG 的长为________.
三、解答题（共10题；共72分）
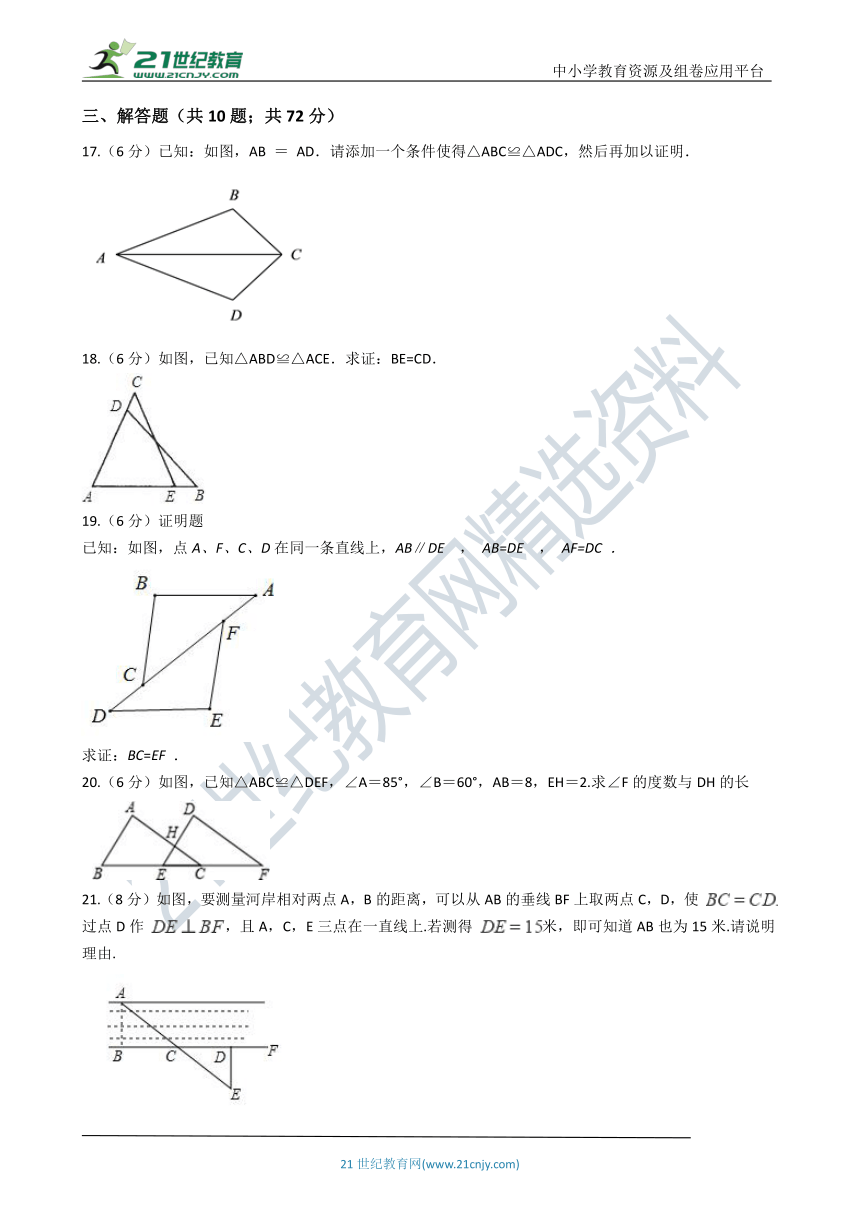
17.（6分）已知：如图，AB ＝ AD．请添加一个条件使得△ABC≌△ADC，然后再加以证明．
18.（6分）如图，已知△ABD≌△ACE．求证：BE=CD．
19.（6分）证明题
已知：如图，点A、F、C、D在同一条直线上，AB∥DE ， AB=DE ， AF=DC ．
求证：BC=EF ．
20.（6分）如图，已知△ABC≌△DEF，∠A＝85°，∠B＝60°，AB＝8，EH＝2.求∠F的度数与DH的长
?
21.（8分）如图，要测量河岸相对两点A，B的距离，可以从AB的垂线BF上取两点C，D，使 过点D作 ，且A，C，E三点在一直线上.若测得 米，即可知道AB也为15米.请说明理由.

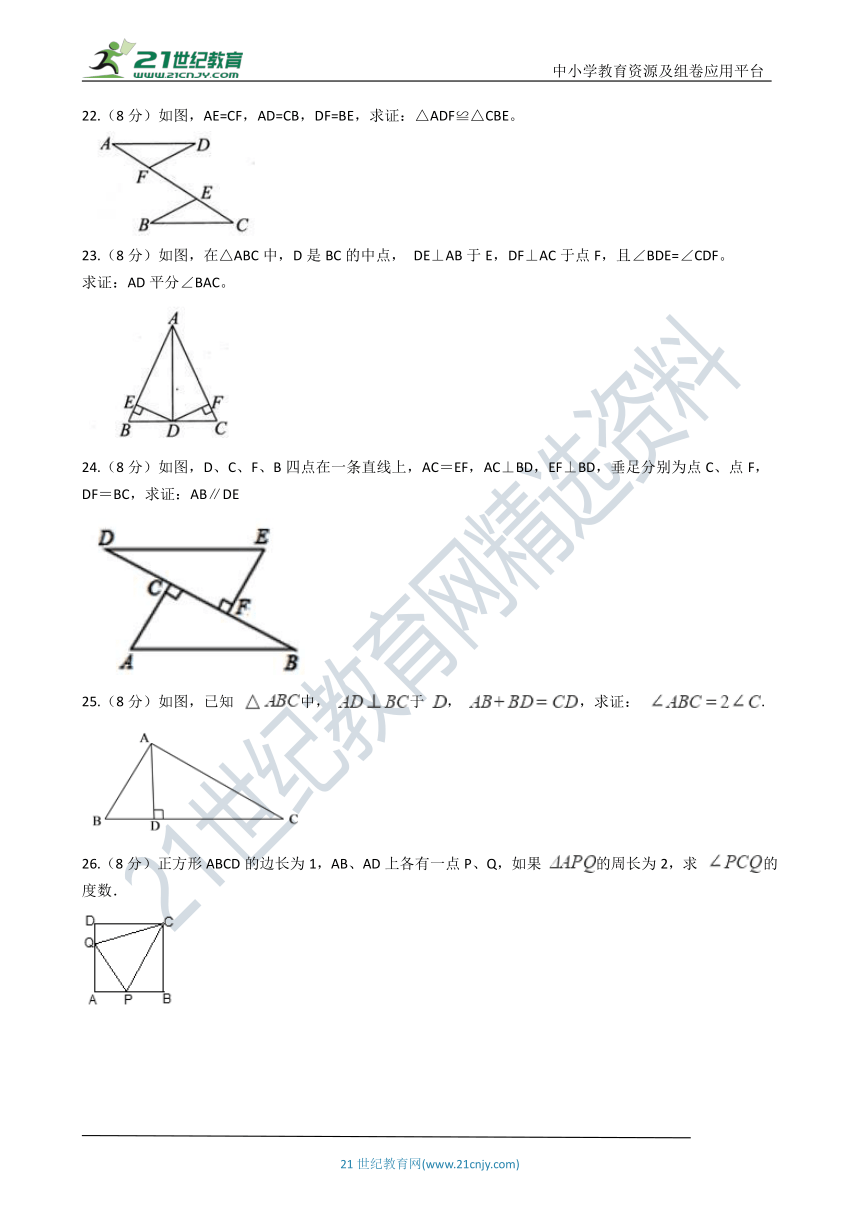
22.（8分）如图，AE=CF，AD=CB，DF=BE，求证：△ADF≌△CBE。

23.（8分）如图，在△ABC中，D是BC的中点， DE⊥AB于E，DF⊥AC于点F，且∠BDE=∠CDF。
求证：AD平分∠BAC。

24.（8分）如图，D、C、F、B四点在一条直线上，AC＝EF，AC⊥BD，EF⊥BD，垂足分别为点C、点F，DF＝BC，求证：AB∥DE
25.（8分）如图，已知 中， 于 ， ，求证： .
26.（8分）正方形ABCD的边长为1，AB、AD上各有一点P、Q，如果 的周长为2，求 的度数．
答案解析部分
一、单选题
1.【答案】 C
解：设三角形的第三边为x m，则
5-2＜x＜5+2
即3＜x＜7，
∴当x=5时，能与2m、5m长的两根木棒钉成一个三角形.
故答案为：C.
2.【答案】 B
解：∵三角形中任意两边之和大于第三边
∴当另一边为3时3+3=6不符，
∴另一边必须为6，
∴周长为3+6+6=15.
故答案为：B.
3.【答案】 B
解：∵BE＝22，BF＝5，
∴EF=BE-BF=17，
∵△ABC≌△DEF，
∴BC=EF=17，
∴FC=BC-BF=12．
故答案为：B
4.【答案】 A
解：如图， ，
两个三角形全等，
.
故答案为：A.
5.【答案】 C
解：∵ △ABC≌△CDA，∠BAC＝∠DCA，
∴BC=DA
∴BC的对应边是DA.
故答案为：C.
6.【答案】 D
解：∵AD⊥BC，CE⊥AB，垂足分别为D、E，
∴∠AEF=∠CEB=90°，∠ADB=∠ADC=90°，
∴∠EAF+∠B=90°，∠BCE+∠B=90°，
∴∠EAF=∠BCE．
A.在Rt△AEF和Rt△CEB中
∴ ≌ （AAS），故不符合题意；
B.在Rt△AEF和Rt△CEB中
∴ ≌ （ASA），故不符合题意；
C.在Rt△AEF和Rt△CEB中
∴ ≌ （AAS），故不符合题意；
D.在Rt△AEF和Rt△CEB中
由 不能证明 ≌ ，故符合题意；
故答案为：D．
7.【答案】 C
解：①在AE取点F，使EF=BE，
∵AB=AD+2BE=AF+EF+BE，EF=BE，
∴AB=AD+2BE=AF+2BE，
∴AD=AF，
∴AB+AD=AF+EF+BE+AD=2AF+2EF=2（AF+EF）=2AE，
∴AE= （AB+AD），故①符合题意；
②在AB上取点F，使BE=EF，连接CF．
在△ACD与△ACF中，∵AD=AF，∠DAC=∠FAC，AC=AC，
∴△ACD≌△ACF，
∴∠ADC=∠AFC．
∵CE垂直平分BF，
∴CF=CB，
∴∠CFB=∠B．
又∵∠AFC+∠CFB=180°，
∴∠ADC+∠B=180°，
∴∠DAB+∠DCB=360-（∠ADC+∠B）=180°，故②符合题意；
③由②知，△ACD≌△ACF，∴CD=CF，
又∵CF=CB，
∴CD=CB，故③符合题意；
④易证△CEF≌△CEB，
所以S△ACE-S△BCE=S△ACE-S△FCE=S△ACF ，
又∵△ACD≌△ACF，
∴S△ACF=S△ADC ，
∴S△ACE-S△BCE=S△ADC ， 故④不符合题意；
即正确的有3个，
故答案为：C．
8.【答案】 C
解：∵点 P 在∠MAN的角平分上，PR⊥AM， PS⊥AN，
∴PR=PS，
∵∠ARP=∠ASP=90°，
∴在Rt△APR和Rt△APS中，
，
∴△APR≌△APS（HL），
∴AS=AR，故①符合题意；
∵∠ABP +∠ACP = 180°，
∴∠ABP=∠PCS，
又∵PR=PS，∠PRB=∠PSC=90°，
∴△BRP≌△CSP（AAS），故③符合题意；
若∠MAP=∠CPA，则PC∥AB，
则需要AC=PC得出∠PAN=∠CPA，
从而根据∠MAP=∠PAN，
得出∠MAP=∠CPA，
而题中没有条件说明AC=PC，故②不符合题意；
故答案为：C．
二、填空题
9.【答案】 3＜c＜7
解：由题意，得
5﹣2＜c＜5+2，
即3＜c＜7.
故答案为：3＜c＜7.
10.【答案】 60°
解：∵△ABC≌△DEF，
∴∠A=∠D=70°，∠B=∠E=50°，
∴∠DFC=180°-(∠D+∠E)=180°-120°=60°，
故答案为：60°.
11.【答案】 ①②④?③或①③④?②
解：由①②④?③或①③④?②；
先证前一种：
∵AB=AC ， AD=AE ， BD=CE ，
∴△ABD≌△ACE(SSS)；
∴∠B=∠C；
再证第二种：
∵AB=AC ， ∠B=∠C ， BD=CE ，
∴△ABD≌△ACE(SAS)；
∴AD=AE.
故答案为①②④?③或①③④?②；
12.【答案】 30
解：∵△ABC≌△FDE，
∴∠BAC=∠F=105°，
∵∠BAC+∠B+∠C=180°，
∴∠B=180°-105°-45°=30°．
故答案为30．
13.【答案】 22.5
解：∵AD为BC边上的高，且AD＝BD，
∴∠ABD＝∠BAD＝45°，
∵AB＝BC，
∴∠BAC＝ ＝67.5°，
∴∠3＝∠BAC－∠BAD＝67.5°－45°＝22.5°，
故填：22.5°．
14.【答案】 ①、②、④
解：如下图
①∵∠ACB=60°，∴∠ACM=120°
∵CE是∠ACM的角平分线，∴∠ACE=∠ECM=60°
∴∠ACB=∠ACE
∵BC=DC，AC=CE
∴△ABC≌△EDC(SAS)，正确；
②∵CF=CG，已知∠BCF=∠DCG=60°，BC=DC
∴△BCF≌△DCG
∴∠FBC=∠GDC
∵∠BFC=∠DFH
∴∠BCF=∠DHF=60°，正确；
③条件不足，无法得出 ，错误；
④∵BE是∠DEC的角平分线，
∴∠DEF=∠CEF
∵∠ECM=∠CBF+∠FEC=60°，∠DCM=∠A+∠ABC=120°
∴∠A+∠ABC=2(∠FBC+∠FEC)=2∠FBC+2∠FEC=2∠FBC+∠DEC
∵∠DEC=∠A
∴∠ABC=2∠FBC
∴BE平分∠ABC，正确；
故答案为：①②④.
15.【答案】 4或6
解：设点Q的速度为x，则运动t秒时，CQ=xt，P点的速度为4，则BC=16
∴BP=4t，PPC=（16-4t）
又∵AB=AC=24，点D为AB的中点
∴BD=AB=12
∵∠B=∠C
∴运动t秒时，△BPD与△CQP全等共有两种情况
①当△BPD≌△CQP时，
则有BD=CP，BP=CQ
即12=16-4t，4t=xt
即t=1
∴由4t=xt可知，x=4
②当△BPD≌△CPQ时，
则有BD=CQ，BP=CP
即12=xt，4t=16-4t
∴t=2，x=6
16.【答案】 18或70
解：设BE=3t，则BF=7t，因为∠A=∠B=90°，使△AEG与△BEF全等，可分两种情况：
情况一：当BE=AG，BF=AE时，
∵BF=AE，AB=60，
∴7t=60-3t，
解得：t=6，
∴AG=BE=3t=3×6=18；
情况二：当BE=AE，BF=AG时，
∵BE=AE，AB=60，
∴3t=60-3t，
解得：t=10，
∴AG=BF=7t=7×10=70，
综上所述，AG=18或AG=70.
故答案为：18或70.
三、解答题
17.【答案】 解：若添加条件为：BC=CD,证明如下：
在△ABC和△ADC中
∴△ABC≌△ADC（SSS）（答案不唯一）．
18.【答案】 解：∵△ABD≌△ACE，
∴AD=AE，AB=AC，
∴BE=AB-AE=AC-AD=CD．
19.【答案】 证明：∵AB∥DE，
∴∠A＝∠D，
∵AF＝DC，
∴AC＝DF．
∴在△ABC与△DEF中 ，
∴△ABC≌△DEF（SAS），
∴BC=EF．
20.【答案】 解：在△ABC中，∵∠A＝85°，∠B＝60°，
∴∠ACB=180°－∠A－∠B=180°－85°－60°=35°，
∵△DEF≌△ABC，
∴∠F=∠ACB=35°，DE=AB=8，
∵EH=2，
∴DH=DE―EH=8-2=6.
21.【答案】 解： ， ，
，
在 和 中， ， ≌ ，
，
故测得 米，即可知道AB也为15米.
22.【答案】 证明：∵AE=CF，
∴AE-EF=CF- EF，
∴AF=CE
在△ADF和△CBE中
∴△ADF≌△CBE(SSS)
23.【答案】 证明：∵D是BC的中点，
∴BD=CD，
∵DE⊥AB，DF⊥AC，
∴∠BED=∠CFD=90°，
又∵∠BDE=∠CDF ，
∴△BDE≌△CDF(AAS)，
∴DE= DF，
∴点D在∠BAC的平分线上，
∴AD平分∠BAC
24.【答案】 解： AC⊥BD，EF⊥BD，
，
在 和 中，
?，
? ≌ ，
，
．
25.【答案】 解：如图，在线段CD上截取DE=BD，
∵AD=AD，∠ADB=∠ADE，BD=DE
∴△ADB≌△ADE（SAS）
∴AE=AB，∠ABC=∠AED，
∴AB+BD=AE+DE，
∵AB+BD=CD，
∴CD=AE+DE，
∵CD=CE+DE，
∴AE=CE
∴∠C=∠CAE，
∴∠AED=∠C+∠CAE=2∠C，
∴ ．
26.【答案】 解：如图所示，
△APQ的周长为2，即AP+AQ+PQ=2①，
正方形ABCD的边长是1，即AQ+QD=1，AP+PB=1，
∴AP+AQ+QD+PB=2②，
①-②得，PQ-QD-PB=0，
∴PQ=PB+QD．
延长AB至M，使BM=DQ．连接CM，△CBM≌△CDQ（SAS），
∴∠BCM=∠DCQ，CM=CQ，
∵∠DCQ+∠QCB=90°，
∴∠BCM+∠QCB=90°，即∠QCM=90°，
PM=PB+BM=PB+DQ=PQ．
在△CPQ与△CPM中，
CP=CP，PQ=PM，CQ=CM，
∴△CPQ≌△CPM（SSS），
∴∠PCQ=∠PCM= ∠QCM=45°．