六年级数学下册试题 一课一练《图形与几何-立体图形的体积和容积》 -苏教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《图形与几何-立体图形的体积和容积》 -苏教版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 400.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 08:34:51 | ||
图片预览



文档简介
《图形与几何-立体图形的体积和容积》
一.选择题
1.将直角三角形以为轴旋转一周,得到的圆锥体积是,那么
A.
B.
C.
D.
2.把一团圆柱体橡皮泥揉成与它等底的圆锥体,高将
A.扩大3倍
B.缩小3倍
C.扩大6倍
3.一个体积是的圆锥,半径是,它的高是 .
A.2
B.8
C.6
4.一个圆锥和一个圆柱的高相等,圆锥底面半径是1厘米,圆柱底面半径是2厘米,圆锥体积是圆柱体积的
A.
B.
C.
D.
二.填空题
1.如图是一个直角三角形,以的直角边所在直线为轴旋转一周,所得到的图形是 ,它的体积是 .
2.计算下面圆锥的体积是
3.一个圆锥形零件的底面半径是4厘米,高是9厘米,它的体积是 立方厘米.
4.下面,以直角三角形的斜边为轴旋转一圈,求所形成图形的体积是
.(得数保留整数)
5.一个圆柱形水桶,里面盛48升的水,正好盛满,如果把一块与水桶等底等高的圆锥形,放入水中,桶内还有
升水.
6.一个正方体木料削成最大的圆锥,圆锥的体积占正方体的
.
三.判断题
1.在一个圆柱中挖去一个最大的圆锥,剩下部分的体积是圆柱的.(
)
2.把一个圆柱削成一个圆锥,这个圆锥的体积是圆柱体积的.(
)
3.把一个圆柱削成最大的圆锥体,削去部分的体积与圆锥的体积的比是.(
)
4.把圆柱体削成一个最大的圆锥体,圆锥体体积是削去部分的.(
)
四.计算题
1.求如图图形的体积.单位:厘米.
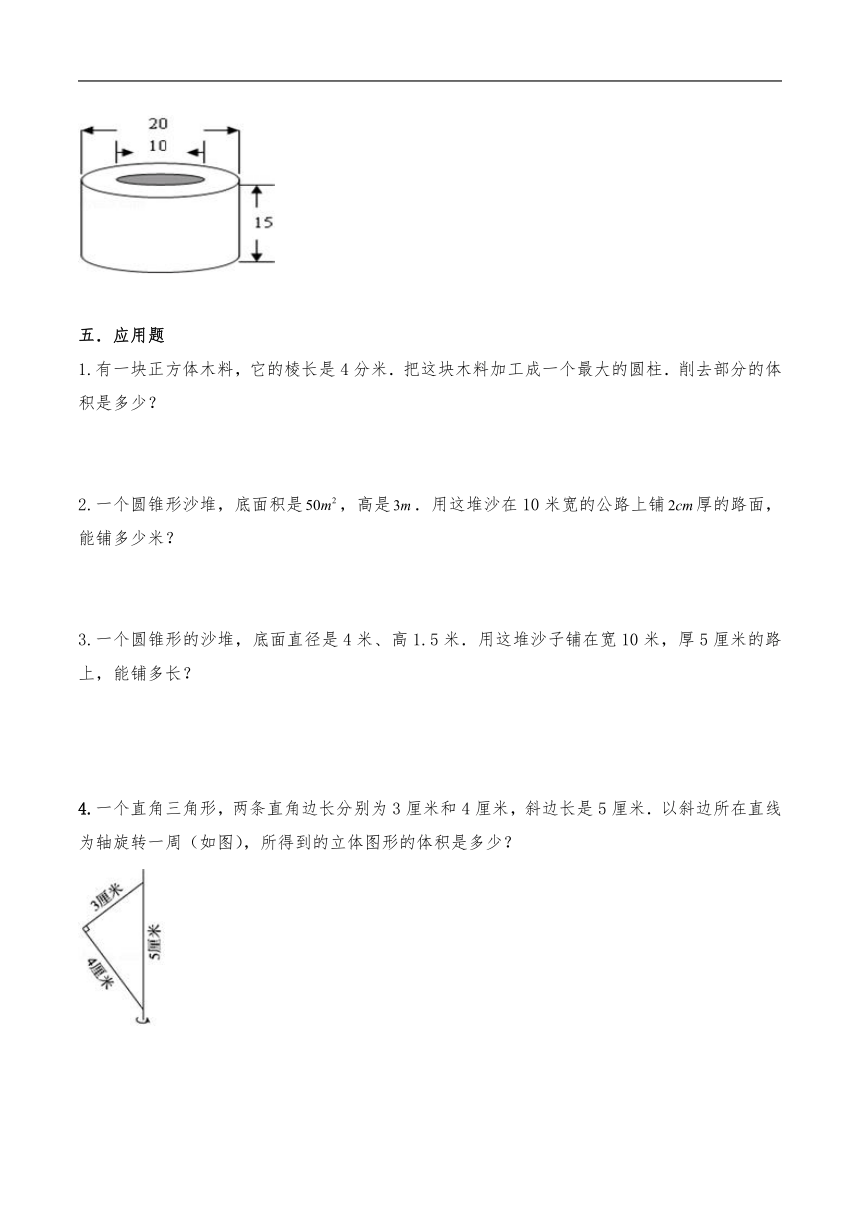
2.求如图空心圆柱的表面积.(单位:分米)
3.求立体图形的体积
单位(分米)
五.应用题
1.有一块正方体木料,它的棱长是4分米.把这块木料加工成一个最大的圆柱.削去部分的体积是多少?
2.一个圆锥形沙堆,底面积是,高是.用这堆沙在10米宽的公路上铺厚的路面,能铺多少米?
3.一个圆锥形的沙堆,底面直径是4米、高1.5米.用这堆沙子铺在宽10米,厚5厘米的路上,能铺多长?
4.一个直角三角形,两条直角边长分别为3厘米和4厘米,斜边长是5厘米.以斜边所在直线为轴旋转一周(如图),所得到的立体图形的体积是多少?
5.一个底面半径与高的比为的圆锥体煤堆.高是6米,如果每0.75立方米的煤是1吨,这堆煤有多少吨?
6.一个圆锥形麦堆,高1.2米,占地面积16平方米,如果每立方米小麦重750千克,这堆小麦重多少千克?
7.小红和小军分别以直角梯形的上底和下底为轴,将梯形旋转一周,得到两个立体图形.
(1)你同意谁的说法,请将名字填在横线里.
(2)甲、乙两个立体图形的体积比是多少?(写出你的思考过程)
8.工地上有一些沙子,堆起来近似于一个圆锥.如果每立方米沙重,这堆沙重多少吨?(得数保留一位小数.
9.一个装满稻谷的粮囤,上面是圆锥形,下面是圆柱形,量得圆柱地面的周长是,高是,圆锥的高是,这个粮囤能装稻谷多少立方米?如果
每立方米稻谷重500千克,这个粮囤能装稻谷多少千克?
10.绕一个直角三角形(如图)的短直角边旋转一周,得到一个立体图形.(单位:厘米)
(1)这个立体图形是什么?
(2)这个立体图形的体积是多少?
11.一个圆锥形的沙石堆,底面积是188.4平方米,高15米.如果用这堆沙石铺路,公路宽10米.沙石厚2分米,能铺多少米长?
12.一个粮囤,上面是圆锥,下面是圆柱形(如图).如果每立方米的粮食重600千克,这个粮囤可囤粮食多少千克?
13.去超市买酸奶,发现一种酸奶采用长方体塑封纸盒包装,从外面量这种纸盒长6.4厘米,宽4厘米,高8.5厘米.这种酸奶盒上标注酸奶的净含量为220毫升,标注是否真实?
14.一个谷囤的形状如图,下面是圆柱形,底面周长是18.84米,高是2米;上面是圆锥形,高是1.5米.这个谷囤最多能装稻谷多少立方米?
答案
一.选择题
1..2..3..4..
二.填空题
1.圆锥、25.12.
2.50.
3.150.72.
4.30.144立方厘米.
5.32.
6..
三.判断题
1..2..3..4.√.
四.计算题
1.解:
(立方厘米),
答:它的体积是11860立方厘米.
2.解:
(平方分米),
答:这个空心圆柱的表面积是94.2平方分米.
3.解:
(立方分米),
答:这个立体图形的体积是3532.5立方分米.
五.应用题
1.解:
(立方分米),
答:削去部分的体积是13.76立方分米.
2.解:2厘米米,
(米,
答:能铺250米.
3.解:5厘米米
(米
答:能铺12.56米.
4.解:直角三角形斜边所在直线为轴旋转一周,得到的几何体是同一底面的两个圆锥,如上图所示,
设这个圆锥的底面半径是,则:
,
,
,
所以这个立体图形的体积是:
,
;
(立方厘米),
答:旋转一周后的立体图形的体积是30.144立方厘米.
5.解:
(立方米)
(吨
答:这堆煤有吨.
6.解:,
,
(千克).
答:这堆小麦重4800千克.
7.解:(1)我同意小红的说法,分别以直角梯形的上底和下底为轴,将梯形旋转一周,得到两个立体图形的体积不相等.以梯形的上底为轴旋转得到是高为6厘米,底面半径是3厘米的圆柱内有一个空心圆锥;而以梯形的下底为轴旋转得到的是上面是圆锥、下面是圆柱.
(2)甲的体积:
(立方厘米);
乙的体积:
(立方厘米);
.
答:甲、乙体积的比是.
故答案为:小红.
8.解:
(吨,
答:这堆沙重10.1吨.
9.解:(1)圆柱的底面积为:
(平方米);
这个粮囤的体积:
(立方米);
答:这个粮囤能装稻谷7.85立方米.
(2)(千克)
答:这个粮囤最多能装稻谷3925千克.
10.解:以直角三角形短直角边为轴旋转一周得到一个底面半径是5厘米,高是4厘米的圆锥.所以这个立体图形是圆锥.
(2)
(立方厘米),
答:这个立体图形的体积是立方厘米.
11.解:2分米米
(米
答:能铺471米长.
12.解:这个粮囤的底面积是:
(平方米)
这个粮囤的体积是:
(立方米)
这囤小麦的重量是:
(千克).
答:这个粮囤可囤粮食18840千克.
13.解:(立方厘米)(毫升);
答:盒子的体积是217毫升,而净含量为220毫升,不真实.
14.解:
(立方米);
答:这个谷囤最多能装稻谷70.65立方米.
一.选择题
1.将直角三角形以为轴旋转一周,得到的圆锥体积是,那么
A.
B.
C.
D.
2.把一团圆柱体橡皮泥揉成与它等底的圆锥体,高将
A.扩大3倍
B.缩小3倍
C.扩大6倍
3.一个体积是的圆锥,半径是,它的高是 .
A.2
B.8
C.6
4.一个圆锥和一个圆柱的高相等,圆锥底面半径是1厘米,圆柱底面半径是2厘米,圆锥体积是圆柱体积的
A.
B.
C.
D.
二.填空题
1.如图是一个直角三角形,以的直角边所在直线为轴旋转一周,所得到的图形是 ,它的体积是 .
2.计算下面圆锥的体积是
3.一个圆锥形零件的底面半径是4厘米,高是9厘米,它的体积是 立方厘米.
4.下面,以直角三角形的斜边为轴旋转一圈,求所形成图形的体积是
.(得数保留整数)
5.一个圆柱形水桶,里面盛48升的水,正好盛满,如果把一块与水桶等底等高的圆锥形,放入水中,桶内还有
升水.
6.一个正方体木料削成最大的圆锥,圆锥的体积占正方体的
.
三.判断题
1.在一个圆柱中挖去一个最大的圆锥,剩下部分的体积是圆柱的.(
)
2.把一个圆柱削成一个圆锥,这个圆锥的体积是圆柱体积的.(
)
3.把一个圆柱削成最大的圆锥体,削去部分的体积与圆锥的体积的比是.(
)
4.把圆柱体削成一个最大的圆锥体,圆锥体体积是削去部分的.(
)
四.计算题
1.求如图图形的体积.单位:厘米.
2.求如图空心圆柱的表面积.(单位:分米)
3.求立体图形的体积
单位(分米)
五.应用题
1.有一块正方体木料,它的棱长是4分米.把这块木料加工成一个最大的圆柱.削去部分的体积是多少?
2.一个圆锥形沙堆,底面积是,高是.用这堆沙在10米宽的公路上铺厚的路面,能铺多少米?
3.一个圆锥形的沙堆,底面直径是4米、高1.5米.用这堆沙子铺在宽10米,厚5厘米的路上,能铺多长?
4.一个直角三角形,两条直角边长分别为3厘米和4厘米,斜边长是5厘米.以斜边所在直线为轴旋转一周(如图),所得到的立体图形的体积是多少?
5.一个底面半径与高的比为的圆锥体煤堆.高是6米,如果每0.75立方米的煤是1吨,这堆煤有多少吨?
6.一个圆锥形麦堆,高1.2米,占地面积16平方米,如果每立方米小麦重750千克,这堆小麦重多少千克?
7.小红和小军分别以直角梯形的上底和下底为轴,将梯形旋转一周,得到两个立体图形.
(1)你同意谁的说法,请将名字填在横线里.
(2)甲、乙两个立体图形的体积比是多少?(写出你的思考过程)
8.工地上有一些沙子,堆起来近似于一个圆锥.如果每立方米沙重,这堆沙重多少吨?(得数保留一位小数.
9.一个装满稻谷的粮囤,上面是圆锥形,下面是圆柱形,量得圆柱地面的周长是,高是,圆锥的高是,这个粮囤能装稻谷多少立方米?如果
每立方米稻谷重500千克,这个粮囤能装稻谷多少千克?
10.绕一个直角三角形(如图)的短直角边旋转一周,得到一个立体图形.(单位:厘米)
(1)这个立体图形是什么?
(2)这个立体图形的体积是多少?
11.一个圆锥形的沙石堆,底面积是188.4平方米,高15米.如果用这堆沙石铺路,公路宽10米.沙石厚2分米,能铺多少米长?
12.一个粮囤,上面是圆锥,下面是圆柱形(如图).如果每立方米的粮食重600千克,这个粮囤可囤粮食多少千克?
13.去超市买酸奶,发现一种酸奶采用长方体塑封纸盒包装,从外面量这种纸盒长6.4厘米,宽4厘米,高8.5厘米.这种酸奶盒上标注酸奶的净含量为220毫升,标注是否真实?
14.一个谷囤的形状如图,下面是圆柱形,底面周长是18.84米,高是2米;上面是圆锥形,高是1.5米.这个谷囤最多能装稻谷多少立方米?
答案
一.选择题
1..2..3..4..
二.填空题
1.圆锥、25.12.
2.50.
3.150.72.
4.30.144立方厘米.
5.32.
6..
三.判断题
1..2..3..4.√.
四.计算题
1.解:
(立方厘米),
答:它的体积是11860立方厘米.
2.解:
(平方分米),
答:这个空心圆柱的表面积是94.2平方分米.
3.解:
(立方分米),
答:这个立体图形的体积是3532.5立方分米.
五.应用题
1.解:
(立方分米),
答:削去部分的体积是13.76立方分米.
2.解:2厘米米,
(米,
答:能铺250米.
3.解:5厘米米
(米
答:能铺12.56米.
4.解:直角三角形斜边所在直线为轴旋转一周,得到的几何体是同一底面的两个圆锥,如上图所示,
设这个圆锥的底面半径是,则:
,
,
,
所以这个立体图形的体积是:
,
;
(立方厘米),
答:旋转一周后的立体图形的体积是30.144立方厘米.
5.解:
(立方米)
(吨
答:这堆煤有吨.
6.解:,
,
(千克).
答:这堆小麦重4800千克.
7.解:(1)我同意小红的说法,分别以直角梯形的上底和下底为轴,将梯形旋转一周,得到两个立体图形的体积不相等.以梯形的上底为轴旋转得到是高为6厘米,底面半径是3厘米的圆柱内有一个空心圆锥;而以梯形的下底为轴旋转得到的是上面是圆锥、下面是圆柱.
(2)甲的体积:
(立方厘米);
乙的体积:
(立方厘米);
.
答:甲、乙体积的比是.
故答案为:小红.
8.解:
(吨,
答:这堆沙重10.1吨.
9.解:(1)圆柱的底面积为:
(平方米);
这个粮囤的体积:
(立方米);
答:这个粮囤能装稻谷7.85立方米.
(2)(千克)
答:这个粮囤最多能装稻谷3925千克.
10.解:以直角三角形短直角边为轴旋转一周得到一个底面半径是5厘米,高是4厘米的圆锥.所以这个立体图形是圆锥.
(2)
(立方厘米),
答:这个立体图形的体积是立方厘米.
11.解:2分米米
(米
答:能铺471米长.
12.解:这个粮囤的底面积是:
(平方米)
这个粮囤的体积是:
(立方米)
这囤小麦的重量是:
(千克).
答:这个粮囤可囤粮食18840千克.
13.解:(立方厘米)(毫升);
答:盒子的体积是217毫升,而净含量为220毫升,不真实.
14.解:
(立方米);
答:这个谷囤最多能装稻谷70.65立方米.
