2021年人教版八年级数学下册 19.1《函数》同步练习(Word版 含解析)
文档属性
| 名称 | 2021年人教版八年级数学下册 19.1《函数》同步练习(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 115.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 18:07:36 | ||
图片预览


文档简介
2021年人教版八年级下册19.1《函数》同步练习
一.选择题
1.下列曲线中表示y是x的函数的是( )
A.B.C.D.
2.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.π,r D.C,2π
3.在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.s、v是变量 B.s、t是变量
C.v、t是变量 D.s、v、t都是变量
4.在函数中,y=自变量x的取值范围是( )
A.x≥2 B.x>2 C.x≠2 D.x<2
5.正方体的棱长为x,表面积为y,则y与x之间的函数关系式为( )
A.y=x B.y=6x C.y=6x2 D.y=
6.某汽车的油箱一次加满汽油50升,可行驶y千米(假设汽油能行驶至油用完),设该汽车行驶每100千米耗油x升,则y关于x的函数表达式为( )
A.y=2x B.y= C.y=5000x D.y=
7.变量x,y的一些对应值如表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 9 2 1 0 ﹣7 ﹣26 …
根据表格中的数据规律,当x=﹣5时,y的值是( )
A.76 B.﹣74 C.126 D.﹣124
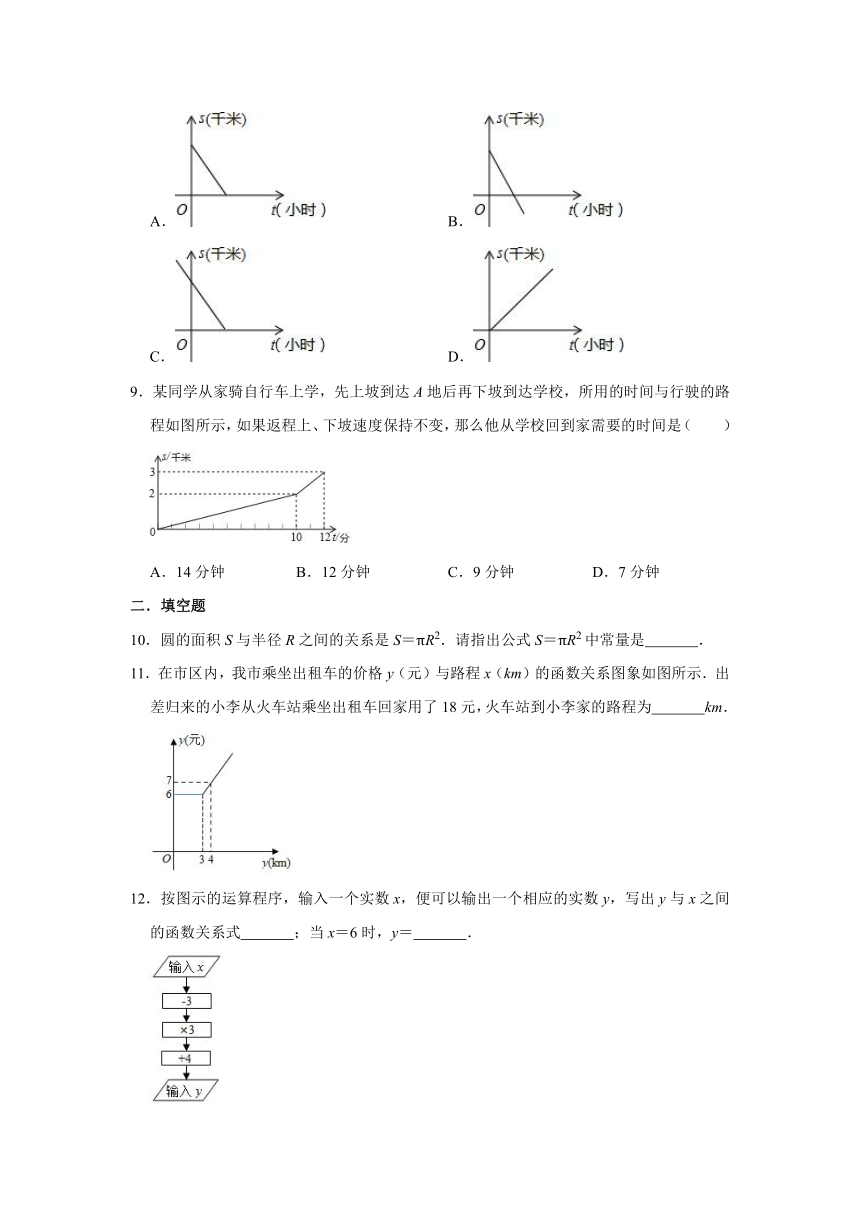
8.一辆客车从酒泉出发开往兰州,设客车出发t小时后与兰州的距离为s千米,下列图象能大致反映s与t之间的函数关系的是( )
A. B.
C. D.
9.某同学从家骑自行车上学,先上坡到达A地后再下坡到达学校,所用的时间与行驶的路程如图所示,如果返程上、下坡速度保持不变,那么他从学校回到家需要的时间是( )
A.14分钟 B.12分钟 C.9分钟 D.7分钟
二.填空题
10.圆的面积S与半径R之间的关系是S=πR2.请指出公式S=πR2中常量是 .
11.在市区内,我市乘坐出租车的价格y(元)与路程x(km)的函数关系图象如图所示.出差归来的小李从火车站乘坐出租车回家用了18元,火车站到小李家的路程为 km.
12.按图示的运算程序,输入一个实数x,便可以输出一个相应的实数y,写出y与x之间的函数关系式 ;当x=6时,y= .
13.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离s(单位:米)与时间t(单位:分钟)的对应关系如图所示,则文具店与小张家的距离为 .
三.解答题
14.“十一”期间,小明和父母一起开车到距家200km的景点旅游,出发前,汽车油箱内储油45L,当行驶150km时,发现油箱余油量为30L.(假设行驶过程中汽车的耗油量是均匀的)
(1)求该车平均每千米的耗油量,并写出行驶路程x(km)与剩余油量Q(L)的关系式;
(2)当x=280时,求剩余油量Q.
15.2020年,周至县小李家的猕猴桃喜获丰收.在销售过程中,猕猴桃的销售额y(元)与销量x(千克)满足如下关系:
销售量x(千克) 1 2 3 4 5 6 7 8
销售额y(元) 6 12 18 24 30 36 42 48
(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为 ;
(3)当猕猴桃销售量为100千克时,销售额是多少元?
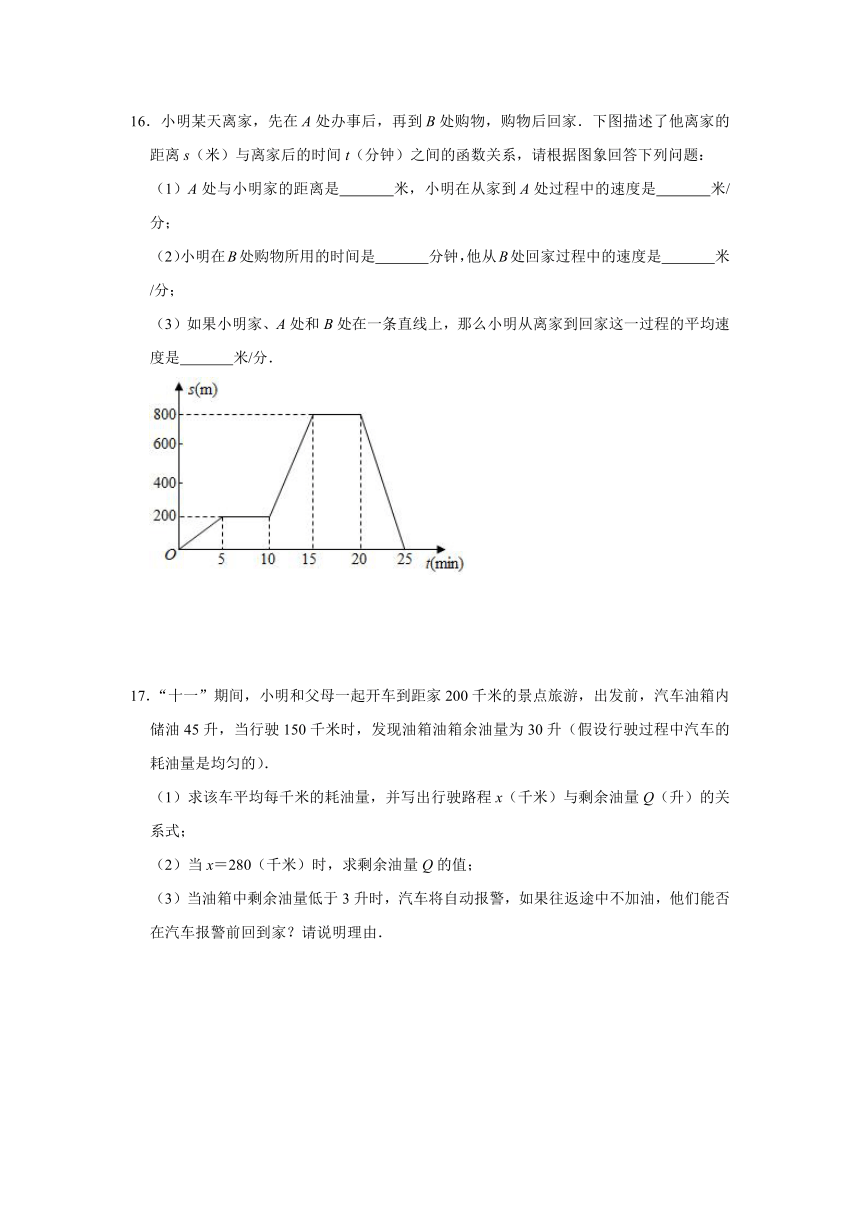
16.小明某天离家,先在A处办事后,再到B处购物,购物后回家.下图描述了他离家的距离s(米)与离家后的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
(1)A处与小明家的距离是 米,小明在从家到A处过程中的速度是 米/分;
(2)小明在B处购物所用的时间是 分钟,他从B处回家过程中的速度是 米/分;
(3)如果小明家、A处和B处在一条直线上,那么小明从离家到回家这一过程的平均速度是 米/分.
17.“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
18.小明家所在地的供电公司实行“峰谷电价”,峰时(8:00~21:00)电价为0.5元/度,谷时(21:00~8:00)电价为0.3元/度.为了解空调制暖的耗能情况,小明记录了家里某天0时~24时内空调制暖的用电量,其用电量y(度)与时间x(h)的函数关系如图所示.
(1)小明家白天不开空调的时间共 h;
(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为w元,请画出该天0时~24时内w与x的函数图象.(标注必要数据)
参考答案
一.选择题
1.解:A、不能表示y是x的函数,故此选项不合题意;
B、不能表示y是x的函数,故此选项不合题意;
C、不能表示y是x的函数,故此选项合题意;
D、能表示y是x的函数,故此选项不符合题意;
故选:C.
2.解:在圆周长的计算公式C=2πr中,变量有C和r,
故选:B.
3.解:在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则v、t是变量,s是常量,
故选:C.
4.解:由题意得,x﹣2≥0,
解得,x≥2,
故选:A.
5.解:由题意得,y=6x2,
故选:C.
6.解:∵该汽车行驶每100千米耗油x升,
∴1升汽油可走千米,
∴y=50×=,
∴y关于x的函数表达式为y=,
故选:D.
7.解:根据表格数据可知,函数的解析式为y=﹣x3+1,
当x=﹣5时,y=﹣(﹣5)3+1=126.
故选:C.
8.解:根据出发时与终点这两个特殊点的意义,图象能大致反映s与t之间的函数关系的是应选A.
故选:A.
9.解:由图象可知,该同学上坡的速度为:(千米/分钟),下坡的速度为:(千米/分钟),
则他从学校回到家需要的时间是:(分钟).
故选:C.
二.填空题
10.解:公式S=πR2中常量是π,
故答案为:π.
11.解:由题意可知,当x≤3时,出租车收费为6元,超出3km时,每千米收费为:(7﹣6)÷(4﹣3)=1(元),
所以火车站到小李家的路程为:3+(18﹣6)÷1=15(km ).
故答案为:15.
12.解:由题意得,
y=3(x﹣3)+4
=3x﹣5,
把x=6代入y=3x﹣5得,
y=13.
故答案为:y=3x﹣5,13.
13.解:小张骑车的速度=1500÷(6﹣1)=300米/分钟.
文具店与小张家的距离=1500﹣300×2=900米.
故答案为:900米.
三.解答题
14.解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(L/km),
行驶路程x(km)与剩余油量Q(L)的关系式为Q=45﹣0.1x.
(2)当x=280时,Q=45﹣0.1×280=17.
故当x=280时,剩余油量Q为17L.
故答案为:(1)Q=45﹣0.1x.(2)当x=280时,剩余油量Q为17L.
15.解:(1)在这个变化过程中,自变量是猕猴桃的销量,因变量是猕猴桃的销售额,
故答案为:猕猴桃的销量,猕猴桃的销售额;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为y=6x,
故答案为:y=6x;
(3)将x=100代入y=6x,可得y=6×100=600,
答:当猕猴桃销售量为100千克时,销售额是600元.
16.解:(1)由图可知,x=5时小明到达A处,A处离家距离为200米;
200÷5=40(米/分).
(2)10﹣5=5(分);
800÷(25﹣20)=160(米/分).
(3)小明往返所走路程为800×2=1600(米),往返所用时间为25分.
∴1600÷25=64(米/分).
故答案为:(1)200,40;
(2)5,160;
(3)64.
17.解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(升/千米),
行驶路程x(千米)与剩余油量Q(升)的关系式为Q=45﹣0.1x;
(2)当x=280时,Q=45﹣0.1×280=17(L).
答:当x=280(千米)时,剩余油量Q的值为17L.
(3)(45﹣3)÷0.1=420(千米),
∵420>400,
∴他们能在汽车报警前回到家.
18.解:(1)小明家白天不开空调的时间为:18﹣8=10(h),
故答案为:10;
(2)峰时所用电费为:3×3×0.5=4.5(元),
谷时所用电费为:11×3×0.3=9.9(元),
所以小明家该天空调制暖所用的电费为:4.5+9.9=14.4(元);
(3)根据题意,可得该天0时~24时内w与x的函数图象如下:
一.选择题
1.下列曲线中表示y是x的函数的是( )
A.B.C.D.
2.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.π,r D.C,2π
3.在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则下列说法正确的是( )
A.s、v是变量 B.s、t是变量
C.v、t是变量 D.s、v、t都是变量
4.在函数中,y=自变量x的取值范围是( )
A.x≥2 B.x>2 C.x≠2 D.x<2
5.正方体的棱长为x,表面积为y,则y与x之间的函数关系式为( )
A.y=x B.y=6x C.y=6x2 D.y=
6.某汽车的油箱一次加满汽油50升,可行驶y千米(假设汽油能行驶至油用完),设该汽车行驶每100千米耗油x升,则y关于x的函数表达式为( )
A.y=2x B.y= C.y=5000x D.y=
7.变量x,y的一些对应值如表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 9 2 1 0 ﹣7 ﹣26 …
根据表格中的数据规律,当x=﹣5时,y的值是( )
A.76 B.﹣74 C.126 D.﹣124
8.一辆客车从酒泉出发开往兰州,设客车出发t小时后与兰州的距离为s千米,下列图象能大致反映s与t之间的函数关系的是( )
A. B.
C. D.
9.某同学从家骑自行车上学,先上坡到达A地后再下坡到达学校,所用的时间与行驶的路程如图所示,如果返程上、下坡速度保持不变,那么他从学校回到家需要的时间是( )
A.14分钟 B.12分钟 C.9分钟 D.7分钟
二.填空题
10.圆的面积S与半径R之间的关系是S=πR2.请指出公式S=πR2中常量是 .
11.在市区内,我市乘坐出租车的价格y(元)与路程x(km)的函数关系图象如图所示.出差归来的小李从火车站乘坐出租车回家用了18元,火车站到小李家的路程为 km.
12.按图示的运算程序,输入一个实数x,便可以输出一个相应的实数y,写出y与x之间的函数关系式 ;当x=6时,y= .
13.小张骑车从图书馆回家,中途在文具店买笔耽误了1分钟,然后继续骑车回家.若小张骑车的速度始终不变,从出发开始计时,小张离家的距离s(单位:米)与时间t(单位:分钟)的对应关系如图所示,则文具店与小张家的距离为 .
三.解答题
14.“十一”期间,小明和父母一起开车到距家200km的景点旅游,出发前,汽车油箱内储油45L,当行驶150km时,发现油箱余油量为30L.(假设行驶过程中汽车的耗油量是均匀的)
(1)求该车平均每千米的耗油量,并写出行驶路程x(km)与剩余油量Q(L)的关系式;
(2)当x=280时,求剩余油量Q.
15.2020年,周至县小李家的猕猴桃喜获丰收.在销售过程中,猕猴桃的销售额y(元)与销量x(千克)满足如下关系:
销售量x(千克) 1 2 3 4 5 6 7 8
销售额y(元) 6 12 18 24 30 36 42 48
(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为 ;
(3)当猕猴桃销售量为100千克时,销售额是多少元?
16.小明某天离家,先在A处办事后,再到B处购物,购物后回家.下图描述了他离家的距离s(米)与离家后的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
(1)A处与小明家的距离是 米,小明在从家到A处过程中的速度是 米/分;
(2)小明在B处购物所用的时间是 分钟,他从B处回家过程中的速度是 米/分;
(3)如果小明家、A处和B处在一条直线上,那么小明从离家到回家这一过程的平均速度是 米/分.
17.“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
18.小明家所在地的供电公司实行“峰谷电价”,峰时(8:00~21:00)电价为0.5元/度,谷时(21:00~8:00)电价为0.3元/度.为了解空调制暖的耗能情况,小明记录了家里某天0时~24时内空调制暖的用电量,其用电量y(度)与时间x(h)的函数关系如图所示.
(1)小明家白天不开空调的时间共 h;
(2)求小明家该天空调制暖所用的电费;
(3)设空调制暖所用电费为w元,请画出该天0时~24时内w与x的函数图象.(标注必要数据)
参考答案
一.选择题
1.解:A、不能表示y是x的函数,故此选项不合题意;
B、不能表示y是x的函数,故此选项不合题意;
C、不能表示y是x的函数,故此选项合题意;
D、能表示y是x的函数,故此选项不符合题意;
故选:C.
2.解:在圆周长的计算公式C=2πr中,变量有C和r,
故选:B.
3.解:在进行路程s、速度v和时间t的相关计算中,若保持行驶的路程不变,则v、t是变量,s是常量,
故选:C.
4.解:由题意得,x﹣2≥0,
解得,x≥2,
故选:A.
5.解:由题意得,y=6x2,
故选:C.
6.解:∵该汽车行驶每100千米耗油x升,
∴1升汽油可走千米,
∴y=50×=,
∴y关于x的函数表达式为y=,
故选:D.
7.解:根据表格数据可知,函数的解析式为y=﹣x3+1,
当x=﹣5时,y=﹣(﹣5)3+1=126.
故选:C.
8.解:根据出发时与终点这两个特殊点的意义,图象能大致反映s与t之间的函数关系的是应选A.
故选:A.
9.解:由图象可知,该同学上坡的速度为:(千米/分钟),下坡的速度为:(千米/分钟),
则他从学校回到家需要的时间是:(分钟).
故选:C.
二.填空题
10.解:公式S=πR2中常量是π,
故答案为:π.
11.解:由题意可知,当x≤3时,出租车收费为6元,超出3km时,每千米收费为:(7﹣6)÷(4﹣3)=1(元),
所以火车站到小李家的路程为:3+(18﹣6)÷1=15(km ).
故答案为:15.
12.解:由题意得,
y=3(x﹣3)+4
=3x﹣5,
把x=6代入y=3x﹣5得,
y=13.
故答案为:y=3x﹣5,13.
13.解:小张骑车的速度=1500÷(6﹣1)=300米/分钟.
文具店与小张家的距离=1500﹣300×2=900米.
故答案为:900米.
三.解答题
14.解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(L/km),
行驶路程x(km)与剩余油量Q(L)的关系式为Q=45﹣0.1x.
(2)当x=280时,Q=45﹣0.1×280=17.
故当x=280时,剩余油量Q为17L.
故答案为:(1)Q=45﹣0.1x.(2)当x=280时,剩余油量Q为17L.
15.解:(1)在这个变化过程中,自变量是猕猴桃的销量,因变量是猕猴桃的销售额,
故答案为:猕猴桃的销量,猕猴桃的销售额;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为y=6x,
故答案为:y=6x;
(3)将x=100代入y=6x,可得y=6×100=600,
答:当猕猴桃销售量为100千克时,销售额是600元.
16.解:(1)由图可知,x=5时小明到达A处,A处离家距离为200米;
200÷5=40(米/分).
(2)10﹣5=5(分);
800÷(25﹣20)=160(米/分).
(3)小明往返所走路程为800×2=1600(米),往返所用时间为25分.
∴1600÷25=64(米/分).
故答案为:(1)200,40;
(2)5,160;
(3)64.
17.解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(升/千米),
行驶路程x(千米)与剩余油量Q(升)的关系式为Q=45﹣0.1x;
(2)当x=280时,Q=45﹣0.1×280=17(L).
答:当x=280(千米)时,剩余油量Q的值为17L.
(3)(45﹣3)÷0.1=420(千米),
∵420>400,
∴他们能在汽车报警前回到家.
18.解:(1)小明家白天不开空调的时间为:18﹣8=10(h),
故答案为:10;
(2)峰时所用电费为:3×3×0.5=4.5(元),
谷时所用电费为:11×3×0.3=9.9(元),
所以小明家该天空调制暖所用的电费为:4.5+9.9=14.4(元);
(3)根据题意,可得该天0时~24时内w与x的函数图象如下:
