2020-2021学年七年级数学人教版下册:第五章:相交线与平行线复习课件(共22张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册:第五章:相交线与平行线复习课件(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 882.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 19:03:31 | ||
图片预览




文档简介
(共22张PPT)
复习课
第五章:相交线与平行线
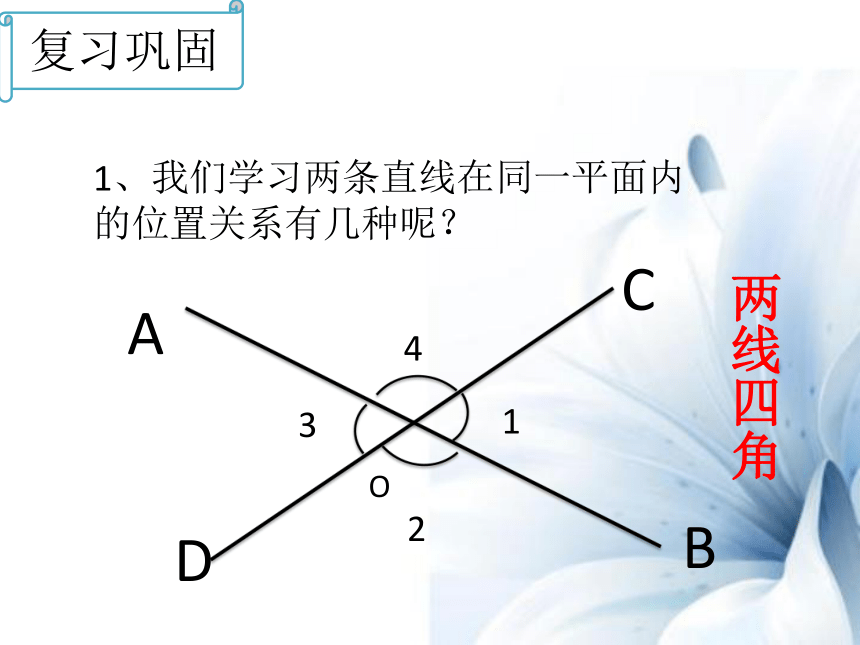
1、我们学习两条直线在同一平面内
的位置关系有几种呢?
复习巩固
A
O
D
C
B
4
2
3
1
两线四角
O
A
B
C
D
)
(
1
3
4
2
)
(
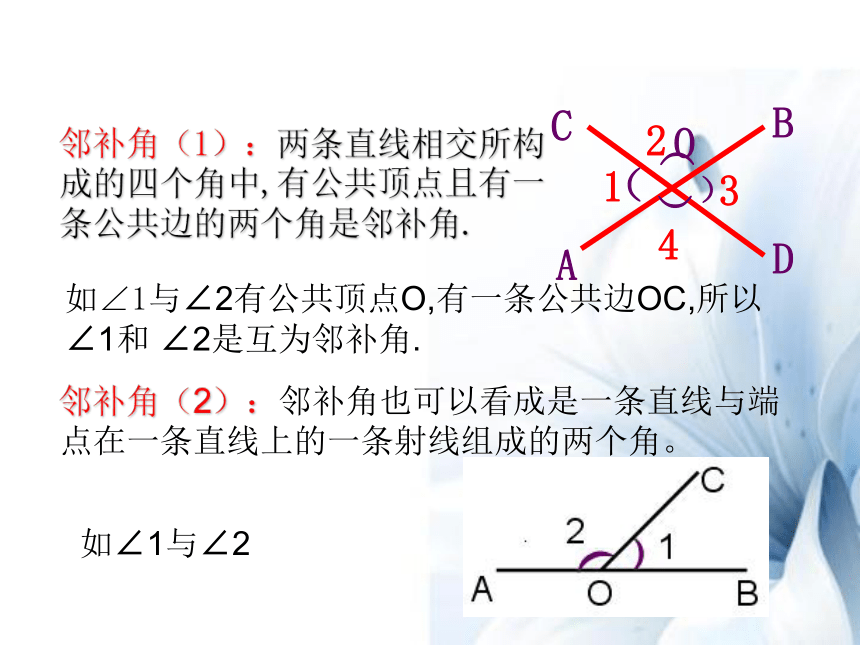
邻补角(1):两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角.
如∠1与∠2有公共顶点O,有一条公共边OC,所以∠1和
∠2是互为邻补角.
邻补角(2):邻补角也可以看成是一条直线与端点在一条直线上的一条射线组成的两个角。
如∠1与∠2
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
性质
邻补角互补
对顶角相等
相同点
都有一个公共顶点,它们都是成对出现的
不同点
对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个
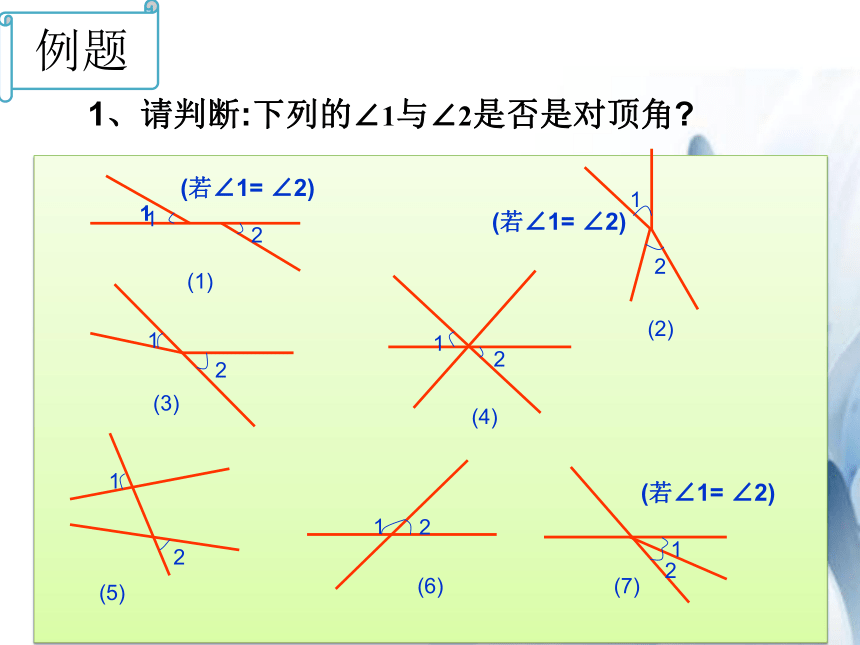
1、请判断:下列的∠1与∠2是否是对顶角?
1
2
1
2
1
2
1
2
1
2
1
2
1
1
2
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(若∠1=
∠2)
(若∠1=
∠2)
(若∠1=
∠2)
例题
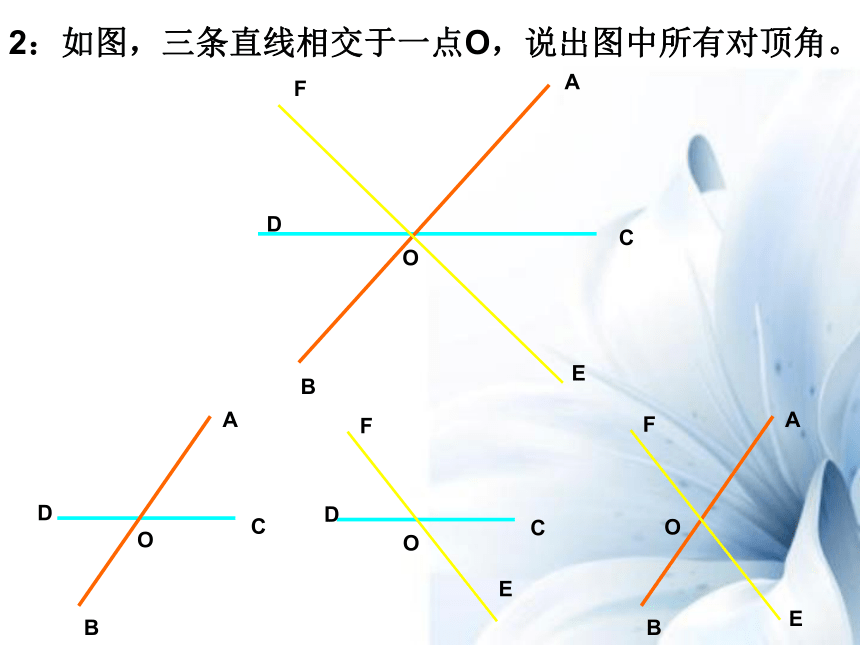
2:如图,三条直线相交于一点O,说出图中所有对顶角。
A
B
C
D
E
F
O
E
A
B
C
D
O
C
D
F
O
A
B
E
F
O
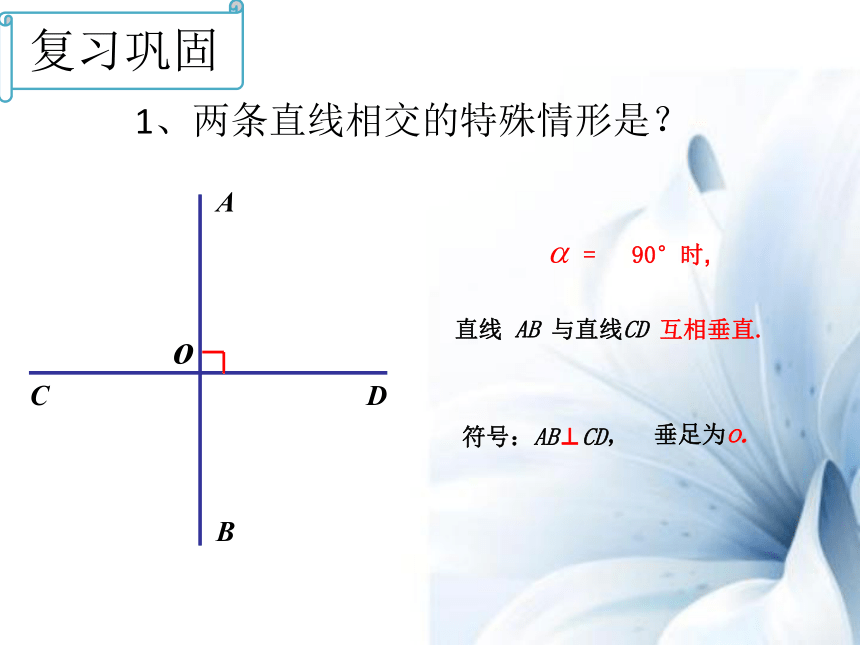
复习巩固
A
B
C
D
o
直线
AB
与直线CD
互相垂直.
=
90°时,
符号:AB⊥CD,
垂足为o.
1、两条直线相交的特殊情形是?
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线,即:
垂线的性质1:
过一点有且只有一条直线与已知直线垂直.
连接直线外一点与直线上各点的所有连线中,垂线段最短。
垂线的性质2:
垂线段最短
点到直线的距离:垂线段的长度
1、
过点
P
向线段
AB
所在直线引垂线,正确的是(
).
A
B
C
D
C
例题
2、
过点P作线段或射线所在直线的垂线
A
B
.
.
.P
(1)
.
O
.P
.A
(2)
A
C
E
B
D
O
1
∴
∠EOB=90°(垂直的定义)
∴
∠
EOD=
∠
EOB+
∠
BOD
=90
°+55
°=145
°
(
解:
∵
AB⊥OE
(已知)
∵
∠BOD=
∠1=55°
3、
如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
(对顶角相等)
复习巩固
角的名称
位置特征
基本图形
图形结构特征
同位角
在两条被截直线的______
在截线的______
形如字母___
在两条被截直线的______
在截线的______
形如字母___
在两条被截直线的______
在截线的_____
形如字母___
“F”
同旁
同侧
内错角
之间
两侧
“Z”
同旁内角
之间
同侧
“U”
a
7
8
5
3
2
6
4
1
c
b
1、找出图中的同位角、内错角
、同旁内角:
例题
复习巩固
1、平行线的概念
2、平行公理
3、平行公理的推广
在同一平面内,永不相交的两条直线叫做平行线
在同一平面内过直线外一点,有且只有一条直线与已知直线平行
如果两条直线都与第三条直线平行,那么这两条直线与互相平行。
复习巩固
1、平行线的判定
2、平行线的性质
1、同位角相等,两直线平行
2、内错角相等,两直线平行
3、同旁内角互补,两直线平行
1、两直线平行,同位角相等
2、两直线平行,内错角相等
3、两直线平行,同旁内角互补
例题
1、如图,AB∥CD,∠B=35°,
∠1=75°.求∠A的度数.
解:
因为AB∥CD,∠B=35°,
所以∠2
=
∠B=35°,
∠ACD
=
∠1+
∠2
=
35°+
75°=
110°.
又因为AB∥CD,所以∠A+
∠
ACD=
180°,
所以∠A=
180°-
∠
ACD=
70°.
2、如图所示,∠1=∠2,∠3=110°,求∠4.
解:
因为∠1=∠2,
所以a//b
(内错角相等,两直线平行),
所以∠3=∠4
(两直线平行,同位角相等).
又因为∠3=
110°,
3、如图,∠BHE与∠BGF互为补角,∠D=∠A.求证:∠B=∠C.
解:
∵∠BHE+
∠BGF=180°,
∴∠BGF=
∠BHA(同角的补角相等),
∴AE//DF(同位角相等,两直线平行),
∠BHE+
∠BHA=180°,
∴∠A=
∠BFD(两直线平行,同位角相等).
∵∠D=∠A,所以∠BFD=
∠D,
∴AB//CD(内错角相等,两直线平行).
∴∠B=∠C(两直线平行,内错角相等).
⌒
⌒
A
B
C
D
E
60°
32°
1
2
F
解:过E作EF//AB
因为AB//CD
所以EF//CD
所以∠1=∠B=60°
所以∠2=∠D=32°
所以∠BED=∠1+
∠2
=60°+
32°=
92°
4、
已知:如图AB∥CD,
∠ABE=
60°,
∠CDE=
32°,求∠BED的度数.
解:因为CE⊥AB,
DF⊥AB
所以DF//EC
所以∠BDF=∠1,
∠EDF=∠3
因为ED//AC,
所以∠3=∠2
所以∠EDF=∠2
又CE平分∠ACB
所以∠1=∠2
所以∠BDF=∠EDF
1
3
2
5、如图,在?ABC中,CE⊥AB于点E,DF⊥AB于点F,AC//ED,CE是∠ACB的平分线,则∠EDF=∠BDF,请说明理由。
书山有路勤为径
学海无涯苦做舟
复习课
第五章:相交线与平行线
1、我们学习两条直线在同一平面内
的位置关系有几种呢?
复习巩固
A
O
D
C
B
4
2
3
1
两线四角
O
A
B
C
D
)
(
1
3
4
2
)
(
邻补角(1):两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角.
如∠1与∠2有公共顶点O,有一条公共边OC,所以∠1和
∠2是互为邻补角.
邻补角(2):邻补角也可以看成是一条直线与端点在一条直线上的一条射线组成的两个角。
如∠1与∠2
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
性质
邻补角互补
对顶角相等
相同点
都有一个公共顶点,它们都是成对出现的
不同点
对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个
1、请判断:下列的∠1与∠2是否是对顶角?
1
2
1
2
1
2
1
2
1
2
1
2
1
1
2
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(若∠1=
∠2)
(若∠1=
∠2)
(若∠1=
∠2)
例题
2:如图,三条直线相交于一点O,说出图中所有对顶角。
A
B
C
D
E
F
O
E
A
B
C
D
O
C
D
F
O
A
B
E
F
O
复习巩固
A
B
C
D
o
直线
AB
与直线CD
互相垂直.
=
90°时,
符号:AB⊥CD,
垂足为o.
1、两条直线相交的特殊情形是?
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线,即:
垂线的性质1:
过一点有且只有一条直线与已知直线垂直.
连接直线外一点与直线上各点的所有连线中,垂线段最短。
垂线的性质2:
垂线段最短
点到直线的距离:垂线段的长度
1、
过点
P
向线段
AB
所在直线引垂线,正确的是(
).
A
B
C
D
C
例题
2、
过点P作线段或射线所在直线的垂线
A
B
.
.
.P
(1)
.
O
.P
.A
(2)
A
C
E
B
D
O
1
∴
∠EOB=90°(垂直的定义)
∴
∠
EOD=
∠
EOB+
∠
BOD
=90
°+55
°=145
°
(
解:
∵
AB⊥OE
(已知)
∵
∠BOD=
∠1=55°
3、
如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
(对顶角相等)
复习巩固
角的名称
位置特征
基本图形
图形结构特征
同位角
在两条被截直线的______
在截线的______
形如字母___
在两条被截直线的______
在截线的______
形如字母___
在两条被截直线的______
在截线的_____
形如字母___
“F”
同旁
同侧
内错角
之间
两侧
“Z”
同旁内角
之间
同侧
“U”
a
7
8
5
3
2
6
4
1
c
b
1、找出图中的同位角、内错角
、同旁内角:
例题
复习巩固
1、平行线的概念
2、平行公理
3、平行公理的推广
在同一平面内,永不相交的两条直线叫做平行线
在同一平面内过直线外一点,有且只有一条直线与已知直线平行
如果两条直线都与第三条直线平行,那么这两条直线与互相平行。
复习巩固
1、平行线的判定
2、平行线的性质
1、同位角相等,两直线平行
2、内错角相等,两直线平行
3、同旁内角互补,两直线平行
1、两直线平行,同位角相等
2、两直线平行,内错角相等
3、两直线平行,同旁内角互补
例题
1、如图,AB∥CD,∠B=35°,
∠1=75°.求∠A的度数.
解:
因为AB∥CD,∠B=35°,
所以∠2
=
∠B=35°,
∠ACD
=
∠1+
∠2
=
35°+
75°=
110°.
又因为AB∥CD,所以∠A+
∠
ACD=
180°,
所以∠A=
180°-
∠
ACD=
70°.
2、如图所示,∠1=∠2,∠3=110°,求∠4.
解:
因为∠1=∠2,
所以a//b
(内错角相等,两直线平行),
所以∠3=∠4
(两直线平行,同位角相等).
又因为∠3=
110°,
3、如图,∠BHE与∠BGF互为补角,∠D=∠A.求证:∠B=∠C.
解:
∵∠BHE+
∠BGF=180°,
∴∠BGF=
∠BHA(同角的补角相等),
∴AE//DF(同位角相等,两直线平行),
∠BHE+
∠BHA=180°,
∴∠A=
∠BFD(两直线平行,同位角相等).
∵∠D=∠A,所以∠BFD=
∠D,
∴AB//CD(内错角相等,两直线平行).
∴∠B=∠C(两直线平行,内错角相等).
⌒
⌒
A
B
C
D
E
60°
32°
1
2
F
解:过E作EF//AB
因为AB//CD
所以EF//CD
所以∠1=∠B=60°
所以∠2=∠D=32°
所以∠BED=∠1+
∠2
=60°+
32°=
92°
4、
已知:如图AB∥CD,
∠ABE=
60°,
∠CDE=
32°,求∠BED的度数.
解:因为CE⊥AB,
DF⊥AB
所以DF//EC
所以∠BDF=∠1,
∠EDF=∠3
因为ED//AC,
所以∠3=∠2
所以∠EDF=∠2
又CE平分∠ACB
所以∠1=∠2
所以∠BDF=∠EDF
1
3
2
5、如图,在?ABC中,CE⊥AB于点E,DF⊥AB于点F,AC//ED,CE是∠ACB的平分线,则∠EDF=∠BDF,请说明理由。
书山有路勤为径
学海无涯苦做舟
