苏科版七年级数学下册第9章整式乘法与因式分解压轴题强化训练(特优生提优)(Word版,附答案)
文档属性
| 名称 | 苏科版七年级数学下册第9章整式乘法与因式分解压轴题强化训练(特优生提优)(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 178.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 16:59:11 | ||
图片预览



文档简介
2021年苏科版七年级下册第九章压轴题题强化训练(特优生提优)
一、单选题
1.如果一个正整数可以表示为两个连续奇数的立方差,则称这个正整数为“和谐数”.如:2=13﹣(﹣1)3,26=33﹣13,2和26均为和谐数.那么,不超过2019的正整数中,所有的“和谐数”之和为(
)
A.6858
B.6860
C.9260
D.9262
2.已知是自然数,且满足,则的取值不可能是( )
A.5
B.6
C.7
D.8
3.248﹣1能被60到70之间的某两个整数整除,则这两个数是( )
A.61和63
B.63和65
C.65和67
D.64和67
4.将多项式加上一个整式,使它成为完全平方式,则下列不满足条件的整式是(
)
A.
B.±4x
C.
D.
5.已知,,,则代数式的值为(
)
A.0
B.1
C.2
D.3
6.如果四个互不相同的正整数m,n,p,q满足(6-m)(6-n)(6-p)(6-q)=4,那么m+n+p+q=(??
)
A.24
B.25
C.26
D.28
7.若……,则A的值是
A.0
B.1
C.
D.
二、解答题
8.阅读理解:
若x满足,求的值.
解:设,,则,,
所以
解决问题
(1)若x满足,求的值;
(2)若x满足,求的值;
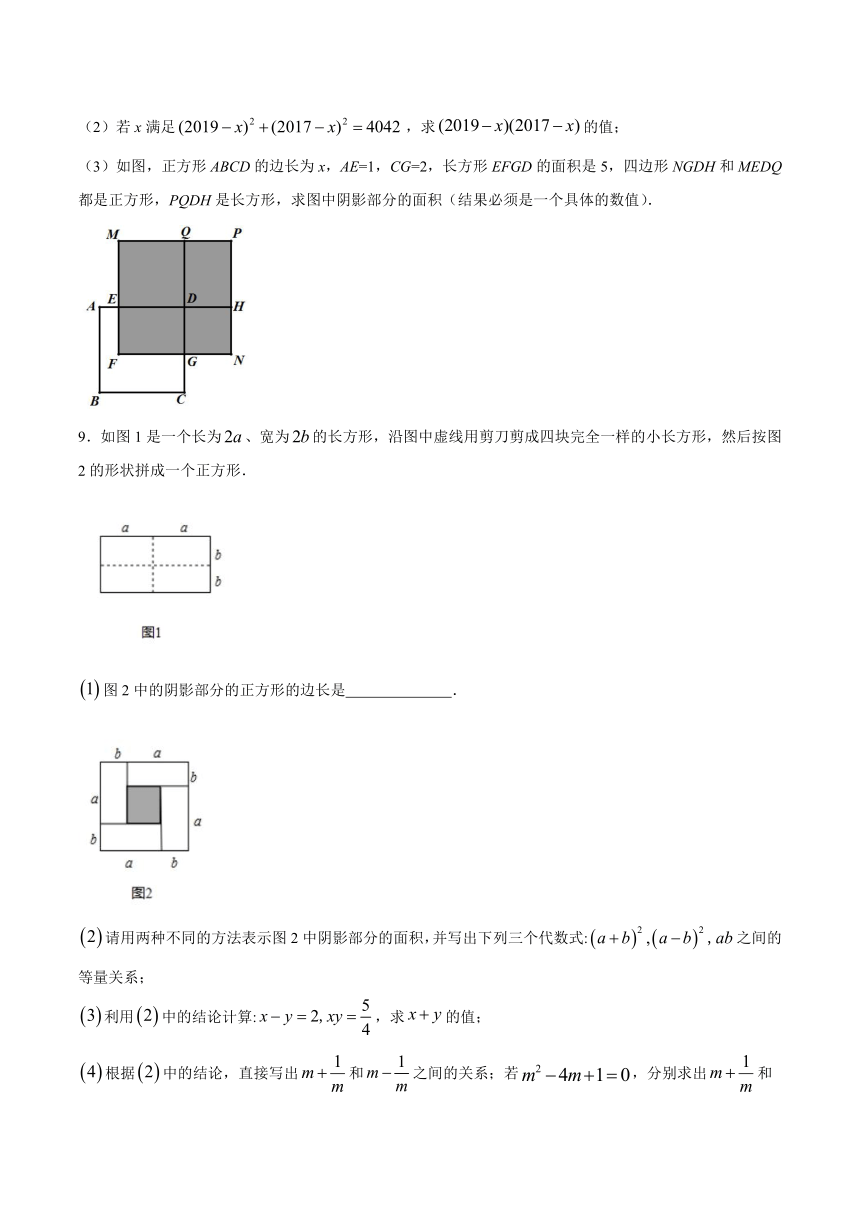
(3)如图,正方形ABCD的边长为x,AE=1,CG=2,长方形EFGD的面积是5,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
9.如图1是一个长为、宽为的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.
图2中的阴影部分的正方形的边长是
.
请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式:之间的等量关系;
利用中的结论计算:,求的值;
根据中的结论,直接写出和之间的关系;若,分别求出和的值.
10.你能化简(m﹣1)(m99+m98+…+m+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手,探究归纳出一些方法.
(1)分别化简下列各式:
(m﹣1)(m+1)=m2﹣1;
(m﹣1)(m2+m+1)=
;
(m﹣1)(m3+m2+m+1)=
;
(m﹣1)(mn+mn﹣1+mn﹣2+…+m+1)=
.
(2)请你利用上面的结论计算:299+298+297+…+2+1,写出计算过程.
(3)根据以上计算经验,直接写出3n+3n﹣1+3n﹣2+…+3+1结果
.
11.观察下列式子:
;
;
;
……
(1)上面的整式乘法计算结果比较简洁,类比学习过的平方差公式,完全平方公式的推导过程,请你写出一个新的乘法公式(用含a、b的字母表示),并加以证明;
(2)直接用你发现的公式写出计算结果:(2a+3b)(4a2﹣6ab+9b2)=
;
(3)分解因式:m3
+
n
3
+
3mn(m
+
n).
12.定义:对于依次排列的多项式x+a,x+b,x+c,x+d(a,b,c,d是常数),当它们满足在,且M为常数时,则称a,b,c,d是一组平衡数,M是该组平衡数的平衡因子,例如:对于多项式x+2,x+1,x+6,x+5,因为,所以2,1,6,5是一组平衡数,4是该组平衡数的平衡因子.
(1)已知2,4,7,9是一组平衡数,求该组平衡数的平衡因子M;
(2)若a,b,c,d是一组平衡数,a=-4,d=3,请直接写出组b,c的值;
(3)当a,b,c,d之间满是什么数量关系时,它们是一组平衡数,并说明理由.
13.分解因式:.
14.设,,,都是正整数,并且,,,求的值.
15.分解因式:.
16.分解因式:.
17.(1)填空:
;
;=
.
(2)猜想:
(a﹣b)(an﹣1+an﹣2b+…+abn﹣2+bn﹣1)=
(其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:的值.
18.阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知x2+2xy+2y2+2y+1=0,求2x+y的值;
(2)已知a﹣b=4,ab+c2﹣6c+13=0,求a+b+c的值.
19.已知:x2+xy+y=14,y2+xy+x=28,求x+y的值.
20.已知α+β=1,αβ=﹣1.设S1=α+β,S2=α2+β2,S3=α3+β3,…,Sn=αn+βn,
(1)计算:S1=
,S2=
,S3=
,S4=
;
(2)试写出Sn﹣2、Sn﹣1、Sn三者之间的关系;
(3)根据以上得出结论计算:α7+β7.
21.若正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k为“言唯一数”,交换其首位与个位的数字得到一个新数k',并记F(k)=.
(1)最大的四位“言唯一数”是
,最小的三位“言唯一数”是
;
(2)证明:对于任意的四位“言唯一数”m,m+m'能被11整除;
(3)设四位“言唯一数”n=1000x+100y+10y+1(2≤x≤9,0≤y≤9且y≠1,x、y均为整数),若F(n)仍然为“言唯一数”,求所有满足条件的四位“言唯一数”n.
22.已知正整数,,满足,,求的最大值.
三、填空题
23.若a-b=1,则的值为____________.
24.“元旦”期间小明去永辉超市购物,恰逢永辉超市“满1400减99元”促销活动,小明准备提前购置一些年货和,已知和的单价总和是100到200之间的整数,小明粗略测算了一下发现自己所购年货总价为1305元,不能达到超市的促销活动金额.
于是小明又购买了
、各一件,这样就能参加超市的促销活动,最后刚好付款1305元.
小明经仔细计算发现前面粗略测算时把
和的单价看反了,那么小明实际总共买了______件年货.
25.已知a1?a2?a3?…?a2007是彼此互不相等的负数,且M=(a1+a2+…+a2006)(a2+a3+…+a2007),N=(a1+a2+…+a2007)(a2+a3+…+a2006),那么M与N的大小关系是M___N.
26.已知,,,满足,,则__________.
27.若,则
________________.
28.已知a+b=8,ab=c2+16,则a+2b+3c的值为_____.
参考答案
1.B
2.D
3.B
4.D
5.D
6.A
7.D
8.(1)120;(2)2019;(3)21.
9.(1)
;(2)
;(3)
;(4)4,12
10.(1)m3﹣1;m4﹣1;mn+1﹣1;(2),计算过程略;(3).
11.(1)略;(2);(3)
12.(1)M=10;(2)b=
-3,c=2;(3)略.
13.
14.757.
15.
16.
17.(1)a2-b2,a3-b3,a4-b4(2)an-bn(3)311-211
18.(1)1;(2)3.
19.-7或6
20.(1)1,3,4,7;(2)Sn=Sn﹣1+Sn﹣2;(3)29.
21.(1)9991;221;(2)略;(3)满足条件的所有的四位“言唯一数”为和
22.2013.
23.1
24.22
25.M>N
26.60
27.8
28.12
一、单选题
1.如果一个正整数可以表示为两个连续奇数的立方差,则称这个正整数为“和谐数”.如:2=13﹣(﹣1)3,26=33﹣13,2和26均为和谐数.那么,不超过2019的正整数中,所有的“和谐数”之和为(
)
A.6858
B.6860
C.9260
D.9262
2.已知是自然数,且满足,则的取值不可能是( )
A.5
B.6
C.7
D.8
3.248﹣1能被60到70之间的某两个整数整除,则这两个数是( )
A.61和63
B.63和65
C.65和67
D.64和67
4.将多项式加上一个整式,使它成为完全平方式,则下列不满足条件的整式是(
)
A.
B.±4x
C.
D.
5.已知,,,则代数式的值为(
)
A.0
B.1
C.2
D.3
6.如果四个互不相同的正整数m,n,p,q满足(6-m)(6-n)(6-p)(6-q)=4,那么m+n+p+q=(??
)
A.24
B.25
C.26
D.28
7.若……,则A的值是
A.0
B.1
C.
D.
二、解答题
8.阅读理解:
若x满足,求的值.
解:设,,则,,
所以
解决问题
(1)若x满足,求的值;
(2)若x满足,求的值;
(3)如图,正方形ABCD的边长为x,AE=1,CG=2,长方形EFGD的面积是5,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
9.如图1是一个长为、宽为的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.
图2中的阴影部分的正方形的边长是
.
请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式:之间的等量关系;
利用中的结论计算:,求的值;
根据中的结论,直接写出和之间的关系;若,分别求出和的值.
10.你能化简(m﹣1)(m99+m98+…+m+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手,探究归纳出一些方法.
(1)分别化简下列各式:
(m﹣1)(m+1)=m2﹣1;
(m﹣1)(m2+m+1)=
;
(m﹣1)(m3+m2+m+1)=
;
(m﹣1)(mn+mn﹣1+mn﹣2+…+m+1)=
.
(2)请你利用上面的结论计算:299+298+297+…+2+1,写出计算过程.
(3)根据以上计算经验,直接写出3n+3n﹣1+3n﹣2+…+3+1结果
.
11.观察下列式子:
;
;
;
……
(1)上面的整式乘法计算结果比较简洁,类比学习过的平方差公式,完全平方公式的推导过程,请你写出一个新的乘法公式(用含a、b的字母表示),并加以证明;
(2)直接用你发现的公式写出计算结果:(2a+3b)(4a2﹣6ab+9b2)=
;
(3)分解因式:m3
+
n
3
+
3mn(m
+
n).
12.定义:对于依次排列的多项式x+a,x+b,x+c,x+d(a,b,c,d是常数),当它们满足在,且M为常数时,则称a,b,c,d是一组平衡数,M是该组平衡数的平衡因子,例如:对于多项式x+2,x+1,x+6,x+5,因为,所以2,1,6,5是一组平衡数,4是该组平衡数的平衡因子.
(1)已知2,4,7,9是一组平衡数,求该组平衡数的平衡因子M;
(2)若a,b,c,d是一组平衡数,a=-4,d=3,请直接写出组b,c的值;
(3)当a,b,c,d之间满是什么数量关系时,它们是一组平衡数,并说明理由.
13.分解因式:.
14.设,,,都是正整数,并且,,,求的值.
15.分解因式:.
16.分解因式:.
17.(1)填空:
;
;=
.
(2)猜想:
(a﹣b)(an﹣1+an﹣2b+…+abn﹣2+bn﹣1)=
(其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:的值.
18.阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)已知x2+2xy+2y2+2y+1=0,求2x+y的值;
(2)已知a﹣b=4,ab+c2﹣6c+13=0,求a+b+c的值.
19.已知:x2+xy+y=14,y2+xy+x=28,求x+y的值.
20.已知α+β=1,αβ=﹣1.设S1=α+β,S2=α2+β2,S3=α3+β3,…,Sn=αn+βn,
(1)计算:S1=
,S2=
,S3=
,S4=
;
(2)试写出Sn﹣2、Sn﹣1、Sn三者之间的关系;
(3)根据以上得出结论计算:α7+β7.
21.若正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k为“言唯一数”,交换其首位与个位的数字得到一个新数k',并记F(k)=.
(1)最大的四位“言唯一数”是
,最小的三位“言唯一数”是
;
(2)证明:对于任意的四位“言唯一数”m,m+m'能被11整除;
(3)设四位“言唯一数”n=1000x+100y+10y+1(2≤x≤9,0≤y≤9且y≠1,x、y均为整数),若F(n)仍然为“言唯一数”,求所有满足条件的四位“言唯一数”n.
22.已知正整数,,满足,,求的最大值.
三、填空题
23.若a-b=1,则的值为____________.
24.“元旦”期间小明去永辉超市购物,恰逢永辉超市“满1400减99元”促销活动,小明准备提前购置一些年货和,已知和的单价总和是100到200之间的整数,小明粗略测算了一下发现自己所购年货总价为1305元,不能达到超市的促销活动金额.
于是小明又购买了
、各一件,这样就能参加超市的促销活动,最后刚好付款1305元.
小明经仔细计算发现前面粗略测算时把
和的单价看反了,那么小明实际总共买了______件年货.
25.已知a1?a2?a3?…?a2007是彼此互不相等的负数,且M=(a1+a2+…+a2006)(a2+a3+…+a2007),N=(a1+a2+…+a2007)(a2+a3+…+a2006),那么M与N的大小关系是M___N.
26.已知,,,满足,,则__________.
27.若,则
________________.
28.已知a+b=8,ab=c2+16,则a+2b+3c的值为_____.
参考答案
1.B
2.D
3.B
4.D
5.D
6.A
7.D
8.(1)120;(2)2019;(3)21.
9.(1)
;(2)
;(3)
;(4)4,12
10.(1)m3﹣1;m4﹣1;mn+1﹣1;(2),计算过程略;(3).
11.(1)略;(2);(3)
12.(1)M=10;(2)b=
-3,c=2;(3)略.
13.
14.757.
15.
16.
17.(1)a2-b2,a3-b3,a4-b4(2)an-bn(3)311-211
18.(1)1;(2)3.
19.-7或6
20.(1)1,3,4,7;(2)Sn=Sn﹣1+Sn﹣2;(3)29.
21.(1)9991;221;(2)略;(3)满足条件的所有的四位“言唯一数”为和
22.2013.
23.1
24.22
25.M>N
26.60
27.8
28.12
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
