福建省福州八县(市)一中11-12学年高一上学期期末联考试卷数学
文档属性
| 名称 | 福建省福州八县(市)一中11-12学年高一上学期期末联考试卷数学 |
|
|
| 格式 | zip | ||
| 文件大小 | 376.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-28 00:00:00 | ||
图片预览





文档简介
2011-----2012学年度第一学期八县(市)一中期末联考
高一数学
考试日期: 1月 10日 完卷时间: 120 分钟 满 分: 150 分
说明:1.答卷前,考生必须将自己的姓名、座号、班级、准考证号码等按要求填写。
2.请将所有题的答案写在指定的答题卷上,考试结束时只交答题卷。
参考公式:
锥体体积(其中是底面积,是高),球体体积(其中是半径)。
一.选择题(本大题共12小题,每小题5分,共60分。每题只有一个正确答案)
1.“点M在直线a上,a 在平面内”可表示为( )
A. B. C. D.
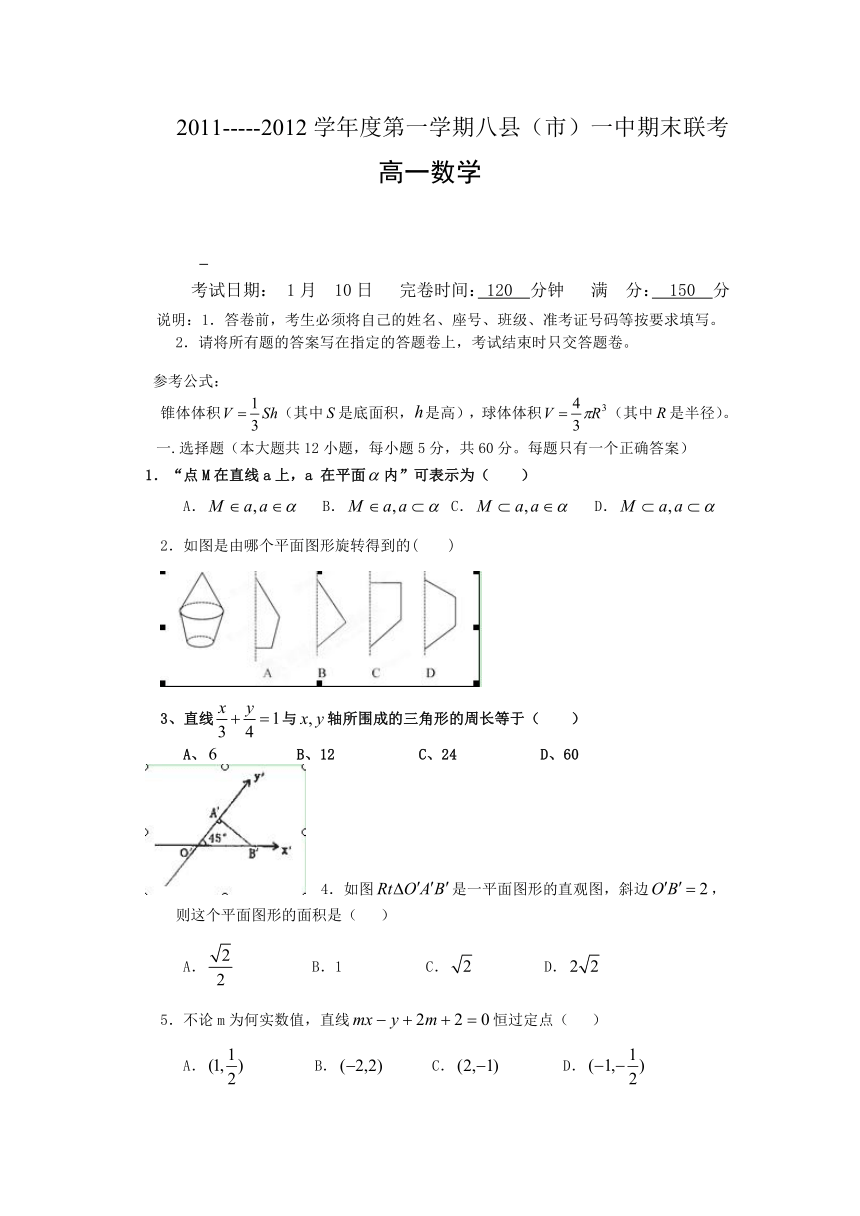
2.如图是由哪个平面图形旋转得到的( )
3、直线与轴所围成的三角形的周长等于( )
A、 B、12 C、24 D、60
4.如图是一平面图形的直观图,斜边,
则这个平面图形的面积是( )
A. B.1 C. D.
5.不论m为何实数值,直线恒过定点( )
A. B. C. D.
6.在空间四边形ABCD各边AB、BC、CD、DA上分别取E、F、G、H四点,
如果与EF、GH能相交于点P,那么 ( )
A、点必P在直线AC上 B、点P必在直线BD上
C、点P必在平面ABC内 D、点P必在平面ABC外
7.如果直线与直线互相垂直,则实数a的值等于( )
A.1 B.-2 C. D.
8.设是两条不同的直线,是三个不同的平面,给出下列四个命题:
①若;②;
③;④,其中正确命题的序号是( )
A、①和② B、②和③ C、③和④ D、①和④
9. 已知直线和互相平行,则它们之间的距离是( )
A. B. C. D.
10.如图,是⊙0直径,是圆周上不同于的任意一点,
平面,则四面体的四个面中,直角三角形的个数有( )
A、个 B、个 C、个 D、个
11. 入射光线线在直线:上,经过轴反射到直线上,再经过
轴反射到直线上,则直线的方程为( )
A. B.
C. D.
12.如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是
A. AC⊥SB B. AB∥平面SCD
C. SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
二、填空题(本大题共4小题,每小题4分,共16分)
13. 点到直线的距离为_______.
14.已知某几何体的三视图如右图所示,则该几何体的体积为
15.与直线2x+3y+5=0平行,且在两坐标轴上截距的和为6的直线方程是 .
16. 将边长为的正方形沿对角线折起,使得平面平面,在折起后形成的三棱锥中,给出下列三个命题:
①面是等边三角形; ②;
③三棱锥的体积是.
其中正确命题的序号是_ .(写出所有正确命题的序号)
三.解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
如图,在正方体中,
(Ⅰ) 求证:;
(Ⅱ) 求二面角的正切值.
18、(本小题满分12分)如图,在平行四边形中,边所在直线方程为,
点。
(1)求直线的方程;(2)求边上的高所在直线的方程。
19.(本小题满分12分)已知ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F是侧棱PD、PC的中点。
(1)求证:平面PAB ;
(2)求直线PC与底面ABCD所成角的正切值。
20.已知点,,,,点在线段CD垂直平分线上,
求(1)线段CD垂直平分线方程。(2)取得最小值时点的坐标。
21. (本小题满分12分)如图,在四棱锥中,是正方形,平面,, 分别是的中点.
(1)求四棱锥P-ABCD的体积
(2)求证:平面平面;
(3)在线段上确定一点,使平面,并给出证明;
22、(本小题满分14分)如图,在直角坐标系中,射线:,:,
过点作直线分别交射线、于、点.
(1)当的中点为时,求直线的方程;
(2)当的中点在直线上时,求直线的方程.
2011---2012学年度第一学期八县(市)一中期末联考
高中 一 年 数学 科试卷参考答案
一、选择题:(每小题 5 分,共 60 分)
三.解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
如图,在正方体中,
(Ⅰ) 求证:;
(Ⅱ) 求二面角的正切值.
17.(Ⅰ)证明:由正方体得:
,且
(写成,且不扣分)
∴ 四边形BB1D1D是平行四边形
∴ …………………………………………………………4分
.又∵ 平面,平面
∴ 平面……………………………………………………………6分
18、(本小题满分12分)如图,在平行四边形中,边所在直线方程为,点。
(1)求直线的方程;(2)求边上的高所在直线的方程。
19.(本小题满分12分)已知ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F是侧棱PD、PC的中点。
(1)求证:平面PAB ;
(2)求直线PC与底面ABCD所成角的正切值。
证明:(2)连结AC,因为PA平面ABCD,所以就为直线PC与平面ABCD所成的角。即
又因为正方形ABCD的边长为2,所以AC=,
所以………………………………12分
21. (本小题满分12分)如图,在四棱锥中,是正方形,平面,, 分别是的中点.
(1)求四棱锥P-ABCD的体积
(2)求证:平面平面;
(3)在线段上确定一点,使平面,并给出证明;
22、如图,在直角坐标系中,射线:,:,
过点作直线分别交射线、于、点.
(1)当的中点为时,求直线的方程;
(2)当的中点在直线上时,求直线的方程.
则两点的坐标分别为,.-------(10分)
∴的中点坐标为, -------(11分)
又的中点在直线上, ∴=,
解之得:. -------(13分)
∴的方程为,即. ------(14分)
A
B
D
E
F
P
G
C
高一数学
考试日期: 1月 10日 完卷时间: 120 分钟 满 分: 150 分
说明:1.答卷前,考生必须将自己的姓名、座号、班级、准考证号码等按要求填写。
2.请将所有题的答案写在指定的答题卷上,考试结束时只交答题卷。
参考公式:
锥体体积(其中是底面积,是高),球体体积(其中是半径)。
一.选择题(本大题共12小题,每小题5分,共60分。每题只有一个正确答案)
1.“点M在直线a上,a 在平面内”可表示为( )
A. B. C. D.
2.如图是由哪个平面图形旋转得到的( )
3、直线与轴所围成的三角形的周长等于( )
A、 B、12 C、24 D、60
4.如图是一平面图形的直观图,斜边,
则这个平面图形的面积是( )
A. B.1 C. D.
5.不论m为何实数值,直线恒过定点( )
A. B. C. D.
6.在空间四边形ABCD各边AB、BC、CD、DA上分别取E、F、G、H四点,
如果与EF、GH能相交于点P,那么 ( )
A、点必P在直线AC上 B、点P必在直线BD上
C、点P必在平面ABC内 D、点P必在平面ABC外
7.如果直线与直线互相垂直,则实数a的值等于( )
A.1 B.-2 C. D.
8.设是两条不同的直线,是三个不同的平面,给出下列四个命题:
①若;②;
③;④,其中正确命题的序号是( )
A、①和② B、②和③ C、③和④ D、①和④
9. 已知直线和互相平行,则它们之间的距离是( )
A. B. C. D.
10.如图,是⊙0直径,是圆周上不同于的任意一点,
平面,则四面体的四个面中,直角三角形的个数有( )
A、个 B、个 C、个 D、个
11. 入射光线线在直线:上,经过轴反射到直线上,再经过
轴反射到直线上,则直线的方程为( )
A. B.
C. D.
12.如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是
A. AC⊥SB B. AB∥平面SCD
C. SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
二、填空题(本大题共4小题,每小题4分,共16分)
13. 点到直线的距离为_______.
14.已知某几何体的三视图如右图所示,则该几何体的体积为
15.与直线2x+3y+5=0平行,且在两坐标轴上截距的和为6的直线方程是 .
16. 将边长为的正方形沿对角线折起,使得平面平面,在折起后形成的三棱锥中,给出下列三个命题:
①面是等边三角形; ②;
③三棱锥的体积是.
其中正确命题的序号是_ .(写出所有正确命题的序号)
三.解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
如图,在正方体中,
(Ⅰ) 求证:;
(Ⅱ) 求二面角的正切值.
18、(本小题满分12分)如图,在平行四边形中,边所在直线方程为,
点。
(1)求直线的方程;(2)求边上的高所在直线的方程。
19.(本小题满分12分)已知ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F是侧棱PD、PC的中点。
(1)求证:平面PAB ;
(2)求直线PC与底面ABCD所成角的正切值。
20.已知点,,,,点在线段CD垂直平分线上,
求(1)线段CD垂直平分线方程。(2)取得最小值时点的坐标。
21. (本小题满分12分)如图,在四棱锥中,是正方形,平面,, 分别是的中点.
(1)求四棱锥P-ABCD的体积
(2)求证:平面平面;
(3)在线段上确定一点,使平面,并给出证明;
22、(本小题满分14分)如图,在直角坐标系中,射线:,:,
过点作直线分别交射线、于、点.
(1)当的中点为时,求直线的方程;
(2)当的中点在直线上时,求直线的方程.
2011---2012学年度第一学期八县(市)一中期末联考
高中 一 年 数学 科试卷参考答案
一、选择题:(每小题 5 分,共 60 分)
三.解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
如图,在正方体中,
(Ⅰ) 求证:;
(Ⅱ) 求二面角的正切值.
17.(Ⅰ)证明:由正方体得:
,且
(写成,且不扣分)
∴ 四边形BB1D1D是平行四边形
∴ …………………………………………………………4分
.又∵ 平面,平面
∴ 平面……………………………………………………………6分
18、(本小题满分12分)如图,在平行四边形中,边所在直线方程为,点。
(1)求直线的方程;(2)求边上的高所在直线的方程。
19.(本小题满分12分)已知ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F是侧棱PD、PC的中点。
(1)求证:平面PAB ;
(2)求直线PC与底面ABCD所成角的正切值。
证明:(2)连结AC,因为PA平面ABCD,所以就为直线PC与平面ABCD所成的角。即
又因为正方形ABCD的边长为2,所以AC=,
所以………………………………12分
21. (本小题满分12分)如图,在四棱锥中,是正方形,平面,, 分别是的中点.
(1)求四棱锥P-ABCD的体积
(2)求证:平面平面;
(3)在线段上确定一点,使平面,并给出证明;
22、如图,在直角坐标系中,射线:,:,
过点作直线分别交射线、于、点.
(1)当的中点为时,求直线的方程;
(2)当的中点在直线上时,求直线的方程.
则两点的坐标分别为,.-------(10分)
∴的中点坐标为, -------(11分)
又的中点在直线上, ∴=,
解之得:. -------(13分)
∴的方程为,即. ------(14分)
A
B
D
E
F
P
G
C
同课章节目录
