16.3.2《分式方程的应用》
文档属性
| 名称 | 16.3.2《分式方程的应用》 |  | |
| 格式 | zip | ||
| 文件大小 | 193.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-28 17:10:37 | ||
图片预览








文档简介
(共21张PPT)
第二课时 分式方程的应用
列一元一次方程解应用题的一般步骤:
学 前 温 故
(1)审:审题,分析题中已知什么,求什么,明确各数量之间的关系;
(2)设:设未知数,用字母表示其他未知数;
(3)找:找出能够表示应用题全部意义的一个________;
(4)列:根据题中的相等关系列出____;
(5)解:解方程,求出未知数的值;
(6)答:检验所得解是否符合题意,写出问题的答案.
相等关系
方程
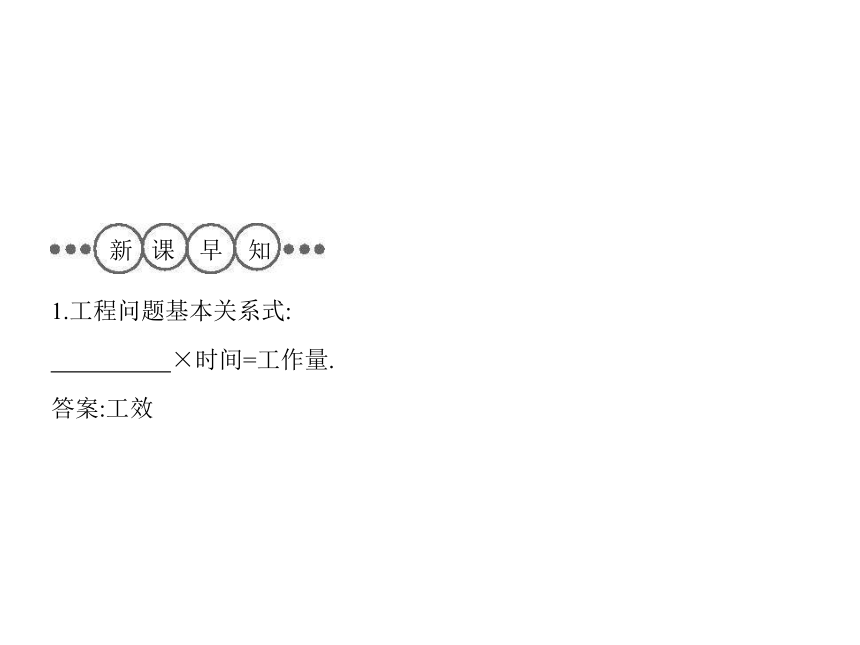
1.工程问题基本关系式:
×时间=工作量.
答案:工效
新 课 早 知
2.某施工队挖掘一条长96 m的隧道,开工后每天比原计划多挖2 m,结果提 前4天完成任务,原计划每天挖多少米 若设原计划每天挖x m,则依题意列 出正确的方程为( ).
A. - =4 B. - =4
C. - =4 D. - =4
答案:C
3.行程问题基本关系式:
速度×时间= .
答案:路程
知水流速度为3千米/时,设轮船在静水中的速度为x千米/时,可列方程为 .
答案: =
4.轮船顺水航行40千米所需的时间和逆水航行30千米所需的时间相同.已
5.列分式方程解应用题的基本步骤:
(1) ——仔细审题,找出等量关系;
(2) ——合理设未知数;
(3) ——根据等量关系列出方程(组);
(4) ——解出方程(组);
(5) ——检验;
(6) ——答题.
答案:(1)审 (2)设 (3)列 (4)解 (5)验 (6)答
6.小兰的妈妈在供销大厦用12.50元买了若干瓶酸奶,但她在百货商场食品 自选室内发现,同样的酸奶,这里要比供销大厦每瓶便宜0.2元钱,因此,当第 二次买酸奶时,便到百货商场去买,结果用去18.40元钱,买的瓶数比第一次 的瓶数多 倍,问她第一次在供销大厦买了几瓶
分析:等量关系为:酸奶的单价×瓶数=购买酸奶的总钱数;若设第一次在供 销大厦买了x瓶酸奶,那么相等关系有:供销大厦酸奶单价-百货商场酸奶单 价=0.2元钱.
解:设她第一次在供销大厦买了x瓶酸奶,
由题意,得 - =0.2,
解之,得x=5.
经检验,x=5是原方程的根且符合题意.
答:她第一次在供销大厦买了5瓶酸奶.
1.列分式方程解工程问题应用题
【例1】 在社会主义新农村建设中,某乡镇决定对一段公路进行改造.已知 这项工程中甲工程队单独做需要40天完成,如果由乙工程队先单独做10天, 那么剩下的工程还需要两队合作20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)求两队合作完成这项工程所需的天数.
解:(1)设乙工程队单独完成这项工程需要x天,根据题意得 + ×20=
1,
解之,得x=60,经检验,x=60是原方程的解.
答:乙工程队单独完成这项工程需要60天.
(2)设两队合作完成这项工程所需的天数为y,根据题意得 y=1,解
之,得y=24.
答:两队合作完成这项工程需要24天.
点拨:列方程解应用题的关键在审题,审题时,首先要知道问题中涉及哪些 量,这些量中哪些是已知量,哪些是未知量,并找出相关量间的相等关系,再
设未知数,利用相等关系列出方程或方程组.
2.列分式方程解行程问题应用题
【例2】 一小船由A港到B港顺流需行6小时,由B港到A港逆流需行8小时. 一天,小船早晨6点由A港出发顺流行至B港时,发现一救生圈在途中掉落在 水中,立即返回,1小时后找到救生圈.问:
(1)若小船按水流速度由A港漂流到B港要多少小时
(2)救生圈是何时掉入水中的
解:(1)设小船由A港漂流到B港用x小时,则水速为 ,由静水速度=顺流速度-
水速=逆流速度+水速,列方程 - = + ,
解这个方程,得x=48.
经检验,x=48是原方程的根.
答:小船按水流速度由A港漂流到B港要48小时.
(2)设救生圈在y点钟落入水中,由问题(1)可知水流速度为每小时 ,小船顺
流由A港到B港用6小时,逆流走1小时,同时救生圈又顺流向前漂了1小时,依 题意,有(12-y)· = ×1,
解得y=11.
答:救生圈在中午11点落水.
点拨:此题属于行程问题中顺水、逆水问题.顺水速度、逆水速度、与船在 静水中速度和水流速度的关系为:静水速度=顺水速度-水流速度=逆水速度 +水流速度.
1.某校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结 果比用原价多买了20瓶,求原价每瓶多少元 设原价每瓶x元,则可列出方程 为( ).
A. - =20 B. - =20
C. - =0.5 D. - =0.5
解析:设原价每瓶x元,能买 瓶,现价每瓶(x-0.5)元,能买 瓶,这样现在
比原先多买20瓶,所以列方程为 - =20,故选B.
答案:B
2.甲、乙分别从相距36千米的A,B两地同时相向而行.甲从A出发1千米后发 现有东西遗忘在A地,立即返回,取过东西后又立即从A向B行进,这样二人恰 好在AB中点处相遇,又知甲比乙每小时多走0.5千米,求二人的速度.
解:设乙的速度为x千米/时,则甲的速度为 千米/时.
根据题意,得 = ,解得x=4.5.
经检验,x=4.5是方程的解.
当x=4.5时,x+ =5.
答:甲的速度为5千米/时,乙的速度为4.5千米/时.
3.到2011年1月山东省气象干旱程度已达特大干旱等级,有32万人发生临时 性饮水困难,旱情牵动着全国人民的心.“一方有难、八方支援”,某厂计 划生产1 800吨纯净水支援灾区人民,为尽快把纯净水发往灾区,工人把每 天的工作效率提高到原计划的1.5倍,结果比原计划提前3天完成了生产任 务.求原计划每天生产多少吨纯净水
解:设原计划每天生产x吨纯净水,
则依据题意,得 - =3,
整理,得4.5x=900,解之,得x=200,
把x代入原方程,成立,
∴x=200是原方程的解.
答:原计划每天生产200吨纯净水.
第二课时 分式方程的应用
列一元一次方程解应用题的一般步骤:
学 前 温 故
(1)审:审题,分析题中已知什么,求什么,明确各数量之间的关系;
(2)设:设未知数,用字母表示其他未知数;
(3)找:找出能够表示应用题全部意义的一个________;
(4)列:根据题中的相等关系列出____;
(5)解:解方程,求出未知数的值;
(6)答:检验所得解是否符合题意,写出问题的答案.
相等关系
方程
1.工程问题基本关系式:
×时间=工作量.
答案:工效
新 课 早 知
2.某施工队挖掘一条长96 m的隧道,开工后每天比原计划多挖2 m,结果提 前4天完成任务,原计划每天挖多少米 若设原计划每天挖x m,则依题意列 出正确的方程为( ).
A. - =4 B. - =4
C. - =4 D. - =4
答案:C
3.行程问题基本关系式:
速度×时间= .
答案:路程
知水流速度为3千米/时,设轮船在静水中的速度为x千米/时,可列方程为 .
答案: =
4.轮船顺水航行40千米所需的时间和逆水航行30千米所需的时间相同.已
5.列分式方程解应用题的基本步骤:
(1) ——仔细审题,找出等量关系;
(2) ——合理设未知数;
(3) ——根据等量关系列出方程(组);
(4) ——解出方程(组);
(5) ——检验;
(6) ——答题.
答案:(1)审 (2)设 (3)列 (4)解 (5)验 (6)答
6.小兰的妈妈在供销大厦用12.50元买了若干瓶酸奶,但她在百货商场食品 自选室内发现,同样的酸奶,这里要比供销大厦每瓶便宜0.2元钱,因此,当第 二次买酸奶时,便到百货商场去买,结果用去18.40元钱,买的瓶数比第一次 的瓶数多 倍,问她第一次在供销大厦买了几瓶
分析:等量关系为:酸奶的单价×瓶数=购买酸奶的总钱数;若设第一次在供 销大厦买了x瓶酸奶,那么相等关系有:供销大厦酸奶单价-百货商场酸奶单 价=0.2元钱.
解:设她第一次在供销大厦买了x瓶酸奶,
由题意,得 - =0.2,
解之,得x=5.
经检验,x=5是原方程的根且符合题意.
答:她第一次在供销大厦买了5瓶酸奶.
1.列分式方程解工程问题应用题
【例1】 在社会主义新农村建设中,某乡镇决定对一段公路进行改造.已知 这项工程中甲工程队单独做需要40天完成,如果由乙工程队先单独做10天, 那么剩下的工程还需要两队合作20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)求两队合作完成这项工程所需的天数.
解:(1)设乙工程队单独完成这项工程需要x天,根据题意得 + ×20=
1,
解之,得x=60,经检验,x=60是原方程的解.
答:乙工程队单独完成这项工程需要60天.
(2)设两队合作完成这项工程所需的天数为y,根据题意得 y=1,解
之,得y=24.
答:两队合作完成这项工程需要24天.
点拨:列方程解应用题的关键在审题,审题时,首先要知道问题中涉及哪些 量,这些量中哪些是已知量,哪些是未知量,并找出相关量间的相等关系,再
设未知数,利用相等关系列出方程或方程组.
2.列分式方程解行程问题应用题
【例2】 一小船由A港到B港顺流需行6小时,由B港到A港逆流需行8小时. 一天,小船早晨6点由A港出发顺流行至B港时,发现一救生圈在途中掉落在 水中,立即返回,1小时后找到救生圈.问:
(1)若小船按水流速度由A港漂流到B港要多少小时
(2)救生圈是何时掉入水中的
解:(1)设小船由A港漂流到B港用x小时,则水速为 ,由静水速度=顺流速度-
水速=逆流速度+水速,列方程 - = + ,
解这个方程,得x=48.
经检验,x=48是原方程的根.
答:小船按水流速度由A港漂流到B港要48小时.
(2)设救生圈在y点钟落入水中,由问题(1)可知水流速度为每小时 ,小船顺
流由A港到B港用6小时,逆流走1小时,同时救生圈又顺流向前漂了1小时,依 题意,有(12-y)· = ×1,
解得y=11.
答:救生圈在中午11点落水.
点拨:此题属于行程问题中顺水、逆水问题.顺水速度、逆水速度、与船在 静水中速度和水流速度的关系为:静水速度=顺水速度-水流速度=逆水速度 +水流速度.
1.某校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结 果比用原价多买了20瓶,求原价每瓶多少元 设原价每瓶x元,则可列出方程 为( ).
A. - =20 B. - =20
C. - =0.5 D. - =0.5
解析:设原价每瓶x元,能买 瓶,现价每瓶(x-0.5)元,能买 瓶,这样现在
比原先多买20瓶,所以列方程为 - =20,故选B.
答案:B
2.甲、乙分别从相距36千米的A,B两地同时相向而行.甲从A出发1千米后发 现有东西遗忘在A地,立即返回,取过东西后又立即从A向B行进,这样二人恰 好在AB中点处相遇,又知甲比乙每小时多走0.5千米,求二人的速度.
解:设乙的速度为x千米/时,则甲的速度为 千米/时.
根据题意,得 = ,解得x=4.5.
经检验,x=4.5是方程的解.
当x=4.5时,x+ =5.
答:甲的速度为5千米/时,乙的速度为4.5千米/时.
3.到2011年1月山东省气象干旱程度已达特大干旱等级,有32万人发生临时 性饮水困难,旱情牵动着全国人民的心.“一方有难、八方支援”,某厂计 划生产1 800吨纯净水支援灾区人民,为尽快把纯净水发往灾区,工人把每 天的工作效率提高到原计划的1.5倍,结果比原计划提前3天完成了生产任 务.求原计划每天生产多少吨纯净水
解:设原计划每天生产x吨纯净水,
则依据题意,得 - =3,
整理,得4.5x=900,解之,得x=200,
把x代入原方程,成立,
∴x=200是原方程的解.
答:原计划每天生产200吨纯净水.
