19.2.2《菱形》
图片预览






文档简介
(共27张PPT)
19.2.2 菱形
1.矩形的性质:(1)矩形的四个角都是____;(2)矩形的对角线____.
学 前 温 故
2.矩形的判定:(1)有一个角是直角的__________是矩形;(2)对角线_______的平行四边形是矩形.
直角
相等
平行四边形
相
等
1.菱形的概念
有一组邻边 的平行四边形叫做菱形.
答案:相等
新 课 早 知
2.菱形的性质
菱形的四条边都 ;菱形的两条对角线 ,并且每 一条对角线平分一组 .
答案:相等 互相垂直 对角
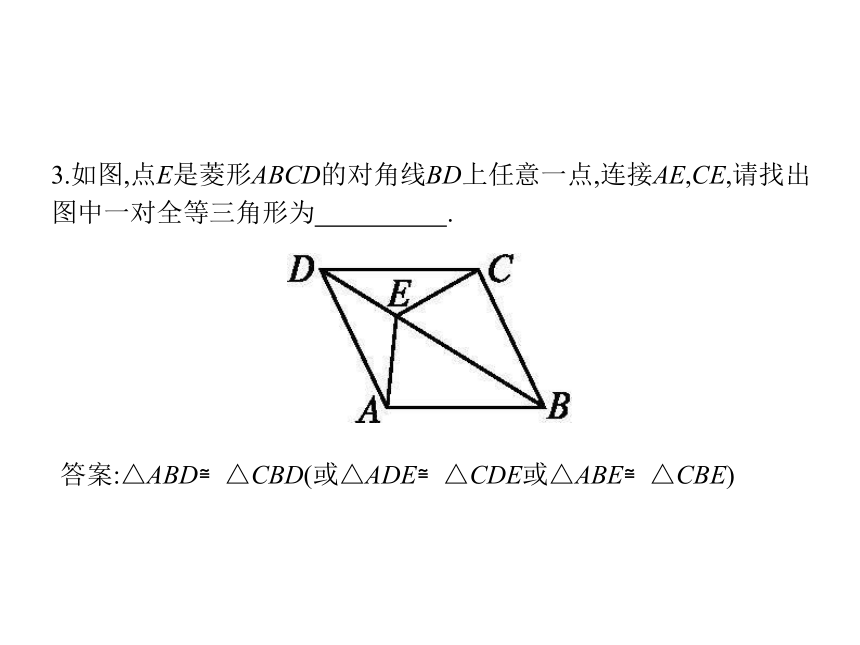
3.如图,点E是菱形ABCD的对角线BD上任意一点,连接AE,CE,请找出 图中一对全等三角形为 .
答案:△ABD≌△CBD(或△ADE≌△CDE或△ABE≌△CBE)
4.菱形的判定
(1)一组 相等的平行四边形是菱形.
(2)对角线 的平行四边形是菱形.
(3)四边 的四边形是菱形.
答案:(1)邻边 (2)互相垂直 (3)相等
5.下列说法错误的是( ).
A.一组邻边相等的四边形是菱形
B.对角线垂直的平行四边形是菱形
C.对角线互相平分且有一组邻边相等的四边形是菱形
D.四条边都相等的四边形是菱形
答案:A
6.菱形的面积等于对角线乘积的 .
答案:一半
7.一个菱形的对角线长分别是4 cm,5 cm,则这个菱形的面积S等于 .
答案:10 cm2
1.菱形的性质
【例1】 如图,菱形ABCD的边长为2,对角线BD=2,E,F分别是AD,CD 上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.同时指出△BCF是由△BDE经过 如何变换得到的
(1)证明:∵菱形ABCD的边长为2,BD=2,
∴BD=BC且∠BDE=∠BCF=60°.
∵AE+CF=2,又∵AE+DE=AD=2,
∴DE=CF.∴△BDE≌△BCF.
理由如下:由(1)得△BDE≌△BCF,
∴BE=BF,∠CBF=∠DBE.
∴∠EBF=∠EBD+∠DBF=∠CBF+∠DBF=60°.
∴△BEF是等边三角形,△BCF是由△BDE绕点B顺时针旋转60°得 到的.
点拨:由菱形的性质可知,菱形中存在很多线段的关系和角的关系,因 此,在解决有关菱形的问题时,经常转化为证两三角形全等或运用直 角三角形和等腰三角形的性质等来解决.
(2)解:△BEF是等边三角形,
2.菱形的判定
【例2】 如图所示, ABCD的对角线AC与BD相交于点O,且AC=4, BD=2 ,AB= .过点D作DE⊥AB,垂足为E.
(1)四边形ABCD是菱形吗 说说你的理由.
(2)求DE的长.
解:(1)四边形ABCD是菱形.理由如下:
∵ ABCD的对角线AC与BD互相平分,
∴OA= AC=2,OB= BD= .
∵22+( )2=7=( )2,AB2=OA2+OB2,
∴∠AOB=90°.∴AC⊥BD.
∴平行四边形ABCD是菱形.
(2)由AB·DE= AC·BD,得DE= = .
点拨:(1)菱形的判定方法有多种,在判定一个四边形是菱形时,要选 择简便方法.有时要先判定四边形是平行四边形,再判定为菱形.(2) 菱形的面积可由两种方法求得,①用求平行四边形面积的方法求解, ②用对角线乘积的一半求其面积.
1.下列命题中正确的是( ),
A.对角线相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形
D.对角线互相垂直的平行四边形是菱形
解析:选项A,B不能判定是菱形;选项C,对角线相等的平行四边形应 是矩形,所以C错误,故选D.
答案:D
2.(2011·江苏无锡中考)菱形具有而矩形不一定具有的性质是( ).
A.对角线互相垂直
B.对角线相等
C.对角线互相平分
D.对角互补
答案:A
3.如图所示,在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的边 长为( ).
A.5
B.6
C.8
D.10
解析:因为菱形的对角线互相垂直且平分,所以在Rt△AOB中,根据勾 股定理可得AB= = =5,即菱形的边长为5.
答案:A
4.如图,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周 长为( ).
A.20 B.18
C.16 D.15
解析:由题意可知,△ABC是等边三角形,
所以AB=BC=AC=4.
因为菱形的四条边都相等,故菱形ABCD的周长为16.
答案:C
5.(2011·广州中考)如图,AC是菱形ABCD的对角线,点E,F分别在边 AB,AD上,且AE=AF.
求证:△ACE≌△ACF.
证明:∵四边形ABCD为菱形,
∴∠BAC=∠DAC.
又∵AE=AF,AC=AC,
∴△ACE≌△ACF(SAS).
6.已知在菱形ABCD中,O是对角线BD上的一动点.如图,P为线段BC 上一点,连接PO,并延长交AD于点Q,当O是BD的中点时,求证:OP= OQ.
证明:∵四边形ABCD为菱形,∴AD∥BC.
∴∠OBP=∠ODQ.
∵O是BD的中点,∴OB=OD.
在△BOP和△DOQ中,
∵∠OBP=∠ODQ,OB=OD,∠BOP=∠DOQ,
∴△BOP≌△DOQ(ASA),∴OP=OQ.
7.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
解:(1)四边形OCED是菱形.理由如下:
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又在矩形ABCD中,OC=OD,
∴四边形OCED是菱形.
(2)连接OE,由菱形OCED得CD⊥OE,
∴OE∥BC.
又CE∥BD,∴四边形BCEO是平行四边形.
∴OE=BC=8,
∴S四边形OCED= OE·CD= ×8×6=24.
19.2.2 菱形
1.矩形的性质:(1)矩形的四个角都是____;(2)矩形的对角线____.
学 前 温 故
2.矩形的判定:(1)有一个角是直角的__________是矩形;(2)对角线_______的平行四边形是矩形.
直角
相等
平行四边形
相
等
1.菱形的概念
有一组邻边 的平行四边形叫做菱形.
答案:相等
新 课 早 知
2.菱形的性质
菱形的四条边都 ;菱形的两条对角线 ,并且每 一条对角线平分一组 .
答案:相等 互相垂直 对角
3.如图,点E是菱形ABCD的对角线BD上任意一点,连接AE,CE,请找出 图中一对全等三角形为 .
答案:△ABD≌△CBD(或△ADE≌△CDE或△ABE≌△CBE)
4.菱形的判定
(1)一组 相等的平行四边形是菱形.
(2)对角线 的平行四边形是菱形.
(3)四边 的四边形是菱形.
答案:(1)邻边 (2)互相垂直 (3)相等
5.下列说法错误的是( ).
A.一组邻边相等的四边形是菱形
B.对角线垂直的平行四边形是菱形
C.对角线互相平分且有一组邻边相等的四边形是菱形
D.四条边都相等的四边形是菱形
答案:A
6.菱形的面积等于对角线乘积的 .
答案:一半
7.一个菱形的对角线长分别是4 cm,5 cm,则这个菱形的面积S等于 .
答案:10 cm2
1.菱形的性质
【例1】 如图,菱形ABCD的边长为2,对角线BD=2,E,F分别是AD,CD 上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.同时指出△BCF是由△BDE经过 如何变换得到的
(1)证明:∵菱形ABCD的边长为2,BD=2,
∴BD=BC且∠BDE=∠BCF=60°.
∵AE+CF=2,又∵AE+DE=AD=2,
∴DE=CF.∴△BDE≌△BCF.
理由如下:由(1)得△BDE≌△BCF,
∴BE=BF,∠CBF=∠DBE.
∴∠EBF=∠EBD+∠DBF=∠CBF+∠DBF=60°.
∴△BEF是等边三角形,△BCF是由△BDE绕点B顺时针旋转60°得 到的.
点拨:由菱形的性质可知,菱形中存在很多线段的关系和角的关系,因 此,在解决有关菱形的问题时,经常转化为证两三角形全等或运用直 角三角形和等腰三角形的性质等来解决.
(2)解:△BEF是等边三角形,
2.菱形的判定
【例2】 如图所示, ABCD的对角线AC与BD相交于点O,且AC=4, BD=2 ,AB= .过点D作DE⊥AB,垂足为E.
(1)四边形ABCD是菱形吗 说说你的理由.
(2)求DE的长.
解:(1)四边形ABCD是菱形.理由如下:
∵ ABCD的对角线AC与BD互相平分,
∴OA= AC=2,OB= BD= .
∵22+( )2=7=( )2,AB2=OA2+OB2,
∴∠AOB=90°.∴AC⊥BD.
∴平行四边形ABCD是菱形.
(2)由AB·DE= AC·BD,得DE= = .
点拨:(1)菱形的判定方法有多种,在判定一个四边形是菱形时,要选 择简便方法.有时要先判定四边形是平行四边形,再判定为菱形.(2) 菱形的面积可由两种方法求得,①用求平行四边形面积的方法求解, ②用对角线乘积的一半求其面积.
1.下列命题中正确的是( ),
A.对角线相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形
D.对角线互相垂直的平行四边形是菱形
解析:选项A,B不能判定是菱形;选项C,对角线相等的平行四边形应 是矩形,所以C错误,故选D.
答案:D
2.(2011·江苏无锡中考)菱形具有而矩形不一定具有的性质是( ).
A.对角线互相垂直
B.对角线相等
C.对角线互相平分
D.对角互补
答案:A
3.如图所示,在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的边 长为( ).
A.5
B.6
C.8
D.10
解析:因为菱形的对角线互相垂直且平分,所以在Rt△AOB中,根据勾 股定理可得AB= = =5,即菱形的边长为5.
答案:A
4.如图,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周 长为( ).
A.20 B.18
C.16 D.15
解析:由题意可知,△ABC是等边三角形,
所以AB=BC=AC=4.
因为菱形的四条边都相等,故菱形ABCD的周长为16.
答案:C
5.(2011·广州中考)如图,AC是菱形ABCD的对角线,点E,F分别在边 AB,AD上,且AE=AF.
求证:△ACE≌△ACF.
证明:∵四边形ABCD为菱形,
∴∠BAC=∠DAC.
又∵AE=AF,AC=AC,
∴△ACE≌△ACF(SAS).
6.已知在菱形ABCD中,O是对角线BD上的一动点.如图,P为线段BC 上一点,连接PO,并延长交AD于点Q,当O是BD的中点时,求证:OP= OQ.
证明:∵四边形ABCD为菱形,∴AD∥BC.
∴∠OBP=∠ODQ.
∵O是BD的中点,∴OB=OD.
在△BOP和△DOQ中,
∵∠OBP=∠ODQ,OB=OD,∠BOP=∠DOQ,
∴△BOP≌△DOQ(ASA),∴OP=OQ.
7.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
解:(1)四边形OCED是菱形.理由如下:
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又在矩形ABCD中,OC=OD,
∴四边形OCED是菱形.
(2)连接OE,由菱形OCED得CD⊥OE,
∴OE∥BC.
又CE∥BD,∴四边形BCEO是平行四边形.
∴OE=BC=8,
∴S四边形OCED= OE·CD= ×8×6=24.
