函数的图象的变换,反函数,函数的定义域和值域(四个课件)
文档属性
| 名称 | 函数的图象的变换,反函数,函数的定义域和值域(四个课件) |
|
|
| 格式 | zip | ||
| 文件大小 | 641.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-28 00:00:00 | ||
图片预览


文档简介
(共4张PPT)
函数图象的变换
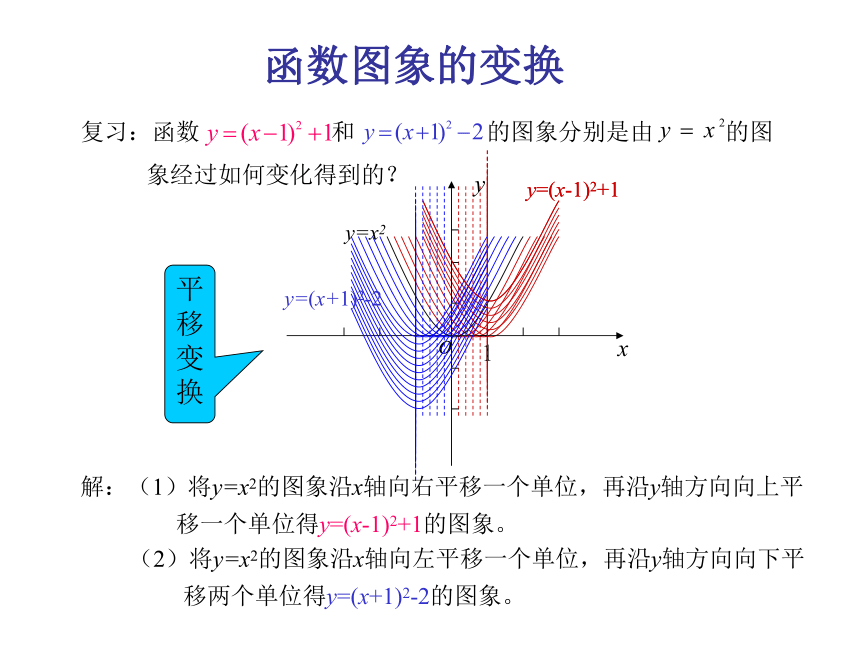
复习:函数 和 的图象分别是由 的图
象经过如何变化得到的?
平移变换
解:(1)将y=x2的图象沿x轴向右平移一个单位,再沿y轴方向向上平
移一个单位得y=(x-1)2+1的图象。
(2)将y=x2的图象沿x轴向左平移一个单位,再沿y轴方向向下平
移两个单位得y=(x+1)2-2的图象。
y=(x-1)2+1
o
y
x
1
y=x2
y=(x+1)2-2
y=(x-1)2+1
函数图象的变换
小结(平移变换):
1. 将函数y=f(x)的图象向左(或向右)平移|k|个单位(k>0时向左,k<0向右)得y=f(x+k)的图象。
2. 将函数y=f(x)的图象向上(或向下)平移|k|个单位(k>0时向上,k<0向下)得y=f(x) +k的图象。
函数图象的变换
例1. 画出函数 的图象。
解:
怎么办呢?
平移变换
因此:我们可将函数 的图象先沿x轴向左平移2个单位,再沿y轴向上平移3个单位得到函数 的图象。
y
x
o
好象学过
的图象!
…
函数图象的变换
例2. 设f(x)= (x>0),求函数y=-f(x)、y=f(-x)、y=-f(-x)的解析式及其定义域,并分别作出它们的图象。
x
x
y
o
1
y=f(x)
x
x
y
o
1
y=f(x)
x
x
y
o
1
y=f(x)
y=-f(x)
y=f(-x)
y=-f(-x)
横坐标不变
纵坐标取相反数
横坐标取相反数
纵坐标不变
横坐标、纵坐标
同时取相反数
图象关于x轴对称
图象关于y轴对称
图象关于原点对称
对称变换
函数图象的变换
复习:函数 和 的图象分别是由 的图
象经过如何变化得到的?
平移变换
解:(1)将y=x2的图象沿x轴向右平移一个单位,再沿y轴方向向上平
移一个单位得y=(x-1)2+1的图象。
(2)将y=x2的图象沿x轴向左平移一个单位,再沿y轴方向向下平
移两个单位得y=(x+1)2-2的图象。
y=(x-1)2+1
o
y
x
1
y=x2
y=(x+1)2-2
y=(x-1)2+1
函数图象的变换
小结(平移变换):
1. 将函数y=f(x)的图象向左(或向右)平移|k|个单位(k>0时向左,k<0向右)得y=f(x+k)的图象。
2. 将函数y=f(x)的图象向上(或向下)平移|k|个单位(k>0时向上,k<0向下)得y=f(x) +k的图象。
函数图象的变换
例1. 画出函数 的图象。
解:
怎么办呢?
平移变换
因此:我们可将函数 的图象先沿x轴向左平移2个单位,再沿y轴向上平移3个单位得到函数 的图象。
y
x
o
好象学过
的图象!
…
函数图象的变换
例2. 设f(x)= (x>0),求函数y=-f(x)、y=f(-x)、y=-f(-x)的解析式及其定义域,并分别作出它们的图象。
x
x
y
o
1
y=f(x)
x
x
y
o
1
y=f(x)
x
x
y
o
1
y=f(x)
y=-f(x)
y=f(-x)
y=-f(-x)
横坐标不变
纵坐标取相反数
横坐标取相反数
纵坐标不变
横坐标、纵坐标
同时取相反数
图象关于x轴对称
图象关于y轴对称
图象关于原点对称
对称变换
