18.1《勾股定理》课件(人教版八年级下)
文档属性
| 名称 | 18.1《勾股定理》课件(人教版八年级下) |  | |
| 格式 | zip | ||
| 文件大小 | 233.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-28 18:35:56 | ||
图片预览








文档简介
(共22张PPT)
第十八章 勾股定理
18.1 勾股定理
1.直角三角形的两锐角____.
学 前 温 故
2.在直角三角形中,30°角所对的直角边等于斜边的____.
互余
一半
1.勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那 么 .
答案:a2+b2=c2
新 课 早 知
2.已知直角三角形的两直角边长分别是5和6,则斜边长的平方是 .
答案:61
3.证明勾股定理的方法: ,如“赵爽弦图”等.
答案:面积法
4.数轴上的点可以表示 ,也可以表示 ,长为 的线段是直角边长分别为正整数 , 的直
角三角形的斜边长.
答案:有理数 无理数 1 4
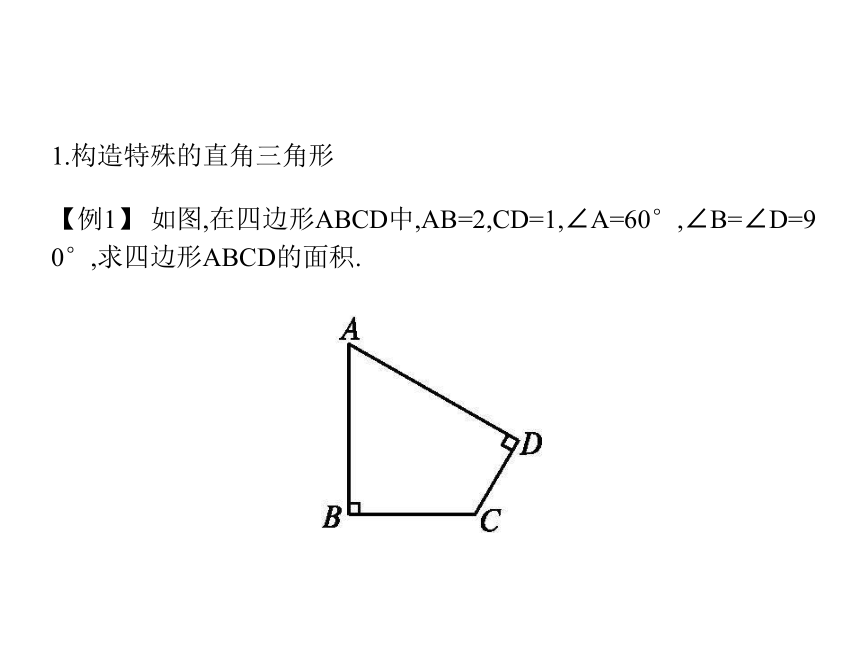
1.构造特殊的直角三角形
【例1】 如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,∠B=∠D=9 0°,求四边形ABCD的面积.
解:如图所示,延长AD,BC相交于点E,
∵∠A=60°,∠B=90°,
∴∠E=30°.
在Rt△CDE中,∠CDE=90°,CD=1,
∴CE=2.
DE= = = .
故S△CDE= CD·DE= ×1× = .
在Rt△ABE中,∠ABE=90°,∠E=30°,
∴AE=2AB=2×2=4,
BE= = =2 .
∴S△ABE= AB·BE= ×2×2 =2 .
∴S四边形ABCD=S△ABE-S△CDE=2 - = .
点拨:求不规则图形的面积,关键是用割补法将其转化为规则图形,然 后再求其面积.
2.勾股定理的实际应用
【例2】 有一立方体礼盒如图所示,在底部A处有一只壁虎,C'处有一 只蚊子,壁虎急于捕捉到蚊子充饥.
(1)试确定壁虎所走的最短路线;
(2)若立方体礼盒的棱长为20 cm,壁虎要在半分钟内捕捉到蚊子,求 壁虎每分钟至少爬行多少厘米 (保留整数)
解:(1)若把礼盒的上底面A'B'C'D'竖立起来,如图所示,使它与立方体 的正面(ABB'A')在同一平面内,然后连接AC',根据“两点间线段最 短”知,线段AC'就是壁虎捕捉蚊子所走的最短路线.
(2)由(1)得,△ABC'是直角三角形,且AB=20,BC'=40.
根据勾股定理,得AC'= = ≈44.7(cm).
1.三个正方形的面积如图所示,则正方形A的边长是 ( ).
A.6 B.36
C.64 D.8
答案:A
解析:由勾股定理可知,以两直角边为边长的正方形的面积和=以斜 边为边长的正方形的面积,即64+SA=100,SA=36,所以正方形A的边长 为6.故选A.
2.如图,在△ABC中,∠A=150°,AB=20 cm,AC=30 cm,则△ABC的面积 等于( ).
A.450 cm2 B.300 cm2
C.330 cm2 D.150 cm2
∵∠BAC=150°,
∴∠DAC=30°.
在Rt△ACD中,∠DAC=30°,
∴CD= AC= ×30=15(cm).
∴S△ABC= AB·CD= ×20×15=150(cm2),故选D.
答案:D
解析:过点C作CD⊥AB,垂足为D,
3.(2011·广东肇庆中考)在直角△ABC中,∠C=90°,BC=12,AC=9,则 AB= .
答案:15
4.下图是一个外轮廓为长方形的机器零件平面示意图,根据图中的 尺寸(单位:mm),计算两圆孔中心A和B的距离为 mm.
解析:AC=90,BC=120,
∴AB= =150(mm).
答案:150
5.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角 形与中间的一个小正方形拼成的一个大正方形(如图所示).直角三 角形的两直角边长分别为a,b(a
(1)请你运用本图验证勾股定理;
(2)如果大正方形的面积是13,小正方形的面积是1,试求(a+b)2的值.
解:(1)大正方形的面积为c2,中间部分小正方形的面积为(b-a)2,四个直 角三角形的面积和为4× ab.由图形关系,知大正方形面积=小正方形
面积+四个直角三角形面积,即有c2=(b-a)2+4× ab=b2-2ab+a2+2ab=a2+b2.
(2)由大正方形的面积是13,小正方形的面积是1,得每个三角形的面 积是3,
所以 ab=3,ab=6.
又∵c2=13,∴a2+b2=13.
∴(a+b)2=a2+b2+2ab=13+12=25.
∴(a+b)2=25.
第十八章 勾股定理
18.1 勾股定理
1.直角三角形的两锐角____.
学 前 温 故
2.在直角三角形中,30°角所对的直角边等于斜边的____.
互余
一半
1.勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那 么 .
答案:a2+b2=c2
新 课 早 知
2.已知直角三角形的两直角边长分别是5和6,则斜边长的平方是 .
答案:61
3.证明勾股定理的方法: ,如“赵爽弦图”等.
答案:面积法
4.数轴上的点可以表示 ,也可以表示 ,长为 的线段是直角边长分别为正整数 , 的直
角三角形的斜边长.
答案:有理数 无理数 1 4
1.构造特殊的直角三角形
【例1】 如图,在四边形ABCD中,AB=2,CD=1,∠A=60°,∠B=∠D=9 0°,求四边形ABCD的面积.
解:如图所示,延长AD,BC相交于点E,
∵∠A=60°,∠B=90°,
∴∠E=30°.
在Rt△CDE中,∠CDE=90°,CD=1,
∴CE=2.
DE= = = .
故S△CDE= CD·DE= ×1× = .
在Rt△ABE中,∠ABE=90°,∠E=30°,
∴AE=2AB=2×2=4,
BE= = =2 .
∴S△ABE= AB·BE= ×2×2 =2 .
∴S四边形ABCD=S△ABE-S△CDE=2 - = .
点拨:求不规则图形的面积,关键是用割补法将其转化为规则图形,然 后再求其面积.
2.勾股定理的实际应用
【例2】 有一立方体礼盒如图所示,在底部A处有一只壁虎,C'处有一 只蚊子,壁虎急于捕捉到蚊子充饥.
(1)试确定壁虎所走的最短路线;
(2)若立方体礼盒的棱长为20 cm,壁虎要在半分钟内捕捉到蚊子,求 壁虎每分钟至少爬行多少厘米 (保留整数)
解:(1)若把礼盒的上底面A'B'C'D'竖立起来,如图所示,使它与立方体 的正面(ABB'A')在同一平面内,然后连接AC',根据“两点间线段最 短”知,线段AC'就是壁虎捕捉蚊子所走的最短路线.
(2)由(1)得,△ABC'是直角三角形,且AB=20,BC'=40.
根据勾股定理,得AC'= = ≈44.7(cm).
1.三个正方形的面积如图所示,则正方形A的边长是 ( ).
A.6 B.36
C.64 D.8
答案:A
解析:由勾股定理可知,以两直角边为边长的正方形的面积和=以斜 边为边长的正方形的面积,即64+SA=100,SA=36,所以正方形A的边长 为6.故选A.
2.如图,在△ABC中,∠A=150°,AB=20 cm,AC=30 cm,则△ABC的面积 等于( ).
A.450 cm2 B.300 cm2
C.330 cm2 D.150 cm2
∵∠BAC=150°,
∴∠DAC=30°.
在Rt△ACD中,∠DAC=30°,
∴CD= AC= ×30=15(cm).
∴S△ABC= AB·CD= ×20×15=150(cm2),故选D.
答案:D
解析:过点C作CD⊥AB,垂足为D,
3.(2011·广东肇庆中考)在直角△ABC中,∠C=90°,BC=12,AC=9,则 AB= .
答案:15
4.下图是一个外轮廓为长方形的机器零件平面示意图,根据图中的 尺寸(单位:mm),计算两圆孔中心A和B的距离为 mm.
解析:AC=90,BC=120,
∴AB= =150(mm).
答案:150
5.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角 形与中间的一个小正方形拼成的一个大正方形(如图所示).直角三 角形的两直角边长分别为a,b(a
(1)请你运用本图验证勾股定理;
(2)如果大正方形的面积是13,小正方形的面积是1,试求(a+b)2的值.
解:(1)大正方形的面积为c2,中间部分小正方形的面积为(b-a)2,四个直 角三角形的面积和为4× ab.由图形关系,知大正方形面积=小正方形
面积+四个直角三角形面积,即有c2=(b-a)2+4× ab=b2-2ab+a2+2ab=a2+b2.
(2)由大正方形的面积是13,小正方形的面积是1,得每个三角形的面 积是3,
所以 ab=3,ab=6.
又∵c2=13,∴a2+b2=13.
∴(a+b)2=a2+b2+2ab=13+12=25.
∴(a+b)2=25.
