18.2《勾股定理的逆定理》课件(人教版八年级下)
文档属性
| 名称 | 18.2《勾股定理的逆定理》课件(人教版八年级下) |  | |
| 格式 | zip | ||
| 文件大小 | 228.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-28 18:35:56 | ||
图片预览








文档简介
(共25张PPT)
18.2 勾股定理的逆定理
勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 ____________.
学 前 温 故
a2+b2=c2
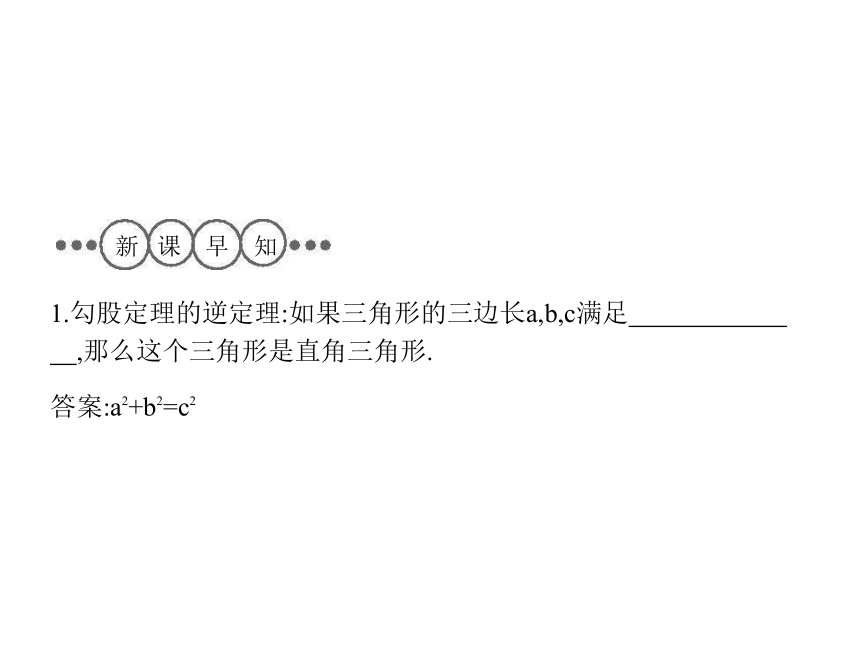
1.勾股定理的逆定理:如果三角形的三边长a,b,c满足 ,那么这个三角形是直角三角形.
答案:a2+b2=c2
新 课 早 知
2.△ABC的三边分别为a=1.2 cm,b=1.6 cm,c=2 cm,则∠C是( ).
A.锐角
B.直角
C.钝角
D.以上三种都有可能
答案:B
4.一般地,如果一个定理的逆命题经过证明是正确的,它也是一个定 理,称这两个定理互为 .
答案:逆定理
3.如果两个命题的题设和结论正好相反,那么这样的两个命题叫做 .如果把其中一个叫做 ,那么另一个叫做它的 .
答案:互逆命题 原命题 逆命题
5.下列真命题中,其逆命题也是真命题的是 ( ).
A.直角都相等
B.等边三角形是锐角三角形
C.若a|b|
D.如果a=b或a=-b,那么a2=b2
答案:D
1.求不规则图形的面积
【例1】 如图所示,已知在四边形ABCD中,AB=1,BC=2,CD=2,AD=3, 且AB⊥BC,求四边形ABCD的面积.
分析:要求四边形ABCD的面积,可以转化为两个三角形面积之和,因 为AB⊥BC,所以连接AC,则△ABC为直角三角形.同时,根据勾股定 理的逆定理可证明△ACD也为直角三角形,故四边形ABCD的面积 等于Rt△ABC和Rt△ACD的面积之和.
在Rt△ABC中,AC2=AB2+BC2=12+22=5,
所以AC= .在△ACD中,因为AC2+CD2= +22=9,AD2=32=9,
所以AC2+CD2=AD2,
所以∠ACD=90°.
因为S△ABC= ×1×2=1,S△ACD= × ×2= ,所以S四边形ABCD=S△ABC+S△ACD=
1+ .
点拨:勾股定理的逆定理给我们提供了一种证明一个角是直角的方 法,即通过计算两条较短的边的平方和是否等于第三边的平方来判 断三角形是否有一个角是直角.
解:连接AC,
2.勾股定理的逆定理的实际应用
【例2】 如图,南北向MN以西为我国领海,以东为公海.上午9时50 分,我国反走私A艇发现正东方向有一走私艇C以13海里/时的速度 偷偷向我国领海开来,便立即通知正在MN线上巡逻的我国反走私 艇B.已知A,C两艇的距离是13海里,A,B两艇的距离是5海里;反走私 B艇测得离C艇的距离是12海里.若走私艇C的速度不变,最早会在什 么时间进入我国领海
分析:为减小思考问题的“跨度”,可将原问题分解成下述“子问题”:(1)△ABC是什么类型的三角形 (2)走私艇C进入我国领海的最近 距离是多少 (3)走私艇C最早会在什么时间进入 这样问题就可迎刃 而解.
解:设MN交AC于点E,
则∠BEC=90°.
又AB2+BC2=52+122=169=132=AC2,
∴△ABC是直角三角形,∠ABC=90°.
又∵MN⊥CE,
∴走私艇C进入我国领海的最近距离是CE.
则CE2+BE2=144,(13-CE)2+BE2=25,得26CE=288.
∴CE= .
÷13= ≈0.85(小时),0.85×60=51(分).9时50分+51分=10时41分.
答:走私艇C最早约在10时41分进入我国领海.
点拨:将实际问题转化成几何问题是常用的数学方法.此题还可先用 面积方法求BE,再用勾股定理求EC.
1.△ABC在下列条件下,不是直角三角形的是 ( ).
A.a2=b2-c2
B.a∶b∶c=3∶4∶5
C.∠C=∠B+∠A
D.∠A∶∠B∶∠C=3∶4∶5
答案:D
2.在△ABC中,AB=12 cm,BC=16 cm,AC=20 cm,则△ABC的面积是 ( ).
A.96 cm2 B.120 cm2
C.160 cm2 D.200 cm2
答案:A
3.△ABC的三边a,b,c满足(a-b)(a2+b2-c2)=0,则△ABC是( ).
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
解析:由已知可得a-b=0或a2+b2-c2=0,即a=b或a2+b2=c2,所以此三角形 是等腰三角形或直角三角形,选D.
答案:D
4.(2011·四川凉山中考)把命题“如果直角三角形的两直角边长分别 为a,b,斜边长为c,那么a2+b2=c2”的逆命题写成“如果……,那么……”的形式: .
答案:如果三角形的三边长分别为a,b,c,且满足a2+b2=c2,那么这个三 角形是直角三角形
5.如图,在正方形网格中,若小方格的边长为1,则△ABC是 三角形.
解析:根据勾股定理可求得AC= ,AB= ,BC= ,因为( )2+
( )2=( )2,
即AC2+AB2=BC2,
∴△ABC是直角三角形.
答案:直角
6.如图,三个村庄A,B,C之间的距离分别为AB=5 km,BC=12 km,AC=1 3 km.要从B修一条公路BD直达AC.已知公路的造价为26 000元/km, 求修这条公路的最低造价是多少
解:∵52+122=132,
∴AB2+BC2=AC2.
∴△ABC是直角三角形.
∴BD·CA=BC·BA.
∴BD= = (km).
∴修这条公路的最低造价为 ×26 000=120 000(元).
7.如图所示,在河岸l的同侧有A,B两村,C为河岸上一供水站,CA,CB 为供水管道,现已测得AC=12 km,BC=5 km,两村的距离为13 km,∠α= 30°,若有一人从C处出发,沿河岸行走,速度为1.5 km/h,问多长时间后 距A最近
解:过A作AD⊥l,垂足为D.
在△ABC中,BC2+AC2=52+122=132=AB2,
∴∠ACB=90°.
∴∠ACD=180°-∠α-∠ACB=180°-30°-90°=60°,
∴∠CAD=90°-∠ACD=30°.
在Rt△ADC中,CD= AC= ×12=6(km),6÷1.5=4(h).
答:4 h后距A最近.
18.2 勾股定理的逆定理
勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 ____________.
学 前 温 故
a2+b2=c2
1.勾股定理的逆定理:如果三角形的三边长a,b,c满足 ,那么这个三角形是直角三角形.
答案:a2+b2=c2
新 课 早 知
2.△ABC的三边分别为a=1.2 cm,b=1.6 cm,c=2 cm,则∠C是( ).
A.锐角
B.直角
C.钝角
D.以上三种都有可能
答案:B
4.一般地,如果一个定理的逆命题经过证明是正确的,它也是一个定 理,称这两个定理互为 .
答案:逆定理
3.如果两个命题的题设和结论正好相反,那么这样的两个命题叫做 .如果把其中一个叫做 ,那么另一个叫做它的 .
答案:互逆命题 原命题 逆命题
5.下列真命题中,其逆命题也是真命题的是 ( ).
A.直角都相等
B.等边三角形是锐角三角形
C.若a
D.如果a=b或a=-b,那么a2=b2
答案:D
1.求不规则图形的面积
【例1】 如图所示,已知在四边形ABCD中,AB=1,BC=2,CD=2,AD=3, 且AB⊥BC,求四边形ABCD的面积.
分析:要求四边形ABCD的面积,可以转化为两个三角形面积之和,因 为AB⊥BC,所以连接AC,则△ABC为直角三角形.同时,根据勾股定 理的逆定理可证明△ACD也为直角三角形,故四边形ABCD的面积 等于Rt△ABC和Rt△ACD的面积之和.
在Rt△ABC中,AC2=AB2+BC2=12+22=5,
所以AC= .在△ACD中,因为AC2+CD2= +22=9,AD2=32=9,
所以AC2+CD2=AD2,
所以∠ACD=90°.
因为S△ABC= ×1×2=1,S△ACD= × ×2= ,所以S四边形ABCD=S△ABC+S△ACD=
1+ .
点拨:勾股定理的逆定理给我们提供了一种证明一个角是直角的方 法,即通过计算两条较短的边的平方和是否等于第三边的平方来判 断三角形是否有一个角是直角.
解:连接AC,
2.勾股定理的逆定理的实际应用
【例2】 如图,南北向MN以西为我国领海,以东为公海.上午9时50 分,我国反走私A艇发现正东方向有一走私艇C以13海里/时的速度 偷偷向我国领海开来,便立即通知正在MN线上巡逻的我国反走私 艇B.已知A,C两艇的距离是13海里,A,B两艇的距离是5海里;反走私 B艇测得离C艇的距离是12海里.若走私艇C的速度不变,最早会在什 么时间进入我国领海
分析:为减小思考问题的“跨度”,可将原问题分解成下述“子问题”:(1)△ABC是什么类型的三角形 (2)走私艇C进入我国领海的最近 距离是多少 (3)走私艇C最早会在什么时间进入 这样问题就可迎刃 而解.
解:设MN交AC于点E,
则∠BEC=90°.
又AB2+BC2=52+122=169=132=AC2,
∴△ABC是直角三角形,∠ABC=90°.
又∵MN⊥CE,
∴走私艇C进入我国领海的最近距离是CE.
则CE2+BE2=144,(13-CE)2+BE2=25,得26CE=288.
∴CE= .
÷13= ≈0.85(小时),0.85×60=51(分).9时50分+51分=10时41分.
答:走私艇C最早约在10时41分进入我国领海.
点拨:将实际问题转化成几何问题是常用的数学方法.此题还可先用 面积方法求BE,再用勾股定理求EC.
1.△ABC在下列条件下,不是直角三角形的是 ( ).
A.a2=b2-c2
B.a∶b∶c=3∶4∶5
C.∠C=∠B+∠A
D.∠A∶∠B∶∠C=3∶4∶5
答案:D
2.在△ABC中,AB=12 cm,BC=16 cm,AC=20 cm,则△ABC的面积是 ( ).
A.96 cm2 B.120 cm2
C.160 cm2 D.200 cm2
答案:A
3.△ABC的三边a,b,c满足(a-b)(a2+b2-c2)=0,则△ABC是( ).
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
解析:由已知可得a-b=0或a2+b2-c2=0,即a=b或a2+b2=c2,所以此三角形 是等腰三角形或直角三角形,选D.
答案:D
4.(2011·四川凉山中考)把命题“如果直角三角形的两直角边长分别 为a,b,斜边长为c,那么a2+b2=c2”的逆命题写成“如果……,那么……”的形式: .
答案:如果三角形的三边长分别为a,b,c,且满足a2+b2=c2,那么这个三 角形是直角三角形
5.如图,在正方形网格中,若小方格的边长为1,则△ABC是 三角形.
解析:根据勾股定理可求得AC= ,AB= ,BC= ,因为( )2+
( )2=( )2,
即AC2+AB2=BC2,
∴△ABC是直角三角形.
答案:直角
6.如图,三个村庄A,B,C之间的距离分别为AB=5 km,BC=12 km,AC=1 3 km.要从B修一条公路BD直达AC.已知公路的造价为26 000元/km, 求修这条公路的最低造价是多少
解:∵52+122=132,
∴AB2+BC2=AC2.
∴△ABC是直角三角形.
∴BD·CA=BC·BA.
∴BD= = (km).
∴修这条公路的最低造价为 ×26 000=120 000(元).
7.如图所示,在河岸l的同侧有A,B两村,C为河岸上一供水站,CA,CB 为供水管道,现已测得AC=12 km,BC=5 km,两村的距离为13 km,∠α= 30°,若有一人从C处出发,沿河岸行走,速度为1.5 km/h,问多长时间后 距A最近
解:过A作AD⊥l,垂足为D.
在△ABC中,BC2+AC2=52+122=132=AB2,
∴∠ACB=90°.
∴∠ACD=180°-∠α-∠ACB=180°-30°-90°=60°,
∴∠CAD=90°-∠ACD=30°.
在Rt△ADC中,CD= AC= ×12=6(km),6÷1.5=4(h).
答:4 h后距A最近.
