19.1.2《平行四边形的判定》课件(人教版八年级下)
文档属性
| 名称 | 19.1.2《平行四边形的判定》课件(人教版八年级下) |  | |
| 格式 | zip | ||
| 文件大小 | 248.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-28 18:35:56 | ||
图片预览








文档简介
(共23张PPT)
19.1.2 平行四边形的判定
1.点到直线的距离:点到这条直线的_______的长度.
学 前 温 故
2.平行线的判定:(1)同位角____,两直线平行;
(2)内错角____;两直线平行;
(3)同旁内角____,两直线平行.
3.平行四边形的定义:有两组对边分别____的四边形叫做平行四边 形.
垂线段
相等
相等
互补
平行
4.平行四边形的性质:
(1)平行四边形的两组对边分别____;
(2)平行四边形的两组对边分别______;
(3)平行四边形的两组对角分别_____;
(4)平行四边形的对角线___________.
平行
相等
相等
互相平分
1.平行四边形的判定定理
(1)两组对边分别 的四边形是平行四边形;对角线 的四边形是平行四边形.
(2)两组对角分别 的四边形是平行四边形.
(3)一组对边 的四边形是平行四边形.
答案:(1)相等 互相平分 (2)相等 (3)平行且相等
新 课 早 知
2.能够判定四边形ABCD是平行四边形的条件是( ).
A.AB∥CD,AD=BC
B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC
D.AB=AD,CB=CD
答案:C
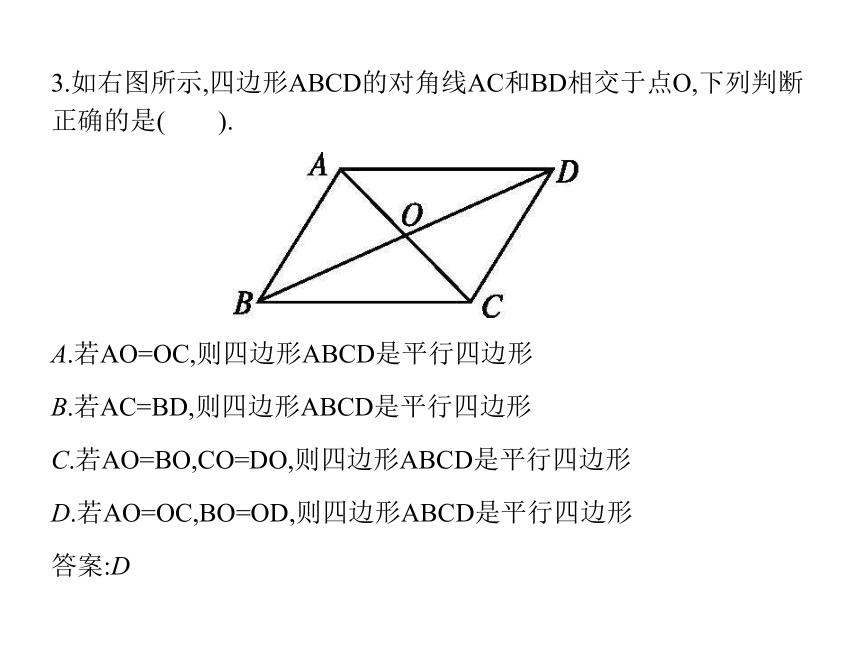
3.如右图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断 正确的是( ).
A.若AO=OC,则四边形ABCD是平行四边形
B.若AC=BD,则四边形ABCD是平行四边形
C.若AO=BO,CO=DO,则四边形ABCD是平行四边形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
答案:D
4.连接三角形两边 的线段叫做三角形的中位线.
答案:中点
5.三角形中位线定理
三角形的中位线 于三角形的第三边,且等于第三边的 .
答案:平行 一半
6.已知在△ABC中,BC=6 cm,E,F分别是AB,AC的中点,那么EF的长是 cm.
答案:3
7.两条平行线间的任何两条平行线段都 .
答案:相等
1.平行四边形的性质与判定的综合应用
【例1】 已知,如图所示,AD为△ABC的中线,E为AC上一点,连接BE 交AD于F,且AE=FE.
求证:BF=AC.
分析:延长AD到N,使DN=AD,构造出平行四边形ABNC求解即可.
证明:延长AD到N,使DN=AD,连接BN,CN,
∵BD=CD,AD=ND,∴四边形ABNC是平行四边形.
∴BN=AC,BN∥AC.
∴∠FAE=∠BND.
∵AE=FE,∴∠FAE=∠AFE.
∵∠AFE=∠BFD,∠FAE=∠BND,
∴∠BFD=∠BND,
∴BN=BF.∴BF=AC.
点拨:有三角形中线时,常延长中线构造平行四边形,然后再利用平行 四边形的性质转化线段或角的相等进行证题.
2.三角形中位线定理的运用
【例2】 如图所示,已知E,F,G,H分别是线段AB,BD,CD,CA的中点, 求证:四边形EFGH是平行四边形.
分析:本题出现多个中点,应想到三角形中位线.
E,H分别为AB,AC的中点,那么连接BC后,EH为△ABC的中位线,可 利用中位线证明.
证明:连接BC,AD,∵H为AC的中点,E为AB的中点,
∴EH∥BC,EH= BC.
又∵G为CD的中点,F为BD的中点,
∴GF∥BC,GF= BC.
∴EH∥GF且EH=GF.
∴四边形EFGH为平行四边形.
点拨:当题目中已知线段的中点时,一般应考虑运用三角形的中位线 定理,取中点构造中位线是作辅助线的常用方法.
1.下列条件不能判断四边形ABCD是平行四边形的是( ).
A.∠A=∠C,∠B=∠D
B.AD=BC,AB=CD
C.AB=CD,AD∥BC
D.AB∥CD,AD∥BC
解析:一组对边平行且相等的四边形是平行四边形,故C错误.
答案:C
2.小明的爸爸在钉制平行四边形框架时,采用了一种方法:将两根木 条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边 形,这种方法的依据是( ).
A.两组对边分别平行的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.两组对角分别相等的四边形是平行四边形
答案:B
3.(2011·山东德州中考)如图,D,E,F分别为△ABC三边的中点,则图中 平行四边形的个数为 .
解析:由三角形的中位线定理得,DE∥AC,DF∥BC,EF∥AB.所以由 平行四边形的定义得,四边形ADEF、四边形BEFD、四边形ECFD 是平行四边形.
答案:3
4.在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则可 添加的条件为 .(填一个即可)
答案:答案不唯一,如AB=CD或∠A=∠C或AD∥BC
5.在 ABCD中,分别以AD,BC为边向内作等边△ADE和等边△ BCF,连接BE,DF.求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠DAB=∠BCD.
又∵△ADE和△CBF都是等边三角形,
∴DE=BF,AE=CF,∠DAE=∠BCF=60°.
∵∠DCF=∠BCD-∠BCF,∠BAE=∠DAB-∠DAE,∴∠DCF=∠ BAE.
∴△DCF≌△BAE(SAS).∴DF=BE.
∴四边形BEDF是平行四边形.
6.如图,在 ABCD中,点E是AD的中点,BE的延长线与CD的延长线 相交于点F.
(1)求证:△ABE≌△DFE;
(2)连接BD,AF,判断四边形ABDF的形状,并证明你的结论.
分析:(1)应用平行四边形的性质证三角形全等.
(2)可由AE=DE,再证BE=FE.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.∴∠BAD=∠EDF,∠ABE=∠DFE.
又∵E是AD的中点,∴AE=DE.
∴△ABE≌△DFE(AAS).
(2)解:四边形ABDF是平行四边形.证明如下:
∵△ABE≌△DFE,
∴BE=FE.
又AE=ED,∴四边形ABDF是平行四边形.
19.1.2 平行四边形的判定
1.点到直线的距离:点到这条直线的_______的长度.
学 前 温 故
2.平行线的判定:(1)同位角____,两直线平行;
(2)内错角____;两直线平行;
(3)同旁内角____,两直线平行.
3.平行四边形的定义:有两组对边分别____的四边形叫做平行四边 形.
垂线段
相等
相等
互补
平行
4.平行四边形的性质:
(1)平行四边形的两组对边分别____;
(2)平行四边形的两组对边分别______;
(3)平行四边形的两组对角分别_____;
(4)平行四边形的对角线___________.
平行
相等
相等
互相平分
1.平行四边形的判定定理
(1)两组对边分别 的四边形是平行四边形;对角线 的四边形是平行四边形.
(2)两组对角分别 的四边形是平行四边形.
(3)一组对边 的四边形是平行四边形.
答案:(1)相等 互相平分 (2)相等 (3)平行且相等
新 课 早 知
2.能够判定四边形ABCD是平行四边形的条件是( ).
A.AB∥CD,AD=BC
B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC
D.AB=AD,CB=CD
答案:C
3.如右图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断 正确的是( ).
A.若AO=OC,则四边形ABCD是平行四边形
B.若AC=BD,则四边形ABCD是平行四边形
C.若AO=BO,CO=DO,则四边形ABCD是平行四边形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
答案:D
4.连接三角形两边 的线段叫做三角形的中位线.
答案:中点
5.三角形中位线定理
三角形的中位线 于三角形的第三边,且等于第三边的 .
答案:平行 一半
6.已知在△ABC中,BC=6 cm,E,F分别是AB,AC的中点,那么EF的长是 cm.
答案:3
7.两条平行线间的任何两条平行线段都 .
答案:相等
1.平行四边形的性质与判定的综合应用
【例1】 已知,如图所示,AD为△ABC的中线,E为AC上一点,连接BE 交AD于F,且AE=FE.
求证:BF=AC.
分析:延长AD到N,使DN=AD,构造出平行四边形ABNC求解即可.
证明:延长AD到N,使DN=AD,连接BN,CN,
∵BD=CD,AD=ND,∴四边形ABNC是平行四边形.
∴BN=AC,BN∥AC.
∴∠FAE=∠BND.
∵AE=FE,∴∠FAE=∠AFE.
∵∠AFE=∠BFD,∠FAE=∠BND,
∴∠BFD=∠BND,
∴BN=BF.∴BF=AC.
点拨:有三角形中线时,常延长中线构造平行四边形,然后再利用平行 四边形的性质转化线段或角的相等进行证题.
2.三角形中位线定理的运用
【例2】 如图所示,已知E,F,G,H分别是线段AB,BD,CD,CA的中点, 求证:四边形EFGH是平行四边形.
分析:本题出现多个中点,应想到三角形中位线.
E,H分别为AB,AC的中点,那么连接BC后,EH为△ABC的中位线,可 利用中位线证明.
证明:连接BC,AD,∵H为AC的中点,E为AB的中点,
∴EH∥BC,EH= BC.
又∵G为CD的中点,F为BD的中点,
∴GF∥BC,GF= BC.
∴EH∥GF且EH=GF.
∴四边形EFGH为平行四边形.
点拨:当题目中已知线段的中点时,一般应考虑运用三角形的中位线 定理,取中点构造中位线是作辅助线的常用方法.
1.下列条件不能判断四边形ABCD是平行四边形的是( ).
A.∠A=∠C,∠B=∠D
B.AD=BC,AB=CD
C.AB=CD,AD∥BC
D.AB∥CD,AD∥BC
解析:一组对边平行且相等的四边形是平行四边形,故C错误.
答案:C
2.小明的爸爸在钉制平行四边形框架时,采用了一种方法:将两根木 条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边 形,这种方法的依据是( ).
A.两组对边分别平行的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.两组对角分别相等的四边形是平行四边形
答案:B
3.(2011·山东德州中考)如图,D,E,F分别为△ABC三边的中点,则图中 平行四边形的个数为 .
解析:由三角形的中位线定理得,DE∥AC,DF∥BC,EF∥AB.所以由 平行四边形的定义得,四边形ADEF、四边形BEFD、四边形ECFD 是平行四边形.
答案:3
4.在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则可 添加的条件为 .(填一个即可)
答案:答案不唯一,如AB=CD或∠A=∠C或AD∥BC
5.在 ABCD中,分别以AD,BC为边向内作等边△ADE和等边△ BCF,连接BE,DF.求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠DAB=∠BCD.
又∵△ADE和△CBF都是等边三角形,
∴DE=BF,AE=CF,∠DAE=∠BCF=60°.
∵∠DCF=∠BCD-∠BCF,∠BAE=∠DAB-∠DAE,∴∠DCF=∠ BAE.
∴△DCF≌△BAE(SAS).∴DF=BE.
∴四边形BEDF是平行四边形.
6.如图,在 ABCD中,点E是AD的中点,BE的延长线与CD的延长线 相交于点F.
(1)求证:△ABE≌△DFE;
(2)连接BD,AF,判断四边形ABDF的形状,并证明你的结论.
分析:(1)应用平行四边形的性质证三角形全等.
(2)可由AE=DE,再证BE=FE.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.∴∠BAD=∠EDF,∠ABE=∠DFE.
又∵E是AD的中点,∴AE=DE.
∴△ABE≌△DFE(AAS).
(2)解:四边形ABDF是平行四边形.证明如下:
∵△ABE≌△DFE,
∴BE=FE.
又AE=ED,∴四边形ABDF是平行四边形.
