16.1.2《分式的基本性质》课件1(人教版八年级下)
文档属性
| 名称 | 16.1.2《分式的基本性质》课件1(人教版八年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 350.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-28 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
16.1.2 分式的基本性质
1.分数的基本性质
分数的分子和分母都乘(或除以)同一个________的数,分数的值不变.
2.分数的通分
把几个异分母的分数化为同分母的分数叫做分数的通分,最简公分母取各 个分母的______________.
学 前 温 故
不等于0
最小公倍数
3.最简分数
分子、分母是互质的分数,即分子和分母的最大公因数是1,这样的分数叫 做最简分数.
4.分数的约分
约分:把一个分数化成同它相等,但分子、分母都比较小的分数,叫做约分.
约分的方法:一般用分子和分母的_______ (1除外)去除分数的分子和分母; 通常要除到得出最简分数为止.约分时,如果能很快看出分子和分母的最大 公约数,直接用它们的最大公约数去除比较简便.
公约数
1.分式的基本性质
分式的分子与分母同乘(或除以)一个 的整式,分式的值
学 前 温 故
.
答案:不等于0 不变
2.填空:(1) = ;(2) = .
答案:(1)a2 (2)x2+xy
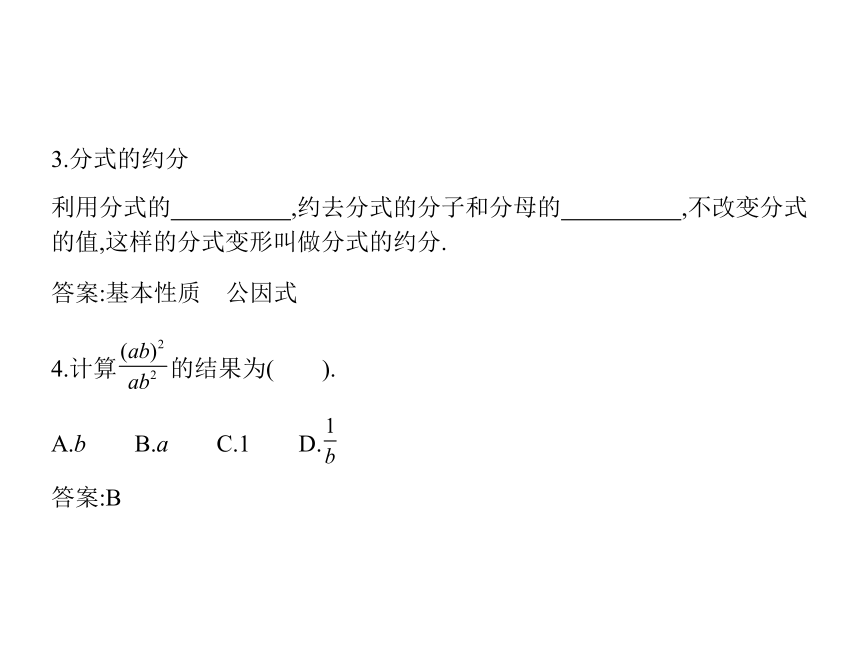
4.计算 的结果为( ).
3.分式的约分
利用分式的 ,约去分式的分子和分母的 ,不改变分式 的值,这样的分式变形叫做分式的约分.
答案:基本性质 公因式
A.b B.a C.1 D.
答案:B
5.最简分式
分子与分母没有 的分式,叫做最简分式.
答案:公因式
6.分式 , , 中最简分式有( ).
A.0个 B.1个 C.2个 D.3个
答案:B
8.最简公分母
为通分,要先确定各分式的公分母,一般取各分母的所有因式的最高次幂的 积作为公分母,它叫做 .
答案:最简公分母
9.下列分式: ,- , 的最简公分母是 .
答案:12a2b2c2
7.分式的通分
利用分式的 ,使分子和分母同乘适当的整式,不改变分式的值, 把几个分式化成相同分母的分式,这样的分式变形叫做分式的 .
答案:基本性质 通分
1.分式的约分
【例1】 约分:(1) ;(2) .
分析:(1)如果分式的分子、分母都是单项式,就直接约去分子、分母的公 因式,即分子、分母系数的最大公约数及相同字母的最低次幂;
(2)如果分子、分母都是多项式,就先分解因式,找出公因式,再进行约分.
解:(1) = =- .
(2) =- =- .
点拨:要牢记分子、分母都是乘积形式时,才能进行约分;约分要彻底,即约 去公因式后为最简形式.
2.分式的通分
【例2】 通分: , .
分析:应先把第二个分式的分母因式分解,再找最简公分母,然后再通分.
点拨:找最简公分母的方法:(1)系数:找各分母系数的最小公倍数;(2)字母因 式:找各分母中所有字母因式及其最高次幂;(3)多项式因式:先将多项式分 解因式,再取各分母中所有多项式因式及其最高次幂.它们的乘积即是最简 公分母.
解:最简公分母是6xy2(3+x)(3-x).
=
= ;
=
= .
1.等式 = 成立的条件是( ).
A.a≠0且b≠0 B.a≠1且b≠1
C.a≠-1且b≠-1 D.a,b为任意实数
答案:C
A.①② B.②④
C.③④ D.①②③④
解析:①和③中a,c可能为0;②和④中b和(-1-m2)均不为0.
答案:B
16.1.2 分式的基本性质
1.分数的基本性质
分数的分子和分母都乘(或除以)同一个________的数,分数的值不变.
2.分数的通分
把几个异分母的分数化为同分母的分数叫做分数的通分,最简公分母取各 个分母的______________.
学 前 温 故
不等于0
最小公倍数
3.最简分数
分子、分母是互质的分数,即分子和分母的最大公因数是1,这样的分数叫 做最简分数.
4.分数的约分
约分:把一个分数化成同它相等,但分子、分母都比较小的分数,叫做约分.
约分的方法:一般用分子和分母的_______ (1除外)去除分数的分子和分母; 通常要除到得出最简分数为止.约分时,如果能很快看出分子和分母的最大 公约数,直接用它们的最大公约数去除比较简便.
公约数
1.分式的基本性质
分式的分子与分母同乘(或除以)一个 的整式,分式的值
学 前 温 故
.
答案:不等于0 不变
2.填空:(1) = ;(2) = .
答案:(1)a2 (2)x2+xy
4.计算 的结果为( ).
3.分式的约分
利用分式的 ,约去分式的分子和分母的 ,不改变分式 的值,这样的分式变形叫做分式的约分.
答案:基本性质 公因式
A.b B.a C.1 D.
答案:B
5.最简分式
分子与分母没有 的分式,叫做最简分式.
答案:公因式
6.分式 , , 中最简分式有( ).
A.0个 B.1个 C.2个 D.3个
答案:B
8.最简公分母
为通分,要先确定各分式的公分母,一般取各分母的所有因式的最高次幂的 积作为公分母,它叫做 .
答案:最简公分母
9.下列分式: ,- , 的最简公分母是 .
答案:12a2b2c2
7.分式的通分
利用分式的 ,使分子和分母同乘适当的整式,不改变分式的值, 把几个分式化成相同分母的分式,这样的分式变形叫做分式的 .
答案:基本性质 通分
1.分式的约分
【例1】 约分:(1) ;(2) .
分析:(1)如果分式的分子、分母都是单项式,就直接约去分子、分母的公 因式,即分子、分母系数的最大公约数及相同字母的最低次幂;
(2)如果分子、分母都是多项式,就先分解因式,找出公因式,再进行约分.
解:(1) = =- .
(2) =- =- .
点拨:要牢记分子、分母都是乘积形式时,才能进行约分;约分要彻底,即约 去公因式后为最简形式.
2.分式的通分
【例2】 通分: , .
分析:应先把第二个分式的分母因式分解,再找最简公分母,然后再通分.
点拨:找最简公分母的方法:(1)系数:找各分母系数的最小公倍数;(2)字母因 式:找各分母中所有字母因式及其最高次幂;(3)多项式因式:先将多项式分 解因式,再取各分母中所有多项式因式及其最高次幂.它们的乘积即是最简 公分母.
解:最简公分母是6xy2(3+x)(3-x).
=
= ;
=
= .
1.等式 = 成立的条件是( ).
A.a≠0且b≠0 B.a≠1且b≠1
C.a≠-1且b≠-1 D.a,b为任意实数
答案:C
A.①② B.②④
C.③④ D.①②③④
解析:①和③中a,c可能为0;②和④中b和(-1-m2)均不为0.
答案:B
