有理数的乘方（二）教学设计

第二章 有理数及其运算
10．有理数的乘法（二）
太原五中 路丘平
学生起点分析：
学生的知识技能基础：学生在上一节课刚刚学习了有理数乘方的有关概念，法则等知识，对有理数乘方的符号表示，运算方法，符号判定比较熟悉，具备了进一步学习有理数乘方运算的知识技能基础，并且通过初中数学的学习，对运算数学知识解决实际问题有了一定的主动性，掌握了初步的估算方法，这对本节课的学习奠定了良好的基础.
学生的活动经验基础：较大的数据在报刊杂志上时常出现，而学生对此却缺乏经验，但是经过计算不难得出一张纸对折20次的厚度.将大数与身边熟悉的事物进行比较，从而得到启示，这个过程的实施，学生具有丰富的经验，比如折纸操作，测量厚度，估算高度，分析讨论，猜测验证等等，这对于本节课的学习非常有用.
学习任务分析：
教科书在学生掌握了有理数乘方的概念和运算的基础上，提出了本节课的具体学习任务；通过师生折纸的共同活动，体验当底数大于1时，乘方的运算结果增大的很快.并进一步熟练有理数乘方的运算的技能.本节课的教学目标是：
通过实例感受有理数的乘方运算，当底数大于1时，幂增大的很快.
熟练掌握有理数的乘方运算.
参与折纸操作数学活动，在具体的情境中初步掌握估算的方法，获得一些经险，为本册书第六章第一节“认识100万”的学习打基础.
教学过程设计
本节课设计了五个环节：第一环节：故事情境，引入新课；第二环节：折纸活动，计算思考；第三环节：例题练习，熟练乘方；第四环节：课堂小结；第五环节：布置作业.
第一环节：故事情境，引入新课
活动内容：
复习回顾
什么是有理数的乘方
求n个相同因数a的积的运算叫做乘方，乘方的结果叫做幂，a叫做底数，n叫做指数，an读作a的n次幂（或a的n次方）.
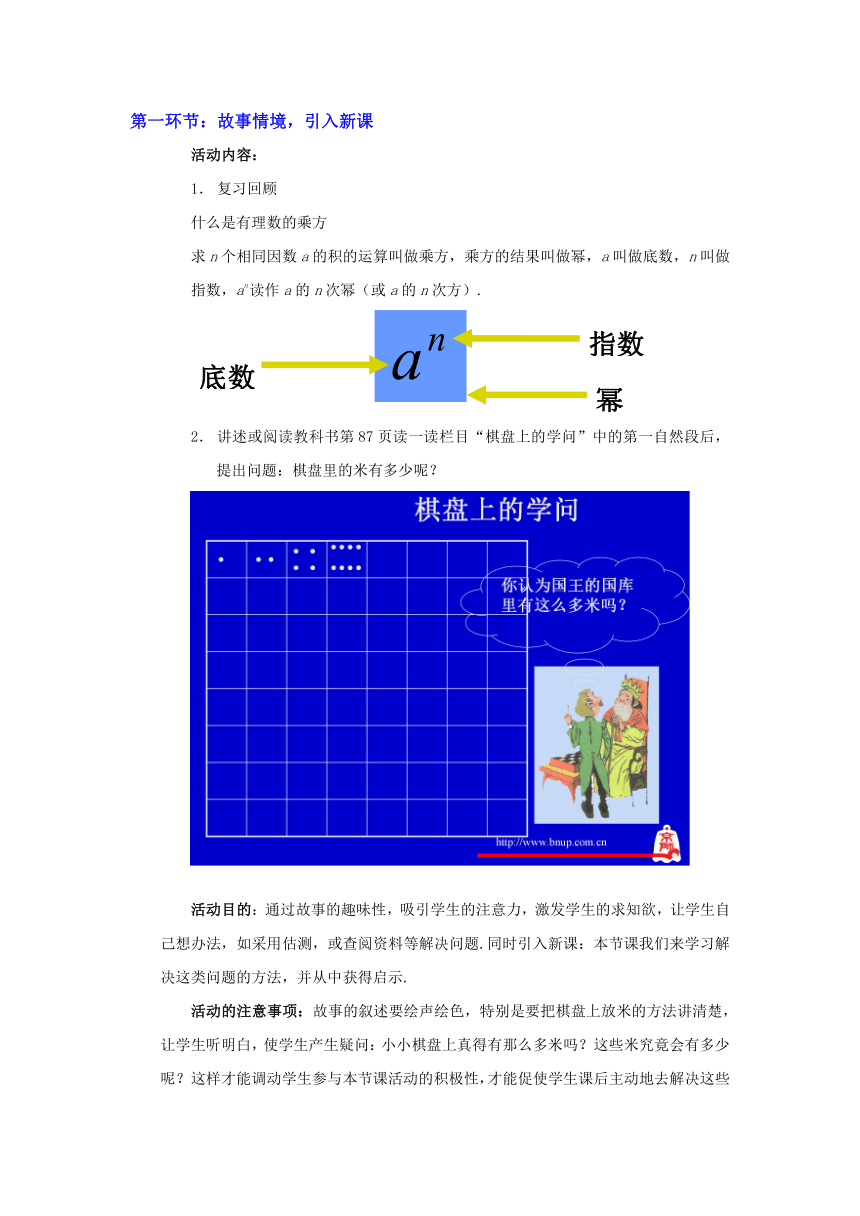
讲述或阅读教科书第87页读一读栏目“棋盘上的学问”中的第一自然段后，提出问题：棋盘里的米有多少呢？
活动目的：通过故事的趣味性，吸引学生的注意力，激发学生的求知欲，让学生自己想办法，如采用估测，或查阅资料等解决问题.同时引入新课：本节课我们来学习解决这类问题的方法，并从中获得启示.
活动的注意事项：故事的叙述要绘声绘色，特别是要把棋盘上放米的方法讲清楚，让学生听明白，使学生产生疑问：小小棋盘上真得有那么多米吗？这些米究竟会有多少呢？这样才能调动学生参与本节课活动的积极性，才能促使学生课后主动地去解决这些问题.
第二个环节：折纸活动，计算思考
活动内容：1.师生共同参与折纸活动，一边折，一边思考以下问题：纸的厚度为0.1mm ,对折一次后,厚度为2*0.1mm,对折两次后,厚度为多少毫米
对折20次后,厚度为多少毫米
若每层楼高度为3米,这张纸对折20次后约有多少层楼高
通过活动,你从中得到了什么启示
2.解决问题：
棋盘上的米究竟有多少
第2格有_______粒米,
第3格有_______粒米,
第4格有_______粒米,
… … … …
第64格有_______粒米，
共有_______粒米.
假设10000粒米为1斤，100斤为1袋，估计有-------袋
活动目的:培养学生积极参与课堂教学的意识,提高动手能力,猜想能力,估算能力.
加深对乘方意义的理解,进一步体会：当指数不断增加时,底数为2的幂的增长速度相当快；积累经验:当一张纸对折20次后,其厚度比30层楼还高,为本册第六章的学习打基础.
活动的注意事项：老师要与学生共同参与折纸活动，一起讨论，并尽可能利用上节细胞分裂的结果去发现一张纸对折10次后的厚度是1张纸的厚度的1024倍，可得102.4mm,对后10次的对折,应让学生先估算猜测后再计算验证,最后应提示学生去思考棋盘上的米究竟有多少 该如何去计算 或者建议学生去查阅有关资料.
第三环节：例题练习，熟悉乘方
活动内容：（1）讲解教科书第86页例3计算：
①-（-3）2；②-（-2）3；③-（-2/3）3；④-3/42.
（2）教科书第86页随堂练习1计算：
①-（3/2）2；②-（-3/2）2；③-53；④-4/32.
（3）巩固练习：
⒈ 填空
（1）310的意义是 个3相乘.
（2） 平方等于它本身的数是 .立方等于它本身的数是 .
（3） 一个数的15次幂是负数，那么这个数的2003次幂是 .
（4）(－2)6中指数是 ，底数是 .
（5）平方等于1/64的数是 ，立方等于1/64 的数是 .
2.计算：
⑴ (－1/3 )3 ； ⑵ －32×23； ⑶ (－3)2×(－2)3
⑷ －2×32； ⑸ (－2×3)2； ⑹ (－2)14×(－1/2)15；
⑺ －(－2)4; ⑻ (－1)2001； ⑼ －23＋(－3)2；
⑽ (－2)2 · (－3)2.
活动目的：例题讲解的目的一方面是进一步熟悉乘方运算，另一方面是为了区分一些易于混淆的表示法，例如-32、（-3）2、-（-3）2 它们意义不同，-32表示32的相反数，底数是3；（-3）2的底数是-3；-（-3）2表示（-3）2的相反数，底数是-3；（-2/3）3与-22/3有区别：（-2/3）3的底数是-2/3，是乘方运算，而-23/3的分子是乘方运算，底数是2，整体是混合运算，随堂练习的目的是巩固课堂知识，是例题讲解的继续.
活动的注意事项：例题讲解要先分析，再计算，要把每一个题的读法及含义分析透彻.
讲明运算顺序和运算依据，再板书格式，另外要特别强调.在乘方运算中，当底数是负数或分数时，一定要把整个负数或分数用小括号括起来.随堂练习的题目与例题相类似，要引导学生认真计算，及时纠正学生在计算中出现的错误，并明确错误的原因，掌握算理.这里要特别注意，不要补充不必要的繁难计算题.
第四环节：课堂小结
活动内容：请同学们谈一下本节课的收获和感想.
1.乘方的意义
2.当底数大于1时，乘方运算的结果增长得很快
3 .乘方的运算
活动目的：提高学生的课堂参与意识，发展学生的课堂小节能力，语言表达交流能力.为学生提供展示自我，凸显个性的机会.
活动的注意事项：教师一方面应积极鼓励学生参与，特别是为学习有困难的学生创设发言机会，以提高他们的兴趣和自信，另一方面要把握课堂小结的准确性和全面性，对学生的小节做出适当的补充和修正.
第五环节：布置作业
活动内容：教科书第87页习题2.14 知识技能1计算,问题解决1.
活动目的：复习巩固检测本节知识，训练提高运算技能和解决问题的能力.
活动注意事项：对知识技能1计算，要向学生明确提出书写要求，即不能直接写结果，而要把演算步骤过程写出来并明确算理，对问题解决1应让学生由此感受到当底数小于1时，乘方运算的结果减少的速度很快.
教学反思
本节课的教学可不必拘泥于教科书的设计，可以创造性地使用教材，例如可把折纸活动设计成猜一猜，让学生先凭借以往的经验和知识进行猜测，以激发学生的求知欲，极大地调动学生学习的积极性，然后再指导学生用实践来验证，通过动手折纸找规律，寻找结论.
例题的讲解和分析也可以让学生先去做，在做的过程中发现问题，再着手解决问题，当学生做题产生了不同的答案后，教师再来分析错误的原因，并让学生经历了错误过程的同时又经历了改正错误的过程，印象应该更深刻.
本节课题的引入若能配上栩栩如生的动画，把学生吸引到数学王国中，激发学生的兴趣效果会更好.
底数
指数
幂