7.1几种常见的几何体教案
图片预览

文档简介
阿城中学教案
科目:数学 年级:九年级下 主备人:魏方红 授课人:王秀焕
第 8 课时 备课时间 2012.2.21 授课时间 2012.2.22
课题 7.1几种常见的几何体
教学目 标 经历从现实世界抽象出几何图形的过程,体会丰富多彩的图形世界。了解几何体、多面体、平面图形的意义。通过对平面图形的组合设计渗透知识来源于实践并应用于实践的思想,激发学生的学习兴趣。
教学重点: 多面体及其有关概念。
教学难点: 在具体的问题情境中识别多面体及其有关概念,如面、棱、顶点。
课型: 新授课 教 具 课件
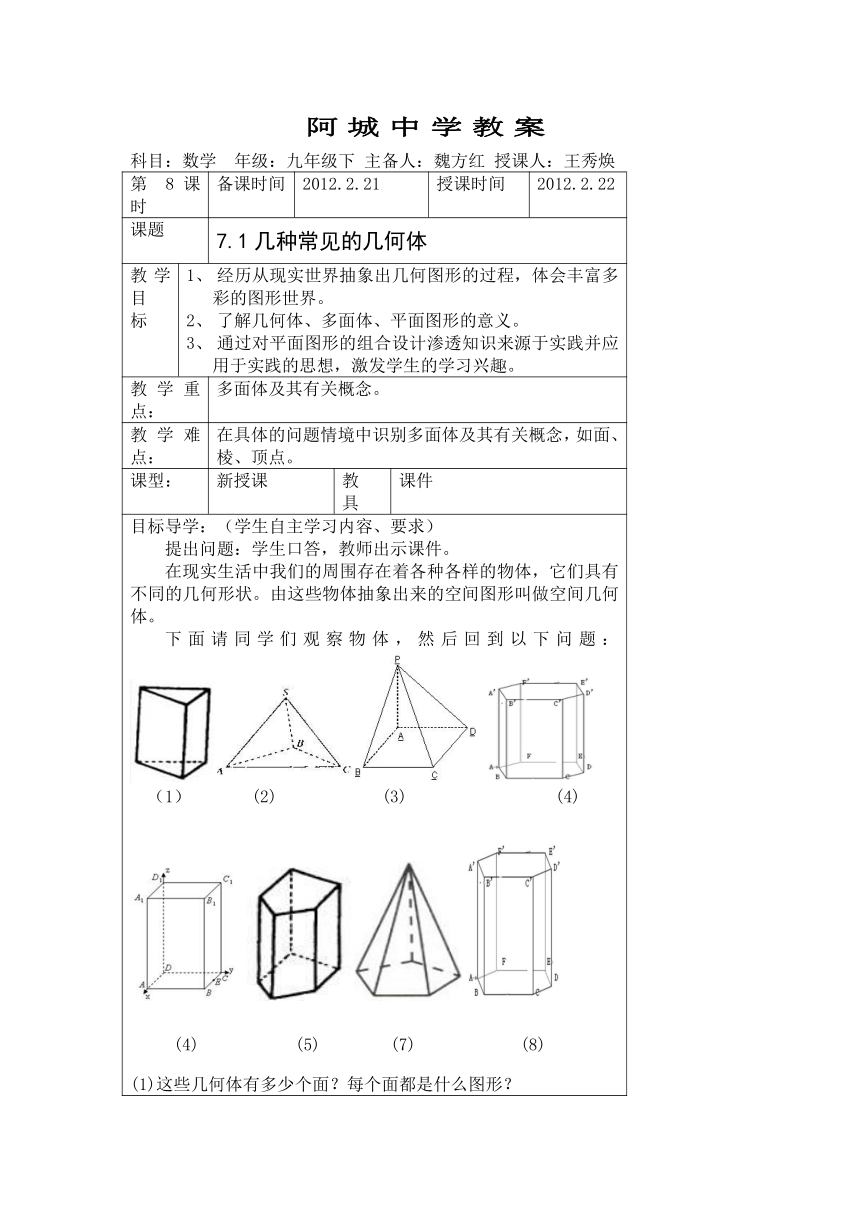
目标导学:(学生自主学习内容、要求)提出问题:学生口答,教师出示课件。在现实生活中我们的周围存在着各种各样的物体,它们具有不同的几何形状。由这些物体抽象出来的空间图形叫做空间几何体。下面请同学们观察物体,然后回到以下问题:(1) (2) (3) (4) (4) (5) (7) (8)(1)这些几何体有多少个面?每个面都是什么图形?(2)这些几何体是由什么图形围成的?(3)这些几何体可以分成几类?像这样由多边形围成的几何体,叫做多面体。围成多面体的多边形的边叫做多面体的棱,多边形的顶点叫做多面体的顶点。
学生自主学习小组讨论(提问问题、导学探究讨论内容、方式等)引导学生观察、总结:棱柱的结构特征定义:有连个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。棱柱的有关概念:棱柱中,两个互相平行的面叫做棱柱的底面(简称底),其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点。棱柱的分类:按底面多边形的边数分,有三棱柱、四棱柱、五棱柱等。棱锥的结构特征定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。棱锥的有关概念:棱锥中,这个多边形面叫做棱锥的底面或底,有公共顶点各个三角形的面叫做棱锥的侧面,各侧面的公共顶点 叫做棱锥的顶点,相邻侧面的公共边叫做棱锥的侧棱。 (3)棱锥的分类:按底面的多边形的边数分,有三棱锥、四棱锥、五棱锥等。
交流展示(内容、方式、过程等)讨论:棱柱、棱锥分别具有一些什么几何性质?有什么共同的性质?学生小组内交流、讨论,观察几何体,并说出它们的共同特点。在讨论后,让学生总结出共同的性质。棱台的结构特征:棱台的概念:棱锥被平行于棱锥底面的平面所截后,截面和底面之间的部分叫做棱台。分类:三棱台、四棱台、五棱台。特点:两个底面是相似多边形,侧面都是梯形;侧棱延长后交于一点。出示下面几何体是多面体吗?为什么?它们有什么共同特点?学生观察后,总结:围成它们的面不是多边形,所以不是多面体。它们都有一个面是曲面。你过去学过哪些几何体的表面积公式和体积公式?你能用字母将它们分别表示出来吗?学生在练习本上写一写,交流订正。出示例1:用8个冷场都为a的立方体,组合成一个长方体。有哪几种不同的组合方式?按那种方式组合,组合成的长方体表面积最小?学生小组内讨论交流后,独立完成,指名上台板演,教师巡视指导,最后集体订正。6、“挑战自我”请你说出煤精组印中有多少条棱,多少个顶点吗?与同学交流。
归纳总结(教师总结、释难解疑及师生互动探究) 强调,点拨:多面体是由多个平面多边形组成的,切记是“平面多边形”。棱柱、棱锥和棱台有各自的不同,要把所学的几何体的图形想象在脑子中,在解题时,灵活应用。
练习反馈:1、下列图形中有14条棱的是 ( ) A、四棱柱 B、四棱锥 C、圆柱 D、四棱柱切去一个角2、一个多面体有10条棱,6个顶点,则这个多面体是( )体。3、长方体有( )个顶点,经过每个顶点有( )条棱,共有( )条棱。4、一个七棱柱共有( )个面,( )条棱,( )个顶点。作业:习题7.1中A组的第1题。
板书设计:7.1 几种常见的几何体1、多面体的定义 例1::2、棱柱定义3、棱锥定义4、棱台定义5、多面体的面,多面体的棱,多面体的顶点
课后反思:
科目:数学 年级:九年级下 主备人:魏方红 授课人:王秀焕
第 8 课时 备课时间 2012.2.21 授课时间 2012.2.22
课题 7.1几种常见的几何体
教学目 标 经历从现实世界抽象出几何图形的过程,体会丰富多彩的图形世界。了解几何体、多面体、平面图形的意义。通过对平面图形的组合设计渗透知识来源于实践并应用于实践的思想,激发学生的学习兴趣。
教学重点: 多面体及其有关概念。
教学难点: 在具体的问题情境中识别多面体及其有关概念,如面、棱、顶点。
课型: 新授课 教 具 课件
目标导学:(学生自主学习内容、要求)提出问题:学生口答,教师出示课件。在现实生活中我们的周围存在着各种各样的物体,它们具有不同的几何形状。由这些物体抽象出来的空间图形叫做空间几何体。下面请同学们观察物体,然后回到以下问题:(1) (2) (3) (4) (4) (5) (7) (8)(1)这些几何体有多少个面?每个面都是什么图形?(2)这些几何体是由什么图形围成的?(3)这些几何体可以分成几类?像这样由多边形围成的几何体,叫做多面体。围成多面体的多边形的边叫做多面体的棱,多边形的顶点叫做多面体的顶点。
学生自主学习小组讨论(提问问题、导学探究讨论内容、方式等)引导学生观察、总结:棱柱的结构特征定义:有连个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。棱柱的有关概念:棱柱中,两个互相平行的面叫做棱柱的底面(简称底),其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点。棱柱的分类:按底面多边形的边数分,有三棱柱、四棱柱、五棱柱等。棱锥的结构特征定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。棱锥的有关概念:棱锥中,这个多边形面叫做棱锥的底面或底,有公共顶点各个三角形的面叫做棱锥的侧面,各侧面的公共顶点 叫做棱锥的顶点,相邻侧面的公共边叫做棱锥的侧棱。 (3)棱锥的分类:按底面的多边形的边数分,有三棱锥、四棱锥、五棱锥等。
交流展示(内容、方式、过程等)讨论:棱柱、棱锥分别具有一些什么几何性质?有什么共同的性质?学生小组内交流、讨论,观察几何体,并说出它们的共同特点。在讨论后,让学生总结出共同的性质。棱台的结构特征:棱台的概念:棱锥被平行于棱锥底面的平面所截后,截面和底面之间的部分叫做棱台。分类:三棱台、四棱台、五棱台。特点:两个底面是相似多边形,侧面都是梯形;侧棱延长后交于一点。出示下面几何体是多面体吗?为什么?它们有什么共同特点?学生观察后,总结:围成它们的面不是多边形,所以不是多面体。它们都有一个面是曲面。你过去学过哪些几何体的表面积公式和体积公式?你能用字母将它们分别表示出来吗?学生在练习本上写一写,交流订正。出示例1:用8个冷场都为a的立方体,组合成一个长方体。有哪几种不同的组合方式?按那种方式组合,组合成的长方体表面积最小?学生小组内讨论交流后,独立完成,指名上台板演,教师巡视指导,最后集体订正。6、“挑战自我”请你说出煤精组印中有多少条棱,多少个顶点吗?与同学交流。
归纳总结(教师总结、释难解疑及师生互动探究) 强调,点拨:多面体是由多个平面多边形组成的,切记是“平面多边形”。棱柱、棱锥和棱台有各自的不同,要把所学的几何体的图形想象在脑子中,在解题时,灵活应用。
练习反馈:1、下列图形中有14条棱的是 ( ) A、四棱柱 B、四棱锥 C、圆柱 D、四棱柱切去一个角2、一个多面体有10条棱,6个顶点,则这个多面体是( )体。3、长方体有( )个顶点,经过每个顶点有( )条棱,共有( )条棱。4、一个七棱柱共有( )个面,( )条棱,( )个顶点。作业:习题7.1中A组的第1题。
板书设计:7.1 几种常见的几何体1、多面体的定义 例1::2、棱柱定义3、棱锥定义4、棱台定义5、多面体的面,多面体的棱,多面体的顶点
课后反思:
