2.3气体的等压和等容变化 —2020-2021学年【新教材】人教版(2019)高中物理选择性必修三课件14张PPT
文档属性
| 名称 | 2.3气体的等压和等容变化 —2020-2021学年【新教材】人教版(2019)高中物理选择性必修三课件14张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 782.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-21 07:35:34 | ||
图片预览




文档简介
物理选择性必修3
第二章
气体液体和固体
气体的等压和等容变化
3
一 气体的等压变化
1.气体的等压变化:
一定质量的某种气体,在压强不变时,体积随温度变化的过程。
2.盖—吕萨克定律
一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
(1)内容:
(2)表达式:
t
O
V
-273.15
(3)图像:等压曲线
p1V=CT(其中C是常量),或 或 。
同一条直线上压强相同
p1
T
O
V
p2
③压强越大,斜率越小。如图2:p1>p2>p3>p4。
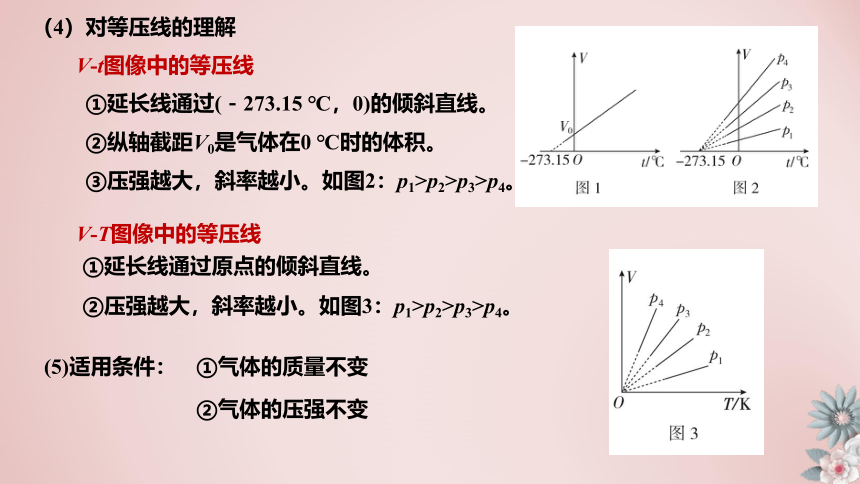
(4)对等压线的理解
V?t图像中的等压线
①延长线通过(-273.15 ℃,0)的倾斜直线。
②纵轴截距V0是气体在0 ℃时的体积。
V?T图像中的等压线
①延长线通过原点的倾斜直线。
②压强越大,斜率越小。如图3:p1>p2>p3>p4。
(5)适用条件:
①气体的质量不变
②气体的压强不变
二 气体的等容变化
一定质量的某种气体,在体积不变时,压强随温度变化的过程。
1.气体的等容变化:
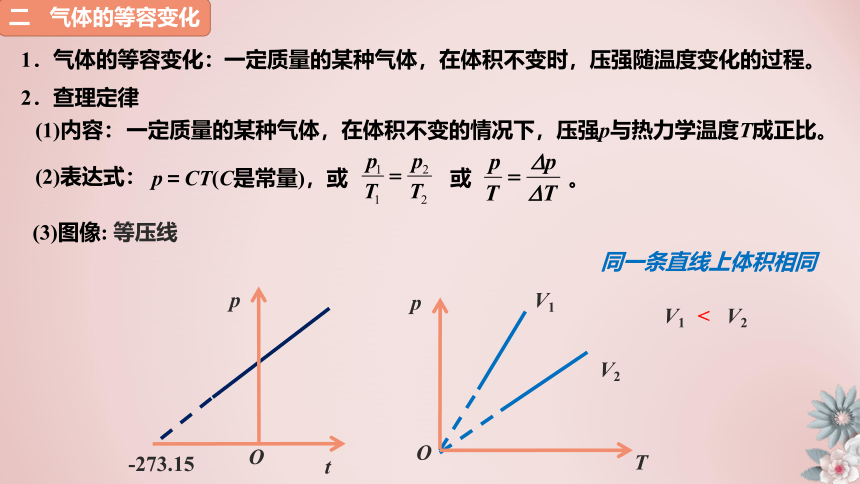
2.查理定律
(1)内容:
一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比。
(2)表达式:
p=CT(C是常量),或 或 。
(3)图像: 等压线
同一条直线上体积相同
V1 V2
<
t
O
p
-273.15
V1
T
O
p
V2
③体积越大,斜率越小。如图2:V1>V2>V3>V4。
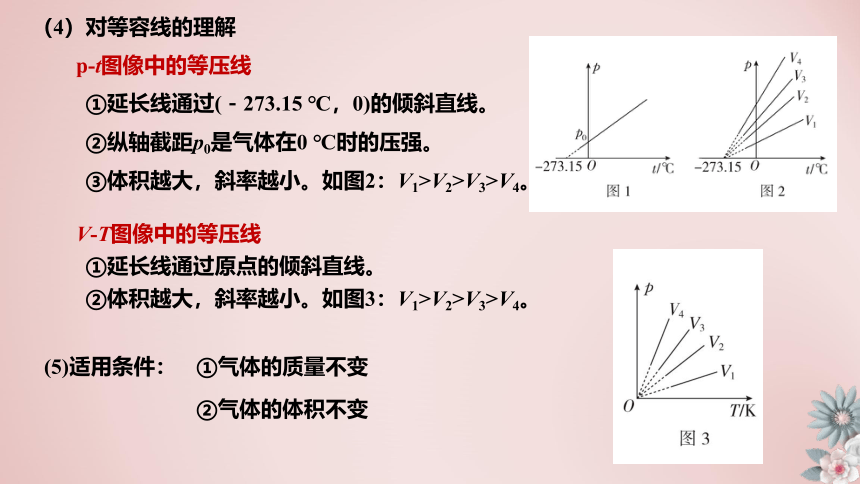
(4)对等容线的理解
p?t图像中的等压线
①延长线通过(-273.15 ℃,0)的倾斜直线。
②纵轴截距p0是气体在0 ℃时的压强。
V?T图像中的等压线
①延长线通过原点的倾斜直线。
②体积越大,斜率越小。如图3:V1>V2>V3>V4。
(5)适用条件:
①气体的质量不变
②气体的体积不变
描述气体状态的三个参量:
T不变,p、V变化:玻意耳定律
V不变,p、T变化:查理定律
p不变,V、T变化:盖-吕萨克定律
若,p、V、T 都变化,会遵循什么样的规律?
适用条件:压强不太大,温度不太低
p、V、T
某种气体的压强为2×105Pa,体积为1m3,温度为200K。它经过等温过程后体积变为2m3。随后,又经过等容变化,温度变为300K,求此时气体的压强.
例题
解:
根据查理定律,有
状态1:p1=2×105Pa,V1=1m3,T1=200K
根据玻意耳定律,有p1V1=p2V2
等温后状态2:p2=?,V2=2m3,T2=200K
等容后状态3:p3=?,V3=2m3,T3=300K
可得
可得
T1=T2
V1=V2
三 理想气体
1.定义:
在任何温度、任何压强下都严格遵从气体实验定律的气体。
2、理解:
1)理想气体是种理想化模型.
实际气体,在压强不太大,温度不太低时,可以近似看成理想气体。
2)
理想气体,忽略分子间势能,内能等于分子的总动能。
3)
四 理想气体状态方程
1、一定质量的理想气体,由初状态(p1、V1、T1)变化到末状态(p2、V2、T2)时,各量满足 .
上面两式都叫一定质量的理想气体状态方程。
2、说明
一定质量的某种理想气体.
2)适用条件:
1) 式中C与p、V、T无关,只与气体的种类和质量有关.
3 )该方程表示的是p、V、T的关系,与中间的变化过程无关。
①当T1=T2时,p1V1=p2V2 (玻意耳定律)
②当V1=V2时, (查理定律)
③当 p1=p2时, (盖-铝萨克定律)
3)气体的三个实验定律是理想气体状态方程的特例:
3.理想气体状态方程的应用
(1)解题步骤
①确定研究对象,即某一定质量的理想气体,分析它的变化过程;
②确定初、末两状态,准确找出初、末两状态的六个状态参量,特别是压强;
③用理想气体状态方程列式,并求解。
(2)注意:
①气体质量保持不变
②T必须是热力学温度,公式两边p和V单位统一,可不是国际单位。
五 气体实验定律的微观解释
1、玻意耳定律:
一定质量的某种理想气体,温度保持不变时,分子的平均动能是一定的。在这种情况下,体积减小时,分子的分子密集程度增大,气体的压强就增大。
3、查理定律:
一定质量的某种理想气体,体积保持不变时,分子的密集程度保持不变。在这种情况下,温度升高时,分子的平均动能增大,气体的压强就增大。
2、盖-吕萨克定律:
一定质量的某种理想气体,温度升高时,分子的平均动能增大;只有气体的体积同时增大,使分子的密集程度减少,才能保持压强不变。
T 不变
V 不变
p 不变
课堂小结
一、气体等压变化,
二、气体等容变化
三、理想气体状态方程
1、三个实验定律是理想气体状态方程的特例
2、适用条件
3、应用步骤
感谢聆听
第二章
气体液体和固体
气体的等压和等容变化
3
一 气体的等压变化
1.气体的等压变化:
一定质量的某种气体,在压强不变时,体积随温度变化的过程。
2.盖—吕萨克定律
一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
(1)内容:
(2)表达式:
t
O
V
-273.15
(3)图像:等压曲线
p1
同一条直线上压强相同
p1
T
O
V
p2
③压强越大,斜率越小。如图2:p1>p2>p3>p4。
(4)对等压线的理解
V?t图像中的等压线
①延长线通过(-273.15 ℃,0)的倾斜直线。
②纵轴截距V0是气体在0 ℃时的体积。
V?T图像中的等压线
①延长线通过原点的倾斜直线。
②压强越大,斜率越小。如图3:p1>p2>p3>p4。
(5)适用条件:
①气体的质量不变
②气体的压强不变
二 气体的等容变化
一定质量的某种气体,在体积不变时,压强随温度变化的过程。
1.气体的等容变化:
2.查理定律
(1)内容:
一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比。
(2)表达式:
p=CT(C是常量),或 或 。
(3)图像: 等压线
同一条直线上体积相同
V1 V2
<
t
O
p
-273.15
V1
T
O
p
V2
③体积越大,斜率越小。如图2:V1>V2>V3>V4。
(4)对等容线的理解
p?t图像中的等压线
①延长线通过(-273.15 ℃,0)的倾斜直线。
②纵轴截距p0是气体在0 ℃时的压强。
V?T图像中的等压线
①延长线通过原点的倾斜直线。
②体积越大,斜率越小。如图3:V1>V2>V3>V4。
(5)适用条件:
①气体的质量不变
②气体的体积不变
描述气体状态的三个参量:
T不变,p、V变化:玻意耳定律
V不变,p、T变化:查理定律
p不变,V、T变化:盖-吕萨克定律
若,p、V、T 都变化,会遵循什么样的规律?
适用条件:压强不太大,温度不太低
p、V、T
某种气体的压强为2×105Pa,体积为1m3,温度为200K。它经过等温过程后体积变为2m3。随后,又经过等容变化,温度变为300K,求此时气体的压强.
例题
解:
根据查理定律,有
状态1:p1=2×105Pa,V1=1m3,T1=200K
根据玻意耳定律,有p1V1=p2V2
等温后状态2:p2=?,V2=2m3,T2=200K
等容后状态3:p3=?,V3=2m3,T3=300K
可得
可得
T1=T2
V1=V2
三 理想气体
1.定义:
在任何温度、任何压强下都严格遵从气体实验定律的气体。
2、理解:
1)理想气体是种理想化模型.
实际气体,在压强不太大,温度不太低时,可以近似看成理想气体。
2)
理想气体,忽略分子间势能,内能等于分子的总动能。
3)
四 理想气体状态方程
1、一定质量的理想气体,由初状态(p1、V1、T1)变化到末状态(p2、V2、T2)时,各量满足 .
上面两式都叫一定质量的理想气体状态方程。
2、说明
一定质量的某种理想气体.
2)适用条件:
1) 式中C与p、V、T无关,只与气体的种类和质量有关.
3 )该方程表示的是p、V、T的关系,与中间的变化过程无关。
①当T1=T2时,p1V1=p2V2 (玻意耳定律)
②当V1=V2时, (查理定律)
③当 p1=p2时, (盖-铝萨克定律)
3)气体的三个实验定律是理想气体状态方程的特例:
3.理想气体状态方程的应用
(1)解题步骤
①确定研究对象,即某一定质量的理想气体,分析它的变化过程;
②确定初、末两状态,准确找出初、末两状态的六个状态参量,特别是压强;
③用理想气体状态方程列式,并求解。
(2)注意:
①气体质量保持不变
②T必须是热力学温度,公式两边p和V单位统一,可不是国际单位。
五 气体实验定律的微观解释
1、玻意耳定律:
一定质量的某种理想气体,温度保持不变时,分子的平均动能是一定的。在这种情况下,体积减小时,分子的分子密集程度增大,气体的压强就增大。
3、查理定律:
一定质量的某种理想气体,体积保持不变时,分子的密集程度保持不变。在这种情况下,温度升高时,分子的平均动能增大,气体的压强就增大。
2、盖-吕萨克定律:
一定质量的某种理想气体,温度升高时,分子的平均动能增大;只有气体的体积同时增大,使分子的密集程度减少,才能保持压强不变。
T 不变
V 不变
p 不变
课堂小结
一、气体等压变化,
二、气体等容变化
三、理想气体状态方程
1、三个实验定律是理想气体状态方程的特例
2、适用条件
3、应用步骤
感谢聆听
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
