19.2.3《正方形》课件(人教版八年级下)
文档属性
| 名称 | 19.2.3《正方形》课件(人教版八年级下) |  | |
| 格式 | zip | ||
| 文件大小 | 290.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-28 22:10:41 | ||
图片预览








文档简介
(共26张PPT)
19.2.3 正方形
1.有一个角是直角的平行四边形是____.
学 前 温 故
2.邻边相等的平行四边形是____.
3.矩形的对角线________________.
4.菱形的对角线_______________.
矩形
菱形
相等且互相平分
垂直且互相平分
1.正方形的性质以及与矩形、菱形性质的比较
新 课 早 知
矩形 它们都具有平行四边形的性质:对边平行且相等对角相等对角线互相平分都是中心对称图形 角:四个角都是直角对角线:相等
菱形 边:四条边都相等对角线:互相垂直,每条对角线平分一组对角
正方形 边:四条边都相等角:四个角都是直角
对角线:相等且互相垂直,每条对角线平分一组对角
性质
共同性质 特殊性质
2.下列四边形:①正方形,②矩形,③菱形,对角线一定相等的是( ).
A.①②③ B.①② C.①③ D.②③
答案:B
3.正方形的判定
(1)邻边 的矩形是正方形;
(2)有一个角是 的菱形是正方形.
答案:(1)相等 (2)直角
4.下列命题中的假命题是( ).
A.一组邻边相等的平行四边形是菱形
B.一组邻边相等的矩形是正方形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等且有一个角是直角的四边形是矩形
答案:D
5.正方形的两条对角线把这个正方形分成 个全等的等腰 直角三角形.
答案:四
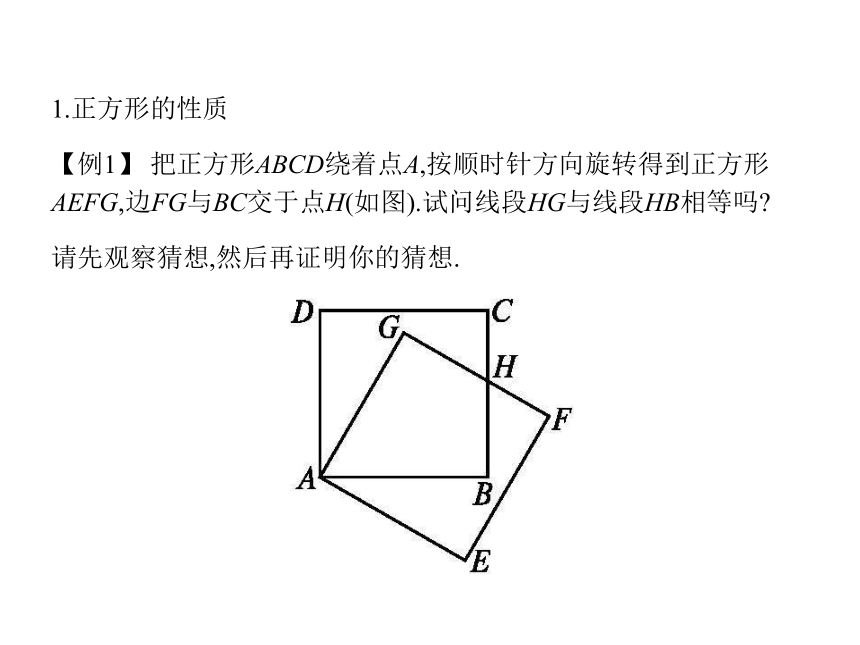
1.正方形的性质
【例1】 把正方形ABCD绕着点A,按顺时针方向旋转得到正方形 AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗
请先观察猜想,然后再证明你的猜想.
解:HG=HB.
证法一:连接AH,如图(1).
∵四边形ABCD,AEFG都是正方形,
∴∠B=∠G=90°.
由题意知AG=AB,又AH=AH,
∴Rt△AGH≌Rt△ABH.(HL)
∴HG=HB.
(1)
(2)
证法二:连接GB,如图(2).
∵四边形ABCD,AEFG都是正方形,
∴∠ABC=∠AGF=90°.
由题意知AB=AG.
∴∠AGB=∠ABG.
∴∠HGB=∠HBG.
∴HG=HB.
点拨:旋转前后的图形是全等形,正方形旋转前后的对应边相等.在寻 找等量关系时,通常添加辅助线,构造出全等三角形.
2.正方形的判定
【例2】 如图(1),在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA 上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
(1)如图(2),连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你 的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图 (3)的方式拼接成一个四边形.若正方形ABCD的边长为3 cm,HA=EB
=FC=GD=1 cm,则图(3)中阴影部分的面积为 cm2.
解:(1)四边形EFGH是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA.
∵HA=EB=FC=GD,
∴AE=BF=CG=DH.
∴△AEH≌△BFE≌△CGF≌△DHG.
∴EF=FG=GH=HE.
∴四边形EFGH是菱形.
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°.
∴∠GHE=90°.
∴四边形EFGH是正方形.
(2)1
点拨:证明一个四边形是正方形,一般应先证明它是一个菱形或矩形, 再证明它是正方形.
由△DHG≌△AEH知∠DHG=∠AEH.
1.如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个 正方形,剪刀与折痕所成的角的度数应为( ).
A.60° B.30° C.45° D.90°
答案:C
2.正方形内有一点A,到各边的距离从小到大依次是1,2,3,4,则正方形 的周长是( ).
A.10 B.20 C.24 D.25
解析:根据已知可得正方形的边长是5,
所以周长是20.
答案:B
3.如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点 E,且四边形ABCD的面积为8,则BE等于( ).
A.2 B.3
C.2 或 D.2 或
解析:过点B作BF⊥CD,交DC的延长线于点F,
可证△ABE≌△CBF,四边形EBFD为正方形,S四边形ABCD=S四边形EBFD=8,
∴BE=2 或 .
答案:C
4.如图,菱形ABCD的对角线相交于点O,请你添加一个条件: ,使得该菱形为正方形.
答案:答案不唯一,如AB⊥BC或AC=BD或AO=BO等
5.如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③ ④四个三角形的周长之和为 .
答案:32
6.(2011·广东肇庆中考)如图,在正方形ABCD中,E为对角线AC上一 点,连接EB、ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,若∠DEB=140°,求∠AFE的度数.
(1)证明:∵四边形ABCD是正方形,∴CD=CB.
∵AC是正方形的对角线,
∴∠DCA=∠BCA.
又CE=CE,∴△BEC≌△DEC.
(2)解:∵∠DEB=140°,
由△BEC≌△DEC可得∠DEC=∠BEC=140°÷2=70°.
∴∠AEF=∠BEC=70°.
又∵AC是正方形的对角线,∠DAB=90°,
∴∠DAC=∠BAC=90°÷2=45°.
在△AEF中,∠AFE=180°-70°-45°=65°.
7.如图,已知在△ABC中,∠ACB=90°,CD是∠ACB的平分线,DE∥AC 交BC于E,DF∥BC交AC于F.
求证:四边形CEDF是正方形.
证明:∵DE∥AC,DF∥BC,
∴四边形CEDF是平行四边形.
又∵∠ACB=90°,
∴ CEDF是矩形.
∴∠DEC=∠DFC=90°.
又∵CD是∠ACB的平分线,
∴DE=DF.∴矩形CEDF为正方形.
19.2.3 正方形
1.有一个角是直角的平行四边形是____.
学 前 温 故
2.邻边相等的平行四边形是____.
3.矩形的对角线________________.
4.菱形的对角线_______________.
矩形
菱形
相等且互相平分
垂直且互相平分
1.正方形的性质以及与矩形、菱形性质的比较
新 课 早 知
矩形 它们都具有平行四边形的性质:对边平行且相等对角相等对角线互相平分都是中心对称图形 角:四个角都是直角对角线:相等
菱形 边:四条边都相等对角线:互相垂直,每条对角线平分一组对角
正方形 边:四条边都相等角:四个角都是直角
对角线:相等且互相垂直,每条对角线平分一组对角
性质
共同性质 特殊性质
2.下列四边形:①正方形,②矩形,③菱形,对角线一定相等的是( ).
A.①②③ B.①② C.①③ D.②③
答案:B
3.正方形的判定
(1)邻边 的矩形是正方形;
(2)有一个角是 的菱形是正方形.
答案:(1)相等 (2)直角
4.下列命题中的假命题是( ).
A.一组邻边相等的平行四边形是菱形
B.一组邻边相等的矩形是正方形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等且有一个角是直角的四边形是矩形
答案:D
5.正方形的两条对角线把这个正方形分成 个全等的等腰 直角三角形.
答案:四
1.正方形的性质
【例1】 把正方形ABCD绕着点A,按顺时针方向旋转得到正方形 AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗
请先观察猜想,然后再证明你的猜想.
解:HG=HB.
证法一:连接AH,如图(1).
∵四边形ABCD,AEFG都是正方形,
∴∠B=∠G=90°.
由题意知AG=AB,又AH=AH,
∴Rt△AGH≌Rt△ABH.(HL)
∴HG=HB.
(1)
(2)
证法二:连接GB,如图(2).
∵四边形ABCD,AEFG都是正方形,
∴∠ABC=∠AGF=90°.
由题意知AB=AG.
∴∠AGB=∠ABG.
∴∠HGB=∠HBG.
∴HG=HB.
点拨:旋转前后的图形是全等形,正方形旋转前后的对应边相等.在寻 找等量关系时,通常添加辅助线,构造出全等三角形.
2.正方形的判定
【例2】 如图(1),在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA 上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
(1)如图(2),连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你 的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图 (3)的方式拼接成一个四边形.若正方形ABCD的边长为3 cm,HA=EB
=FC=GD=1 cm,则图(3)中阴影部分的面积为 cm2.
解:(1)四边形EFGH是正方形.
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA.
∵HA=EB=FC=GD,
∴AE=BF=CG=DH.
∴△AEH≌△BFE≌△CGF≌△DHG.
∴EF=FG=GH=HE.
∴四边形EFGH是菱形.
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°.
∴∠GHE=90°.
∴四边形EFGH是正方形.
(2)1
点拨:证明一个四边形是正方形,一般应先证明它是一个菱形或矩形, 再证明它是正方形.
由△DHG≌△AEH知∠DHG=∠AEH.
1.如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个 正方形,剪刀与折痕所成的角的度数应为( ).
A.60° B.30° C.45° D.90°
答案:C
2.正方形内有一点A,到各边的距离从小到大依次是1,2,3,4,则正方形 的周长是( ).
A.10 B.20 C.24 D.25
解析:根据已知可得正方形的边长是5,
所以周长是20.
答案:B
3.如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点 E,且四边形ABCD的面积为8,则BE等于( ).
A.2 B.3
C.2 或 D.2 或
解析:过点B作BF⊥CD,交DC的延长线于点F,
可证△ABE≌△CBF,四边形EBFD为正方形,S四边形ABCD=S四边形EBFD=8,
∴BE=2 或 .
答案:C
4.如图,菱形ABCD的对角线相交于点O,请你添加一个条件: ,使得该菱形为正方形.
答案:答案不唯一,如AB⊥BC或AC=BD或AO=BO等
5.如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③ ④四个三角形的周长之和为 .
答案:32
6.(2011·广东肇庆中考)如图,在正方形ABCD中,E为对角线AC上一 点,连接EB、ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,若∠DEB=140°,求∠AFE的度数.
(1)证明:∵四边形ABCD是正方形,∴CD=CB.
∵AC是正方形的对角线,
∴∠DCA=∠BCA.
又CE=CE,∴△BEC≌△DEC.
(2)解:∵∠DEB=140°,
由△BEC≌△DEC可得∠DEC=∠BEC=140°÷2=70°.
∴∠AEF=∠BEC=70°.
又∵AC是正方形的对角线,∠DAB=90°,
∴∠DAC=∠BAC=90°÷2=45°.
在△AEF中,∠AFE=180°-70°-45°=65°.
7.如图,已知在△ABC中,∠ACB=90°,CD是∠ACB的平分线,DE∥AC 交BC于E,DF∥BC交AC于F.
求证:四边形CEDF是正方形.
证明:∵DE∥AC,DF∥BC,
∴四边形CEDF是平行四边形.
又∵∠ACB=90°,
∴ CEDF是矩形.
∴∠DEC=∠DFC=90°.
又∵CD是∠ACB的平分线,
∴DE=DF.∴矩形CEDF为正方形.
