第1讲 一次函数与反比例函数 知识回顾+专题讲解+巩固练习-2021年中考数学二轮复习讲义(word版含答案)
文档属性
| 名称 | 第1讲 一次函数与反比例函数 知识回顾+专题讲解+巩固练习-2021年中考数学二轮复习讲义(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 877.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 05:42:28 | ||
图片预览




文档简介
第一讲一次函数与反比例函数
㈠承上启下 知识回顾
函数基础知识
(1)函数:如果在一个变化过程中,有两个变量x、y,对于x的每一个确定的值 ,y都有 唯一确定的值 与之对应,此时称y是x的 函数,其中x是自变量,y是因变量.
(2)自变量的取值范围:
①首先要考虑自变量的取值必须使解析式有意义.
函数关系式是整式,自变量取值是 全体实数 .
函数关系式含有分式,自变量取值应使得 分母 不等于0.
函数关系式含有偶次根式,自变量取值应使得 被开方数 为非负数.
例如:有意义,则自变量x的取值范围是 x≥0 .
有意义,则自变量的取值范围是 x≠0 .
②实际问题的函数式,使实际问题有意义.
(3)常量与变量:常量:在某变化过程中 不变 的量.变量:在某变化过程中 变化 的量.
(4)描点法画函数图象的一般步骤是__列表_、__描点__、_连线_.
(5)函数的三种表示方法:① 列表法 ;② 图象法 ;③ 解析法 .
1、下列图象中,表示y是x的函数的个数有( B )
A.1个 B.2个 C.3个 D.4个
2、函数的图像在( A )
第一象限 B.第一、三象限 C.第二象限 D.第二、四象限
3、函数中,自变量x的取值范围是 x≤2且x≠-1 .
4、函数中,自变量x的取值范围是 x<1且x≠0
一次函数
1.一次函数和正比例函数的定义
一般地,如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.
特别地,当b=0时,一次函数y=kx+b就成为y=kx(k是常数,k≠0),这时y叫做x的正比例函数.
2.一次函数的图象与性质
(1)一次函数的图象
①一次函数y=kx+b(k≠0)的图象是经过点(0,b)和的一条直线.它的倾斜程度由k决定,b决定该直线与y轴交点的位置.
②正比例函数y=kx(k≠0)的图象是经过点(0,0)和(1,k)的一条直线.
一次函数的图象与性质
k、b的符号 k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0
图像的大致位置
经过象限 第一、二、三象限 第一、三、四象限 第一、二、四象限 第二、三、四象限
性质 y随x的增大而增大 y随x的增大而增大 y随x的增大而减小 y随x的增大而减小
3. 直线与坐标轴围成的三角形面积:
直线y=kx+b与x轴交点为(,0),与y轴交点为(0,b),且这两个交点与坐标原点构成的三角形面积为
S△= ·││·│b│.
4.一次函数解析式的确定:常用待定系数法求一次函数的解析式
1、下面函数图象不经过第二象限的为 ( )
(A) y=3x+2 (B) y=3x-2 (C) y=-3x+2 (D) y=-3x-2
2、一次函数y=kx+b的图象经过点(2,-1)和(0,3),那么这个一次函数的解析式为______
3、已知直线y=kx+b经过第一、二、四象限,那么直线y=-bx+k经过第_______象限。
4、一次函数y= -2x+4的图象与x轴交点坐标是 ,与y轴交点坐标是 图象与坐标轴所围成的三角形面积是 .
反比例函数
1.反比例函数的概念
一般地,如果两个变量x、y之间的关系可以表示成 或 (k为常数,k≠0)的形式,那么称y是x的反比例函数.
反比例函数解析式可以写成xy=k(k≠0),它表明在反比例函数中自变量x与其对应函数值y之积,总等于已知常数k.反比例函数解析式还可以写成(k≠0).
2.反比例函数的图象和性质
(1)图象:反比例函数的图象是双曲线.
(2)性质:
性质1:
k的符号 k>0 k<0
图像的大致位置
经过象限 第一、第三 象限 第二、第四 象限
性质 在每一象限内y随x的增大而 减小 在每一象限内y随x的增大而 增大
注意:双曲线的两支和坐标轴无限靠近,但永远不能相交.
性质2:双曲线是轴对称图形,直线y=x或y=-x是它的对称轴;双曲线也是中心对称图形,对称中心是坐标原点.
3.的几何含义:反比例函数(k≠0)中比例系数k的几何意义,即过双曲线(k≠0)上任意一点P作x轴、y轴垂线,设垂足分别为A、B,则所得矩形OAPB的面积S矩形OAPB=.△OAP的面积S△OAP=.
1、已知点A(-3,y1),B(-2,y2),C(3,y3)都在反比例函数y=的图象上,则( ).
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
2、反比例函数在第一象限的图象如图所示,
则k的值可能是( )
A.1 B.2 C.3 D.4
3、点A在双曲线上,则正△AOB的
面积为 ,点B坐标为 。
㈡紧扣考点 专题讲解
1、如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为__________,△AOC的面积为_________.
2、如图,直线的解析表达式为,且与轴交于点,直线经过点,直线,交于点.
(1)求点的坐标;
(2)求直线的解析表达式;
(3)求的面积;
(4)在直线上存在异于点的另一点,使得与的面积相等,请直接写出点的坐
3、如图,在平面直角坐标系中,直线y= 2x —6与x轴、y轴分别相交于点A、B,点C在x轴上,若△ABC是等腰三角形,试求点C的坐标。
4、一次函数y=x+2的图像与x轴、y轴分别交于点A、B,以AB为边在第二象限内做等边△ABC
(1)求C点的坐标。
(2)在第二象限内有一点M(m,1),使S△ABM =S△ABC ,求M点的坐标。
5、如图,反比例函数y=的图象与经过原点的直线相交于点A、B,已知A的坐标为(﹣2,1),则点B的坐标为 .
6、如图,双曲线y=与直线y=mx相交于A,B两点,B点的坐标为(﹣2,﹣3),则A点的坐标为 .
7、函数与的图象交于点A、B,过点A
作AC⊥y轴,则△ABC的面积是 。
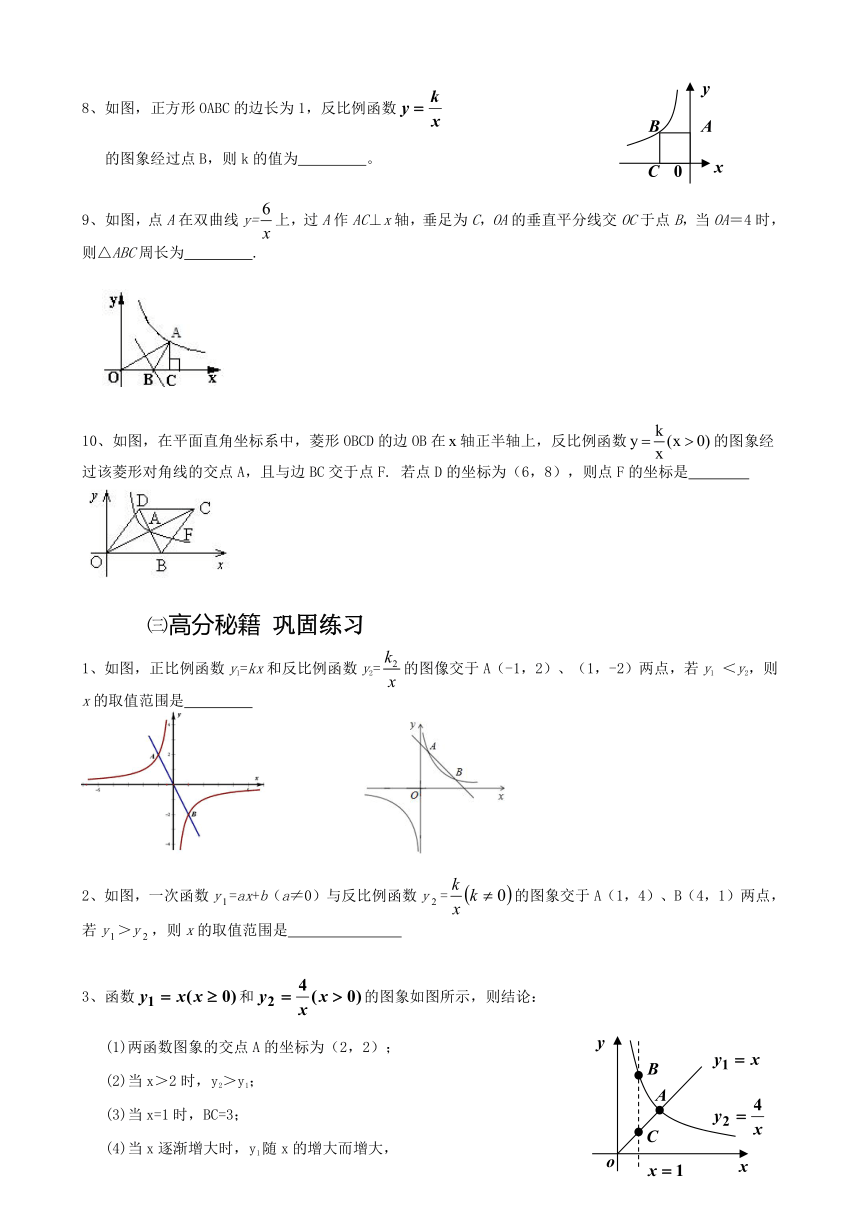
8、如图,正方形OABC的边长为1,反比例函数
的图象经过点B,则k的值为 。
如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,则△ABC周长为 .
10、如图,在平面直角坐标系中,菱形OBCD的边OB在轴正半轴上,反比例函数的图象经过该菱形对角线的交点A,且与边BC交于点F. 若点D的坐标为(6,8),则点F的坐标是
㈢高分秘籍 巩固练习
1、如图,正比例函数y1=kx和反比例函数y2=的图像交于A(-1,2)、(1,-2)两点,若y1 <y2,则x的取值范围是
2、如图,一次函数y=ax+b(a≠0)与反比例函数y=的图象交于A(1,4)、B(4,1)两点,若y>y,则x的取值范围是
3、函数和的图象如图所示,则结论:
(1)两函数图象的交点A的坐标为(2,2);
(2)当x>2时,y2>y1;
(3)当x=1时,BC=3;
(4)当x逐渐增大时,y1随x的增大而增大,
y2随x的增大而减小。
其中正确的结论的序号是 。
4、直线与双曲线交于点A(-4,n),B(2,-4)。
(1)求两个函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB面积;
(3)求方程的解;
(4) 求不等式的解集。
㈣精益求精 拓展提高
1、若函数y=-kx+2k+2与的图象有两个不同的交点,则k的取值范围是k> .
2、如果一次函数相交于点(),那么该直线与双曲线的另一个交点为__________.
3、 如图,在中,点是直线与双曲线在第一象限的交点,且,则A的坐标是_________.
4、直线y=ax(a>0)与双曲线y=交于A(x1,y1)、B(x2,y2)两点,则4x1y2-3x2y1=______.
5、如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数 ()的图象上,则点E的坐标是
如图,,,……在函数的图像上,,,,……都是等腰直角三角形,斜边、、,……都在轴上,求,P2 ,P3的坐标
【当堂过手训练】(快练10分钟,稳准建奇功!)
训练时间 学生姓名 过手分数 批改老师
1、若一次函数y=kx+b交于y轴的负半轴,且y的值随x的增大而减少,则k____0,b______0.(填“>”、“<”或“=”)
2、已知一次函数y=-x+a与y=x+b的图象相交于点(m,8),则a+b=_________.
3、直线y=-2x+4与两坐标轴围成的三角形的面积是________
4、如果直线y=-2x+k与两坐标轴所围成的三角形面积是9,则k的值为_____.
5、若m<-1,则函数① ②y=-mx+1, ③y=mx,④y=(m+1)x中,y随x增大而增大的是________.
6、在同一直角坐标系中,若函数y=k1x(k1≠0)的图象与(k2≠0)的图象没有公共点,则k1k2________0.
第一讲一次函数与反比例函数
㈠承上启下 知识回顾
函数基础知识
(1)函数:如果在一个变化过程中,有两个变量x、y,对于x的每一个确定的值 ,y都有 唯一确定的值 与之对应,此时称y是x的 函数,其中x是自变量,y是因变量.
(2)自变量的取值范围:
①首先要考虑自变量的取值必须使解析式有意义.
函数关系式是整式,自变量取值是 全体实数 .
函数关系式含有分式,自变量取值应使得 分母 不等于0.
函数关系式含有偶次根式,自变量取值应使得 被开方数 为非负数.
例如:有意义,则自变量x的取值范围是 x≥0 .
有意义,则自变量的取值范围是 x≠0 .
②实际问题的函数式,使实际问题有意义.
(3)常量与变量:常量:在某变化过程中 不变 的量.变量:在某变化过程中 变化 的量.
(4)描点法画函数图象的一般步骤是__列表_、__描点__、_连线_.
(5)函数的三种表示方法:① 列表法 ;② 图象法 ;③ 解析法 .
1、下列图象中,表示y是x的函数的个数有( B )
A.1个 B.2个 C.3个 D.4个
2、函数的图像在( A )
第一象限 B.第一、三象限 C.第二象限 D.第二、四象限
3、函数中,自变量x的取值范围是 x≤2且x≠-1 .
4、函数中,自变量x的取值范围是 x<1且x≠0
一次函数
1.一次函数和正比例函数的定义
一般地,如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.
特别地,当b=0时,一次函数y=kx+b就成为y=kx(k是常数,k≠0),这时y叫做x的正比例函数.
2.一次函数的图象与性质
(1)一次函数的图象
①一次函数y=kx+b(k≠0)的图象是经过点(0,b)和的一条直线.它的倾斜程度由k决定,b决定该直线与y轴交点的位置.
②正比例函数y=kx(k≠0)的图象是经过点(0,0)和(1,k)的一条直线.
一次函数的图象与性质
k、b的符号 k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0
图像的大致位置
经过象限 第一、二、三象限 第一、三、四象限 第一、二、四象限 第二、三、四象限
性质 y随x的增大而增大 y随x的增大而增大 y随x的增大而减小 y随x的增大而减小
3. 直线与坐标轴围成的三角形面积:
直线y=kx+b与x轴交点为(,0),与y轴交点为(0,b),且这两个交点与坐标原点构成的三角形面积为
S△= ·││·│b│.
4.一次函数解析式的确定:常用待定系数法求一次函数的解析式
1、下面函数图象不经过第二象限的为 ( D )
(A) y=3x+2 (B) y=3x-2 (C) y=-3x+2 (D) y=-3x-2
2、一次函数y=kx+b的图象经过点(2,-1)和(0,3),那么这个一次函数的解析式为_y=-2x+3______
3、已知直线y=kx+b经过第一、二、四象限,那么直线y=-bx+k经过第___二三四____象限。
4、一次函数y= -2x+4的图象与x轴交点坐标是 (2,0) ,与y轴交点坐标是 (0,4) 图象与坐标轴所围成的三角形面积是 4 .
反比例函数
1.反比例函数的概念
一般地,如果两个变量x、y之间的关系可以表示成或 xy=k (k为常数,k≠0)的形式,那么称y是x的反比例函数.
反比例函数解析式可以写成xy=k(k≠0),它表明在反比例函数中自变量x与其对应函数值y之积,总等于已知常数k.反比例函数解析式还可以写成(k≠0).
2.反比例函数的图象和性质
(1)图象:反比例函数的图象是双曲线.
(2)性质:
性质1:
k的符号 k>0 k<0
图像的大致位置
经过象限 第一、第三 象限 第二、第四 象限
性质 在每一象限内y随x的增大而 减小 在每一象限内y随x的增大而 增大
注意:双曲线的两支和坐标轴无限靠近,但永远不能相交.
性质2:双曲线是轴对称图形,直线y=x或y=-x是它的对称轴;双曲线也是中心对称图形,对称中心是坐标原点.
3.的几何含义:反比例函数(k≠0)中比例系数k的几何意义,即过双曲线(k≠0)上任意一点P作x轴、y轴垂线,设垂足分别为A、B,则所得矩形OAPB的面积S矩形OAPB=.△OAP的面积S△OAP=.
1、已知点A(-3,y1),B(-2,y2),C(3,y3)都在反比例函数y=的图象上,则( D ).
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
2、反比例函数在第一象限的图象如图所示,
则k的值可能是( C )
A.1 B.2 C.3 D.4
3、点A在双曲线上,则正△AOB的
面积为 √3 ,点B坐标为 (2,0) 。
㈡紧扣考点 专题讲解
1、如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为_____y=x+2_____,△AOC的面积为____4_____.
2、如图,直线的解析表达式为,且与轴交于点,直线经过点,直线,交于点.
(1)求点的坐标;
(2)求直线的解析表达式;
(3)求的面积;
(4)在直线上存在异于点的另一点,使得与的面积相等,请直接写出点的坐解:(1)由 ,令 ,得 .
. .
(2)设直线 的解析表达式为 ,由图象知: , ; , .
∴直线 的解析表达式为 .
(3)由 解得 . ,
.
(4) .
3、如图,在平面直角坐标系中,直线y= 2x —6与x轴、y轴分别相交于点A、B,点C在x轴上,若△ABC是等腰三角形,试求点C的坐标。
由题意,A(3,0),B(0.6)。AB=√(3?+6?)=3√5
△ABC为等腰三角形分三种情况:
①C在A的右边,AC=AB,则C的坐标为(3+3√5 ,0)
②C在A的右边,AC=AB,则C的坐标为(3-3√5,0)
③C在A的右边,AC=CB,设C为(x,0),原点为O。
根据勾股定理,得:OC?+OB?=BC?=AC?
x?+6?=(3+x)? => x=9/2 ,即C的坐标为(-9/2,0)。
4、一次函数y=x+2的图像与x轴、y轴分别交于点A、B,以AB为边在第二象限内做等边△ABC
(1)求C点的坐标。
(2)在第二象限内有一点M(m,1),使S△ABM =S△ABC ,求M点的坐标。
(1)、设C(-x,x)因为CA=AB
所以x?+(x-2)?=8
解得
x=√2-1因为设的x为正,c点为(-√2+1,√2-1)
(2)、CM‖AB
m=3-2√2
M(3-2√2,1)
5、如图,反比例函数y=的图象与经过原点的直线相交于点A、B,已知A的坐标为(﹣2,1),则点B的坐标为 (2,-1) .
6、如图,双曲线y=与直线y=mx相交于A,B两点,B点的坐标为(﹣2,﹣3),则A点的坐标为 (2,3) .
7、函数与的图象交于点A、B,过点A
作AC⊥y轴,则△ABC的面积是 2 。
8、如图,正方形OABC的边长为1,反比例函数
的图象经过点B,则k的值为 -1 。
如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,则△ABC周长为 2√7 .
10、如图,在平面直角坐标系中,菱形OBCD的边OB在轴正半轴上,反比例函数的图象经过该菱形对角线的交点A,且与边BC交于点F. 若点D的坐标为(6,8),则点F的坐标是 (12,8/3)
㈢高分秘籍 巩固练习
1、如图,正比例函数y1=kx和反比例函数y2=的图像交于A(-1,2)、(1,-2)两点,若y1 <y2,则x的取值范围是 x<-1或0<x<1
2、如图,一次函数y=ax+b(a≠0)与反比例函数y=的图象交于A(1,4)、B(4,1)两点,若y>y,则x的取值范围是 x<0或1<x<4
3、函数和的图象如图所示,则结论:
(1)两函数图象的交点A的坐标为(2,2);
(2)当x>2时,y2>y1;
(3)当x=1时,BC=3;
(4)当x逐渐增大时,y1随x的增大而增大,
y2随x的增大而减小。
其中正确的结论的序号是 1,3,4 。
4、直线与双曲线交于点A(-4,n),B(2,-4)。
(1)求两个函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB面积;
(3)求方程的解;
(4) 求不等式的解集。
1)由图象得:n+1<0,解得:n<-1。
由y=kx+k,令y=0,解得:,∴A坐标为(-1,0)。
(2)设C(a,b),
∵,∴ab=-8。
∵点C在双曲线上,∴双曲线的解析式为。
(3)∵CB⊥y轴,∴B(0,b)。
在Rt△AOB中,AB=,OA=1,根据勾股定理得:OB=4。
∴B(0,-4)。∴C(2,-4)。
将C代入直线y=kx+k中,得:2k+k=-4,即。
∴直线AC解析式为。
联立直线与反比例解析式得:,解得:或。
∴D(-3,)。
则由图象可得:当x<-3或0<x<2时,反比例函数的值小于一次函数的值。
㈣精益求精 拓展提高
1、若函数y=-kx+2k+2与的图象有两个不同的交点,则k的取值范围是k>- 0.5且k≠0 .
2、如果一次函数相交于点(),那么该直线与双曲线的另一个交点为___(-1,1)_______.
3、 如图,在中,点是直线与双曲线在第一象限的交点,且,则A的坐标是___4_______.
4、直线y=ax(a>0)与双曲线y=交于A(x1,y1)、B(x2,y2)两点,则4x1y2-3x2y1=__-3____.
5、如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数 ()的图象上,则点E的坐标是
6、如图,,,……在函数的图像上,,,,……都是等腰直角三角形,斜边、、,……都在轴上,求,P2 ,P3的坐标
【当堂过手训练】(快练10分钟,稳准建奇功!)
训练时间 学生姓名 过手分数 批改老师
1、若一次函数y=kx+b交于y轴的负半轴,且y的值随x的增大而减少,则k_<___0,b___<___0.(填“>”、“<”或“=”)
2、已知一次函数y=-x+a与y=x+b的图象相交于点(m,8),则a+b=_____16____.
3、直线y=-2x+4与两坐标轴围成的三角形的面积是__4_______
4、如果直线y=-2x+k与两坐标轴所围成的三角形面积是9,则k的值为_____.
5、若m<-1,则函数① ②y=-mx+1, ③y=mx,④y=(m+1)x中,y随x增大而增大的是_①____②___.
6、在同一直角坐标系中,若函数y=k1x(k1≠0)的图象与(k2≠0)的图象没有公共点,则k1k2___<_____0.
㈠承上启下 知识回顾
函数基础知识
(1)函数:如果在一个变化过程中,有两个变量x、y,对于x的每一个确定的值 ,y都有 唯一确定的值 与之对应,此时称y是x的 函数,其中x是自变量,y是因变量.
(2)自变量的取值范围:
①首先要考虑自变量的取值必须使解析式有意义.
函数关系式是整式,自变量取值是 全体实数 .
函数关系式含有分式,自变量取值应使得 分母 不等于0.
函数关系式含有偶次根式,自变量取值应使得 被开方数 为非负数.
例如:有意义,则自变量x的取值范围是 x≥0 .
有意义,则自变量的取值范围是 x≠0 .
②实际问题的函数式,使实际问题有意义.
(3)常量与变量:常量:在某变化过程中 不变 的量.变量:在某变化过程中 变化 的量.
(4)描点法画函数图象的一般步骤是__列表_、__描点__、_连线_.
(5)函数的三种表示方法:① 列表法 ;② 图象法 ;③ 解析法 .
1、下列图象中,表示y是x的函数的个数有( B )
A.1个 B.2个 C.3个 D.4个
2、函数的图像在( A )
第一象限 B.第一、三象限 C.第二象限 D.第二、四象限
3、函数中,自变量x的取值范围是 x≤2且x≠-1 .
4、函数中,自变量x的取值范围是 x<1且x≠0
一次函数
1.一次函数和正比例函数的定义
一般地,如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.
特别地,当b=0时,一次函数y=kx+b就成为y=kx(k是常数,k≠0),这时y叫做x的正比例函数.
2.一次函数的图象与性质
(1)一次函数的图象
①一次函数y=kx+b(k≠0)的图象是经过点(0,b)和的一条直线.它的倾斜程度由k决定,b决定该直线与y轴交点的位置.
②正比例函数y=kx(k≠0)的图象是经过点(0,0)和(1,k)的一条直线.
一次函数的图象与性质
k、b的符号 k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0
图像的大致位置
经过象限 第一、二、三象限 第一、三、四象限 第一、二、四象限 第二、三、四象限
性质 y随x的增大而增大 y随x的增大而增大 y随x的增大而减小 y随x的增大而减小
3. 直线与坐标轴围成的三角形面积:
直线y=kx+b与x轴交点为(,0),与y轴交点为(0,b),且这两个交点与坐标原点构成的三角形面积为
S△= ·││·│b│.
4.一次函数解析式的确定:常用待定系数法求一次函数的解析式
1、下面函数图象不经过第二象限的为 ( )
(A) y=3x+2 (B) y=3x-2 (C) y=-3x+2 (D) y=-3x-2
2、一次函数y=kx+b的图象经过点(2,-1)和(0,3),那么这个一次函数的解析式为______
3、已知直线y=kx+b经过第一、二、四象限,那么直线y=-bx+k经过第_______象限。
4、一次函数y= -2x+4的图象与x轴交点坐标是 ,与y轴交点坐标是 图象与坐标轴所围成的三角形面积是 .
反比例函数
1.反比例函数的概念
一般地,如果两个变量x、y之间的关系可以表示成 或 (k为常数,k≠0)的形式,那么称y是x的反比例函数.
反比例函数解析式可以写成xy=k(k≠0),它表明在反比例函数中自变量x与其对应函数值y之积,总等于已知常数k.反比例函数解析式还可以写成(k≠0).
2.反比例函数的图象和性质
(1)图象:反比例函数的图象是双曲线.
(2)性质:
性质1:
k的符号 k>0 k<0
图像的大致位置
经过象限 第一、第三 象限 第二、第四 象限
性质 在每一象限内y随x的增大而 减小 在每一象限内y随x的增大而 增大
注意:双曲线的两支和坐标轴无限靠近,但永远不能相交.
性质2:双曲线是轴对称图形,直线y=x或y=-x是它的对称轴;双曲线也是中心对称图形,对称中心是坐标原点.
3.的几何含义:反比例函数(k≠0)中比例系数k的几何意义,即过双曲线(k≠0)上任意一点P作x轴、y轴垂线,设垂足分别为A、B,则所得矩形OAPB的面积S矩形OAPB=.△OAP的面积S△OAP=.
1、已知点A(-3,y1),B(-2,y2),C(3,y3)都在反比例函数y=的图象上,则( ).
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
2、反比例函数在第一象限的图象如图所示,
则k的值可能是( )
A.1 B.2 C.3 D.4
3、点A在双曲线上,则正△AOB的
面积为 ,点B坐标为 。
㈡紧扣考点 专题讲解
1、如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为__________,△AOC的面积为_________.
2、如图,直线的解析表达式为,且与轴交于点,直线经过点,直线,交于点.
(1)求点的坐标;
(2)求直线的解析表达式;
(3)求的面积;
(4)在直线上存在异于点的另一点,使得与的面积相等,请直接写出点的坐
3、如图,在平面直角坐标系中,直线y= 2x —6与x轴、y轴分别相交于点A、B,点C在x轴上,若△ABC是等腰三角形,试求点C的坐标。
4、一次函数y=x+2的图像与x轴、y轴分别交于点A、B,以AB为边在第二象限内做等边△ABC
(1)求C点的坐标。
(2)在第二象限内有一点M(m,1),使S△ABM =S△ABC ,求M点的坐标。
5、如图,反比例函数y=的图象与经过原点的直线相交于点A、B,已知A的坐标为(﹣2,1),则点B的坐标为 .
6、如图,双曲线y=与直线y=mx相交于A,B两点,B点的坐标为(﹣2,﹣3),则A点的坐标为 .
7、函数与的图象交于点A、B,过点A
作AC⊥y轴,则△ABC的面积是 。
8、如图,正方形OABC的边长为1,反比例函数
的图象经过点B,则k的值为 。
如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,则△ABC周长为 .
10、如图,在平面直角坐标系中,菱形OBCD的边OB在轴正半轴上,反比例函数的图象经过该菱形对角线的交点A,且与边BC交于点F. 若点D的坐标为(6,8),则点F的坐标是
㈢高分秘籍 巩固练习
1、如图,正比例函数y1=kx和反比例函数y2=的图像交于A(-1,2)、(1,-2)两点,若y1 <y2,则x的取值范围是
2、如图,一次函数y=ax+b(a≠0)与反比例函数y=的图象交于A(1,4)、B(4,1)两点,若y>y,则x的取值范围是
3、函数和的图象如图所示,则结论:
(1)两函数图象的交点A的坐标为(2,2);
(2)当x>2时,y2>y1;
(3)当x=1时,BC=3;
(4)当x逐渐增大时,y1随x的增大而增大,
y2随x的增大而减小。
其中正确的结论的序号是 。
4、直线与双曲线交于点A(-4,n),B(2,-4)。
(1)求两个函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB面积;
(3)求方程的解;
(4) 求不等式的解集。
㈣精益求精 拓展提高
1、若函数y=-kx+2k+2与的图象有两个不同的交点,则k的取值范围是k> .
2、如果一次函数相交于点(),那么该直线与双曲线的另一个交点为__________.
3、 如图,在中,点是直线与双曲线在第一象限的交点,且,则A的坐标是_________.
4、直线y=ax(a>0)与双曲线y=交于A(x1,y1)、B(x2,y2)两点,则4x1y2-3x2y1=______.
5、如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数 ()的图象上,则点E的坐标是
如图,,,……在函数的图像上,,,,……都是等腰直角三角形,斜边、、,……都在轴上,求,P2 ,P3的坐标
【当堂过手训练】(快练10分钟,稳准建奇功!)
训练时间 学生姓名 过手分数 批改老师
1、若一次函数y=kx+b交于y轴的负半轴,且y的值随x的增大而减少,则k____0,b______0.(填“>”、“<”或“=”)
2、已知一次函数y=-x+a与y=x+b的图象相交于点(m,8),则a+b=_________.
3、直线y=-2x+4与两坐标轴围成的三角形的面积是________
4、如果直线y=-2x+k与两坐标轴所围成的三角形面积是9,则k的值为_____.
5、若m<-1,则函数① ②y=-mx+1, ③y=mx,④y=(m+1)x中,y随x增大而增大的是________.
6、在同一直角坐标系中,若函数y=k1x(k1≠0)的图象与(k2≠0)的图象没有公共点,则k1k2________0.
第一讲一次函数与反比例函数
㈠承上启下 知识回顾
函数基础知识
(1)函数:如果在一个变化过程中,有两个变量x、y,对于x的每一个确定的值 ,y都有 唯一确定的值 与之对应,此时称y是x的 函数,其中x是自变量,y是因变量.
(2)自变量的取值范围:
①首先要考虑自变量的取值必须使解析式有意义.
函数关系式是整式,自变量取值是 全体实数 .
函数关系式含有分式,自变量取值应使得 分母 不等于0.
函数关系式含有偶次根式,自变量取值应使得 被开方数 为非负数.
例如:有意义,则自变量x的取值范围是 x≥0 .
有意义,则自变量的取值范围是 x≠0 .
②实际问题的函数式,使实际问题有意义.
(3)常量与变量:常量:在某变化过程中 不变 的量.变量:在某变化过程中 变化 的量.
(4)描点法画函数图象的一般步骤是__列表_、__描点__、_连线_.
(5)函数的三种表示方法:① 列表法 ;② 图象法 ;③ 解析法 .
1、下列图象中,表示y是x的函数的个数有( B )
A.1个 B.2个 C.3个 D.4个
2、函数的图像在( A )
第一象限 B.第一、三象限 C.第二象限 D.第二、四象限
3、函数中,自变量x的取值范围是 x≤2且x≠-1 .
4、函数中,自变量x的取值范围是 x<1且x≠0
一次函数
1.一次函数和正比例函数的定义
一般地,如果y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数.
特别地,当b=0时,一次函数y=kx+b就成为y=kx(k是常数,k≠0),这时y叫做x的正比例函数.
2.一次函数的图象与性质
(1)一次函数的图象
①一次函数y=kx+b(k≠0)的图象是经过点(0,b)和的一条直线.它的倾斜程度由k决定,b决定该直线与y轴交点的位置.
②正比例函数y=kx(k≠0)的图象是经过点(0,0)和(1,k)的一条直线.
一次函数的图象与性质
k、b的符号 k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0
图像的大致位置
经过象限 第一、二、三象限 第一、三、四象限 第一、二、四象限 第二、三、四象限
性质 y随x的增大而增大 y随x的增大而增大 y随x的增大而减小 y随x的增大而减小
3. 直线与坐标轴围成的三角形面积:
直线y=kx+b与x轴交点为(,0),与y轴交点为(0,b),且这两个交点与坐标原点构成的三角形面积为
S△= ·││·│b│.
4.一次函数解析式的确定:常用待定系数法求一次函数的解析式
1、下面函数图象不经过第二象限的为 ( D )
(A) y=3x+2 (B) y=3x-2 (C) y=-3x+2 (D) y=-3x-2
2、一次函数y=kx+b的图象经过点(2,-1)和(0,3),那么这个一次函数的解析式为_y=-2x+3______
3、已知直线y=kx+b经过第一、二、四象限,那么直线y=-bx+k经过第___二三四____象限。
4、一次函数y= -2x+4的图象与x轴交点坐标是 (2,0) ,与y轴交点坐标是 (0,4) 图象与坐标轴所围成的三角形面积是 4 .
反比例函数
1.反比例函数的概念
一般地,如果两个变量x、y之间的关系可以表示成或 xy=k (k为常数,k≠0)的形式,那么称y是x的反比例函数.
反比例函数解析式可以写成xy=k(k≠0),它表明在反比例函数中自变量x与其对应函数值y之积,总等于已知常数k.反比例函数解析式还可以写成(k≠0).
2.反比例函数的图象和性质
(1)图象:反比例函数的图象是双曲线.
(2)性质:
性质1:
k的符号 k>0 k<0
图像的大致位置
经过象限 第一、第三 象限 第二、第四 象限
性质 在每一象限内y随x的增大而 减小 在每一象限内y随x的增大而 增大
注意:双曲线的两支和坐标轴无限靠近,但永远不能相交.
性质2:双曲线是轴对称图形,直线y=x或y=-x是它的对称轴;双曲线也是中心对称图形,对称中心是坐标原点.
3.的几何含义:反比例函数(k≠0)中比例系数k的几何意义,即过双曲线(k≠0)上任意一点P作x轴、y轴垂线,设垂足分别为A、B,则所得矩形OAPB的面积S矩形OAPB=.△OAP的面积S△OAP=.
1、已知点A(-3,y1),B(-2,y2),C(3,y3)都在反比例函数y=的图象上,则( D ).
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
2、反比例函数在第一象限的图象如图所示,
则k的值可能是( C )
A.1 B.2 C.3 D.4
3、点A在双曲线上,则正△AOB的
面积为 √3 ,点B坐标为 (2,0) 。
㈡紧扣考点 专题讲解
1、如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为_____y=x+2_____,△AOC的面积为____4_____.
2、如图,直线的解析表达式为,且与轴交于点,直线经过点,直线,交于点.
(1)求点的坐标;
(2)求直线的解析表达式;
(3)求的面积;
(4)在直线上存在异于点的另一点,使得与的面积相等,请直接写出点的坐解:(1)由 ,令 ,得 .
. .
(2)设直线 的解析表达式为 ,由图象知: , ; , .
∴直线 的解析表达式为 .
(3)由 解得 . ,
.
(4) .
3、如图,在平面直角坐标系中,直线y= 2x —6与x轴、y轴分别相交于点A、B,点C在x轴上,若△ABC是等腰三角形,试求点C的坐标。
由题意,A(3,0),B(0.6)。AB=√(3?+6?)=3√5
△ABC为等腰三角形分三种情况:
①C在A的右边,AC=AB,则C的坐标为(3+3√5 ,0)
②C在A的右边,AC=AB,则C的坐标为(3-3√5,0)
③C在A的右边,AC=CB,设C为(x,0),原点为O。
根据勾股定理,得:OC?+OB?=BC?=AC?
x?+6?=(3+x)? => x=9/2 ,即C的坐标为(-9/2,0)。
4、一次函数y=x+2的图像与x轴、y轴分别交于点A、B,以AB为边在第二象限内做等边△ABC
(1)求C点的坐标。
(2)在第二象限内有一点M(m,1),使S△ABM =S△ABC ,求M点的坐标。
(1)、设C(-x,x)因为CA=AB
所以x?+(x-2)?=8
解得
x=√2-1因为设的x为正,c点为(-√2+1,√2-1)
(2)、CM‖AB
m=3-2√2
M(3-2√2,1)
5、如图,反比例函数y=的图象与经过原点的直线相交于点A、B,已知A的坐标为(﹣2,1),则点B的坐标为 (2,-1) .
6、如图,双曲线y=与直线y=mx相交于A,B两点,B点的坐标为(﹣2,﹣3),则A点的坐标为 (2,3) .
7、函数与的图象交于点A、B,过点A
作AC⊥y轴,则△ABC的面积是 2 。
8、如图,正方形OABC的边长为1,反比例函数
的图象经过点B,则k的值为 -1 。
如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,则△ABC周长为 2√7 .
10、如图,在平面直角坐标系中,菱形OBCD的边OB在轴正半轴上,反比例函数的图象经过该菱形对角线的交点A,且与边BC交于点F. 若点D的坐标为(6,8),则点F的坐标是 (12,8/3)
㈢高分秘籍 巩固练习
1、如图,正比例函数y1=kx和反比例函数y2=的图像交于A(-1,2)、(1,-2)两点,若y1 <y2,则x的取值范围是 x<-1或0<x<1
2、如图,一次函数y=ax+b(a≠0)与反比例函数y=的图象交于A(1,4)、B(4,1)两点,若y>y,则x的取值范围是 x<0或1<x<4
3、函数和的图象如图所示,则结论:
(1)两函数图象的交点A的坐标为(2,2);
(2)当x>2时,y2>y1;
(3)当x=1时,BC=3;
(4)当x逐渐增大时,y1随x的增大而增大,
y2随x的增大而减小。
其中正确的结论的序号是 1,3,4 。
4、直线与双曲线交于点A(-4,n),B(2,-4)。
(1)求两个函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB面积;
(3)求方程的解;
(4) 求不等式的解集。
1)由图象得:n+1<0,解得:n<-1。
由y=kx+k,令y=0,解得:,∴A坐标为(-1,0)。
(2)设C(a,b),
∵,∴ab=-8。
∵点C在双曲线上,∴双曲线的解析式为。
(3)∵CB⊥y轴,∴B(0,b)。
在Rt△AOB中,AB=,OA=1,根据勾股定理得:OB=4。
∴B(0,-4)。∴C(2,-4)。
将C代入直线y=kx+k中,得:2k+k=-4,即。
∴直线AC解析式为。
联立直线与反比例解析式得:,解得:或。
∴D(-3,)。
则由图象可得:当x<-3或0<x<2时,反比例函数的值小于一次函数的值。
㈣精益求精 拓展提高
1、若函数y=-kx+2k+2与的图象有两个不同的交点,则k的取值范围是k>- 0.5且k≠0 .
2、如果一次函数相交于点(),那么该直线与双曲线的另一个交点为___(-1,1)_______.
3、 如图,在中,点是直线与双曲线在第一象限的交点,且,则A的坐标是___4_______.
4、直线y=ax(a>0)与双曲线y=交于A(x1,y1)、B(x2,y2)两点,则4x1y2-3x2y1=__-3____.
5、如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数 ()的图象上,则点E的坐标是
6、如图,,,……在函数的图像上,,,,……都是等腰直角三角形,斜边、、,……都在轴上,求,P2 ,P3的坐标
【当堂过手训练】(快练10分钟,稳准建奇功!)
训练时间 学生姓名 过手分数 批改老师
1、若一次函数y=kx+b交于y轴的负半轴,且y的值随x的增大而减少,则k_<___0,b___<___0.(填“>”、“<”或“=”)
2、已知一次函数y=-x+a与y=x+b的图象相交于点(m,8),则a+b=_____16____.
3、直线y=-2x+4与两坐标轴围成的三角形的面积是__4_______
4、如果直线y=-2x+k与两坐标轴所围成的三角形面积是9,则k的值为_____.
5、若m<-1,则函数① ②y=-mx+1, ③y=mx,④y=(m+1)x中,y随x增大而增大的是_①____②___.
6、在同一直角坐标系中,若函数y=k1x(k1≠0)的图象与(k2≠0)的图象没有公共点,则k1k2___<_____0.
同课章节目录
