《二元一次方程与一次函数》（1）学案

初二数学第七章《二元一次方程与一次函数》（1）学案
班级 姓名 学号
学习目标:
1、初步理解二元一次方程与一次函数的关系。
2、能根据一次函数的图象求二元一次方程组的近似解。
学习重、难点:
1、二元一次方程和一次函数的关系。
2、能根据一次函数的图象求二元一次方程组的近似解。
3、方程和函数之间的对应关系即数形结合的意识和能力的培养。
学习过程:
一、阶段回顾：
1、已知一次函数y = 3－2x
(1)画出函数的图象．
(2)求图象与x轴、y轴的交点A、B的坐标．
(3)求△AOB的面积．
(4)利用图象求当x为何值时，。
二、探究活动
独立思考·解决问题
1、方程x+y=5的解有多少个？ ，请写出其中的三组整数解： 。
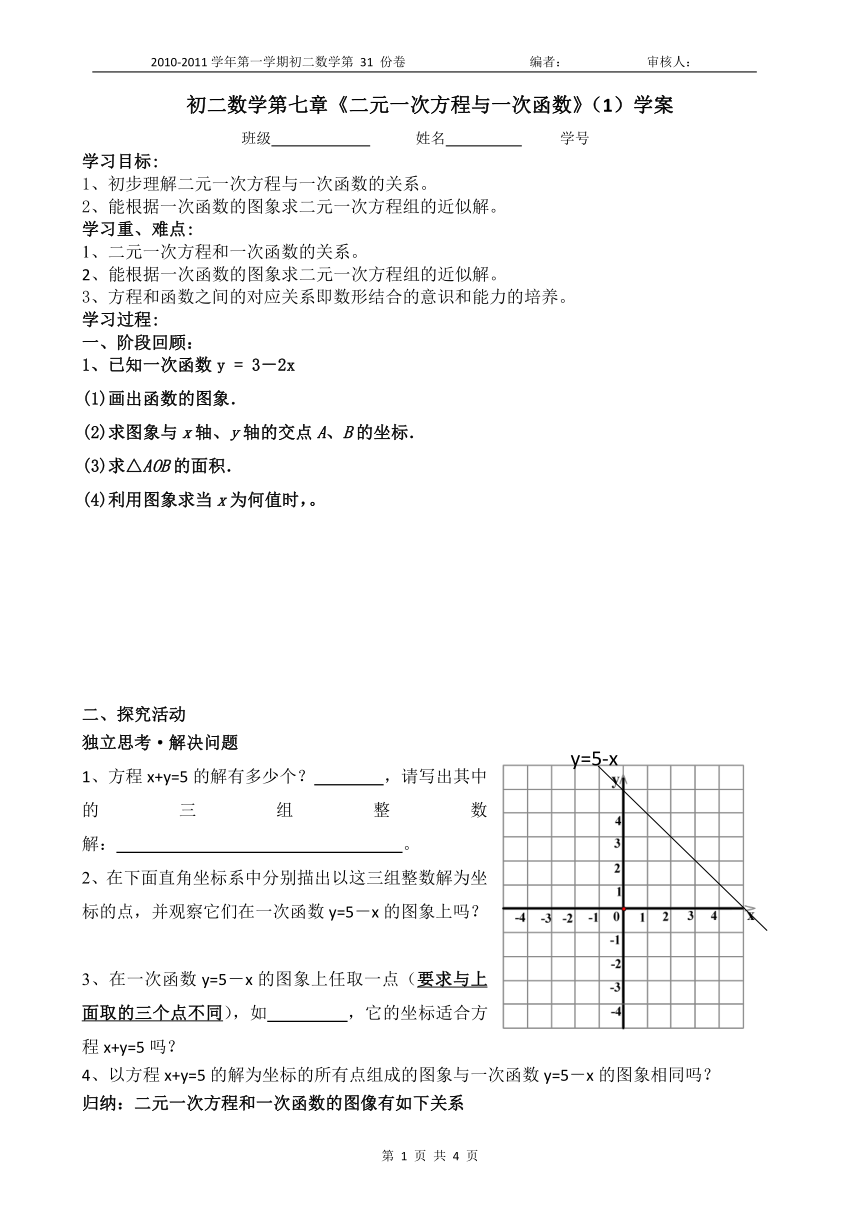
2、在下面直角坐标系中分别描出以这三组整数解为坐标的点，并观察它们在一次函数y=5－x的图象上吗？
3、在一次函数y=5－x的图象上任取一点（要求与上面取的三个点不同），如 ，它的坐标适合方程x+y=5吗？
4、以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5－x的图象相同吗？
归纳：二元一次方程和一次函数的图像有如下关系
以二元一次方程的解为坐标的点都在 ；
一次函数图像上的点的坐标都 。
师生探究·合作交流
做一做：
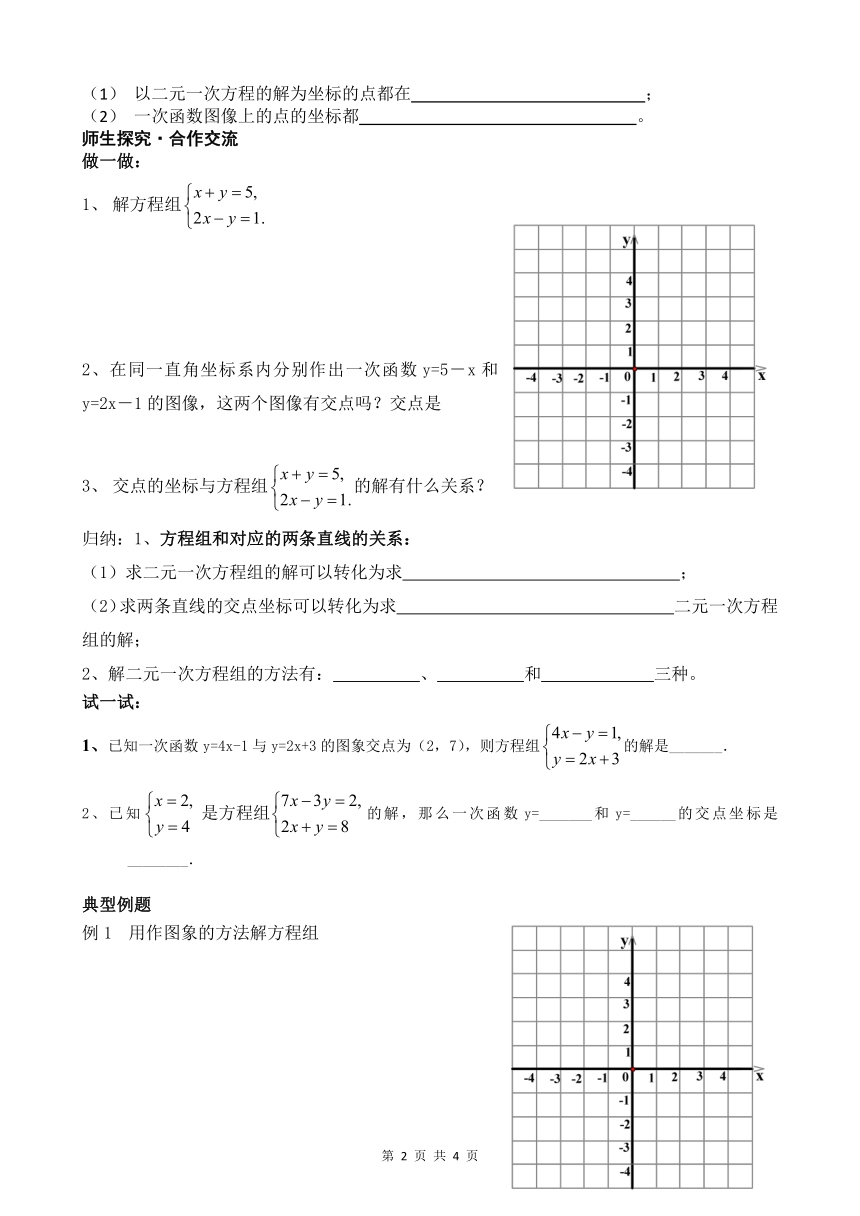
解方程组
2、在同一直角坐标系内分别作出一次函数y=5－x和y=2x－1的图像，这两个图像有交点吗？交点是
交点的坐标与方程组的解有什么关系？
归纳：1、方程组和对应的两条直线的关系：
（1）求二元一次方程组的解可以转化为求 ；
（2）求两条直线的交点坐标可以转化为求 二元一次方程组的解；
2、解二元一次方程组的方法有： 、 和 三种。
试一试：
1、已知一次函数y=4x-1与y=2x+3的图象交点为（2，7），则方程组的解是_______．
2、已知的解，那么一次函数y=_______和y=______的交点坐标是________．
典型例题
用作图象的方法解方程组
一般地，用作图法来解方程组的步骤如下：
把二元一次方程化成一次函数的形式
在直角坐标系中画出两个一次函数的图像，并标出交点。
交点坐标就是方程组的解。
试一试：
1、用作图象的方法解方程组
2、如图，直线与的交点坐标是 ．
三、学习体会：
1、本节课你有哪些收获？你还有哪些疑惑？
四、自我测试：
1、如右图所示，直线L1，L2的交点坐标可以看做方程组（ ）的解。
已知一次函数与的图像的交点为,则．
3、已知一次函数y=3x-5与y=2x+b的图象的交点为P（1，-2），则方程组的解是
是 ，b= 。
4、如果一次函数y=3x+6与y=2x-4的图象交点坐标为（a，b），则是方程组（ ）的解．
5、用作图象的方法解程组
五、应用拓展
1、已知一次函数y=2x-3和y=2x+1。
（1）在同一坐标系中画出两个函数的图象；
（2）根据图象回答，方程组的解存在吗？
2、求两条直线与和轴所围成的三角形面积。
2010-2011学年第一学期初二数学第 31 份卷 编者： 审核人：
y=5-x
第 1 页 共 4 页