平行线的性质

(共26张PPT)
请欣赏
　　图１
　图２
　　图３
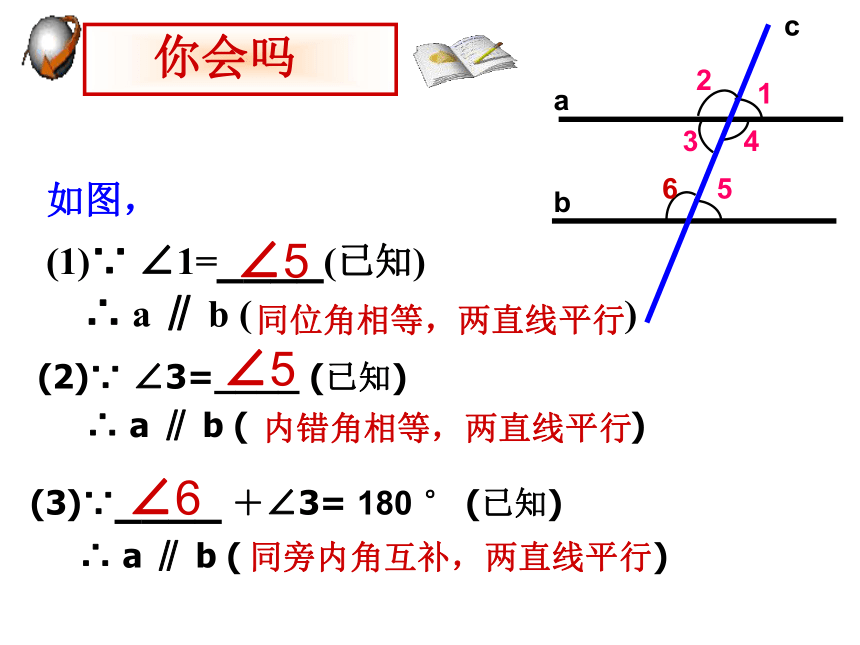
如图，
(1)∵ ∠1=____(已知)
∴ a ∥ b ( )
(2)∵ ∠3=____ (已知)
∴ a ∥ b ( )
(3)∵____ ＋∠3= 180 ° (已知)
∴ a ∥ b ( )
同位角相等，两直线平行
内错角相等，两直线平行
同旁内角互补，两直线平行
c
a
b
1
5
3
4
你会吗
2
6
∠5
∠5
∠6
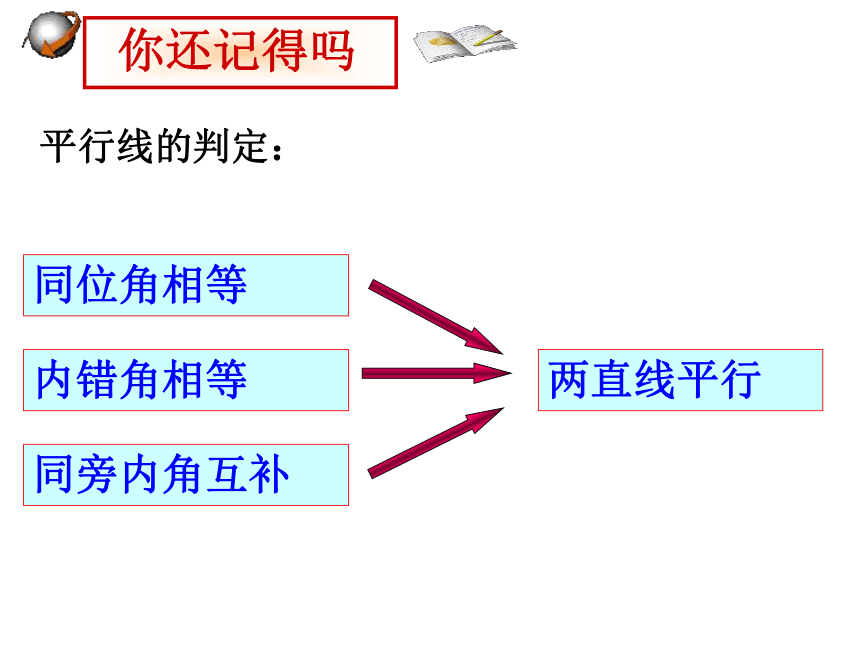
你还记得吗
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定：
a
c
b
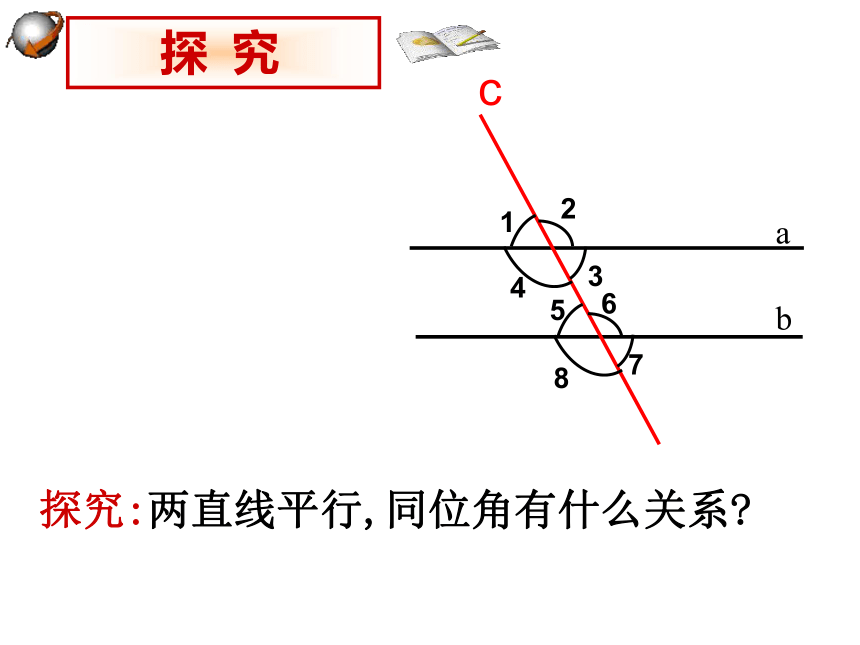
探究:两直线平行,同位角有什么关系
a
b
探 究
c
1
5
2
3
4
7
6
8
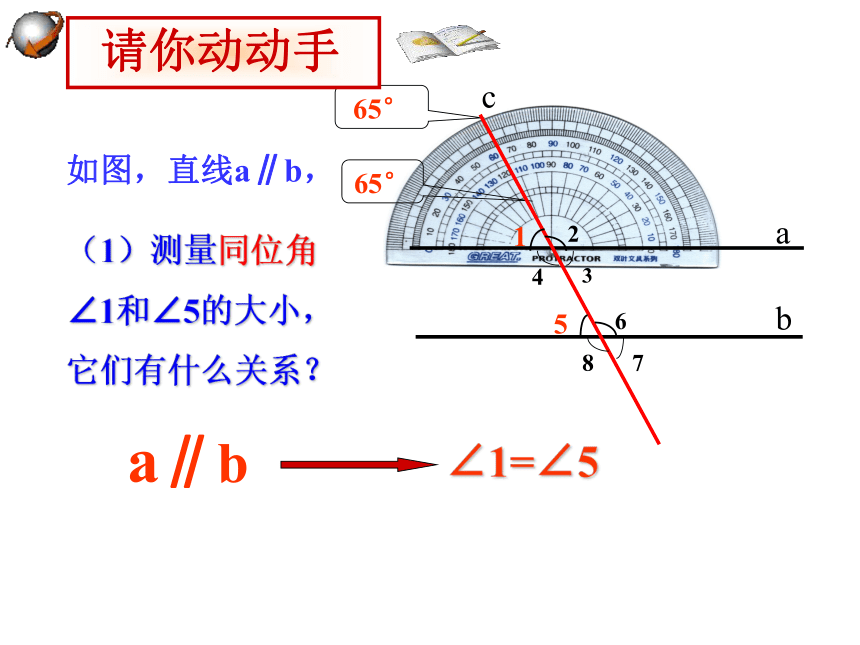
如图，直线a∥b，
（1）测量同位角∠1和∠5的大小，它们有什么关系？
65°
65°
c
a
b
1
5
2
4
3
6
8
7
∠1=∠5
a∥b
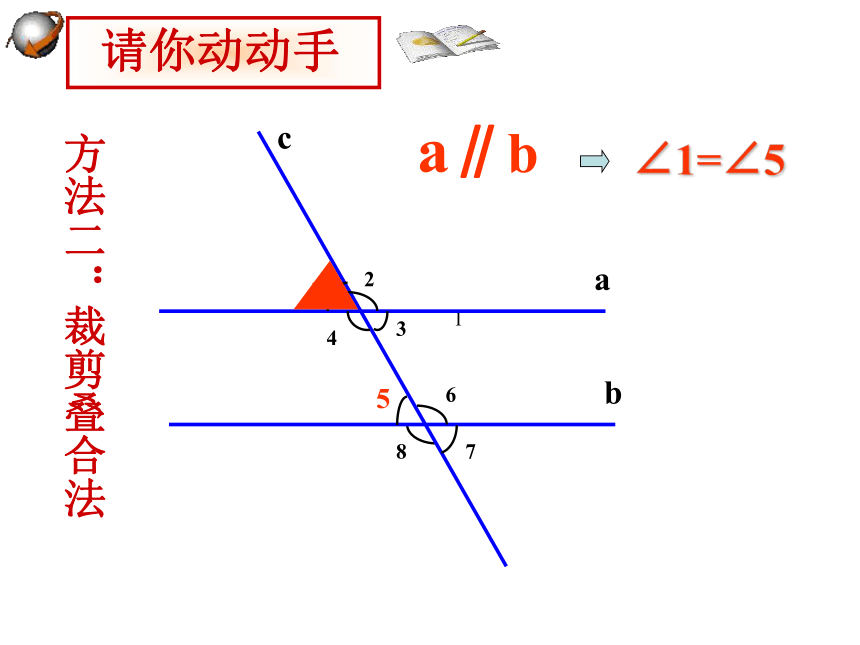
请你动动手
1
b
5
6
7
a
c
2
4
3
8
1
∠1=∠5
a∥b
请你动动手
方法二：裁剪叠合法
　简单地说：两直线平行，同位角相等．
a
b
1
2
3
4
得出结论
几何语言表述:
∵a∥b(已知)
∴∠１＝∠2（两直线平行，同位角相等）
两条平行线被第三条直线所截，同位角相等．
平行线性质1:
　两直线平行，同位角相等．
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
a
b
1
2
3
4
猜想并讨论
猜想:两直线平行，内错角、同旁内角有怎么关系呢？相互讨论一下.
性质１：两直线平行，同位角相等．
性质２：两直线平行，内错角相等．
性质３：两直线平行，同旁内角互补．
平行线的性质：
a
b
1
2
3
4
得出结论
利用性质1来说明性质2和性质3
a
b
1
2
3
4
已知: a ∥ b ,
请说明∠2=∠3.
∵ a ∥ b (已知)
∴∠1=∠2( )
∵ ∠1=∠3( )
∴∠2=∠3
两直线平行，同位角相等
对顶角相等
（等量代换）
推 导
如图，
(1)∵ a ∥ b (已知)
∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知)
∴ ∠2____∠3 ( )
(3)∵ a ∥ b (已知)
∴ ∠2＋∠4=____ ( )
=
两直线平行，同位角相等
=
两直线平行，内错角相等
180 °
两直线平行，同旁内角互补
c
a
b
1
2
3
4
书写方法
平行线的判定
（1）同位角相等，两直线平行；
（2）内错角相等，两直线平行；
（3）同旁内角互补，两直线平行。
条件
结论
两直线平行，同旁内角互补。
平行线的性质
两直线平行，同位角相等；
两直线平行，内错角相等；
结论
条件
两者比较
平行线的判定与平行线 的性质的比较：
平行线的判定与平行线的性质是因果互换的两类不同的定理，
判定是说：满足了什么条件（性质）的两条直线是互相平行的
性质是说：如果两条直线平行，就应该具有什么性质。
两者比较
1、如图，已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度 为什么？
(2)从∠1=110o可以知道 ∠3是多少度？为什么？
(3)从 ∠1=110 o可以知道∠4 是多少度？为什么？
一、快速抢答
2
E
1
3
4
A
B
D
C
∠2=110o
∵两直线行，内错角相等
∠3=110o
∵两直线平行,同位角相等
∠4=70o
∵两直线平行,同旁内角互补
一、快速抢答
2、如图，一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜，第二次 拐的角∠C是多少度？为什么？
Ｂ
Ｃ
∠C=142o
∵两直线平行,内错角相等
一、快速抢答
3、如图直线 a ∥ b,直线b垂直于直线c，则直线a垂直于直线c吗
∟
∟
a
b
c

a⊥b
∵两直线平行, 同位角相等
5、如图 ∵AB ∥CD，∴∠1=∠2 （两直线平行,内错角相等 ） （ ）
二、是是非非
Ａ
B
Ｃ
Ｄ
１
２
6、如图直线 a∥b,则∠1=∠2 .（ ）
×
×
1
2
a
b
1、如果有两条直线被第三条直线所截，那么必定有 （ ）
（A）内错角相等， (B)同位角相等，（C）同旁内角互补 （D）以上都不对.
三、选选看
D
三、选选看
2 、∠1 和∠2是两条直线被第三条直线
所截形成的同旁内角,要使这两条直线平
行,必须 ( )
A. ∠1= ∠2 B. ∠1+∠2=90o
C. 2(∠1+∠2)=360o D .∠1是钝角, ∠2是锐角
C
四、填填看
如图１,若AB∥DE ,　AC∥DF，请说出∠A和∠Ｄ之间的数量关系，并说明理由。
P
F
C
E
B
A
D
图１
解: ∠A =∠D. 理由：
∵ AB∥DE( 　)
∴∠A=____ ( )
∵AC∥DF( )
∴∠D=____ ( )
∴∠A=∠D ( )
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
四、填填看
如图2,若AB∥DE ,　AC∥DF，请说出∠A和∠Ｄ之间的数量关系，并说明理由。
图２
F
C
E
B
A
D
P
解: ∠A+∠D=180o. 理由：
∵ AB∥DE( 　)
∴∠A=____ ( )
∵AC∥DF( )
∴∠D+ ____=180o ( )
∴∠A+∠D=180o（ ）
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
如图。这是一付“角棋”。“棋盘”是一些平行线，“棋子”是用彩纸做成的两个角（ ∠1和∠2）。规则如下:从两头开始“跳”角, ∠ 1往下往右跳, ∠ 2往上往右跳,以跳到对方初始位置为胜，双方轮流进行，每“跳”
一步要说出“跳” 的根据（即平行线的性质等），看看谁“跳”得快，理由说得准确。
五、数学游戏
1
2
图形
已知
结果
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
）
）
）
）
）
）
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
六、小结
平行线的性质
六、小结
发现数学结论的方法:
1.数学实验(测量、叠合等)法
2.猜想、推理法
1、如图：
∵∠1＝∠2（　　　　）
∴AD∥　　　（　　　　　　　　　　　　）
∴∠BCD＋　　　＝180°（　　　　　　　　　　　　　　　）
A
B
C
D
1
2
已知
BC
∠D
内错角相等，两直线平行
两直线平行，同旁内角互补
四、填填看