人教版2020--2021八年级(下)数学第十八章《平行四边形》质量检测试卷A(含解析)
文档属性
| 名称 | 人教版2020--2021八年级(下)数学第十八章《平行四边形》质量检测试卷A(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 08:57:37 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版2020-20201年八年级(下)第十八章平行四边形检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1.
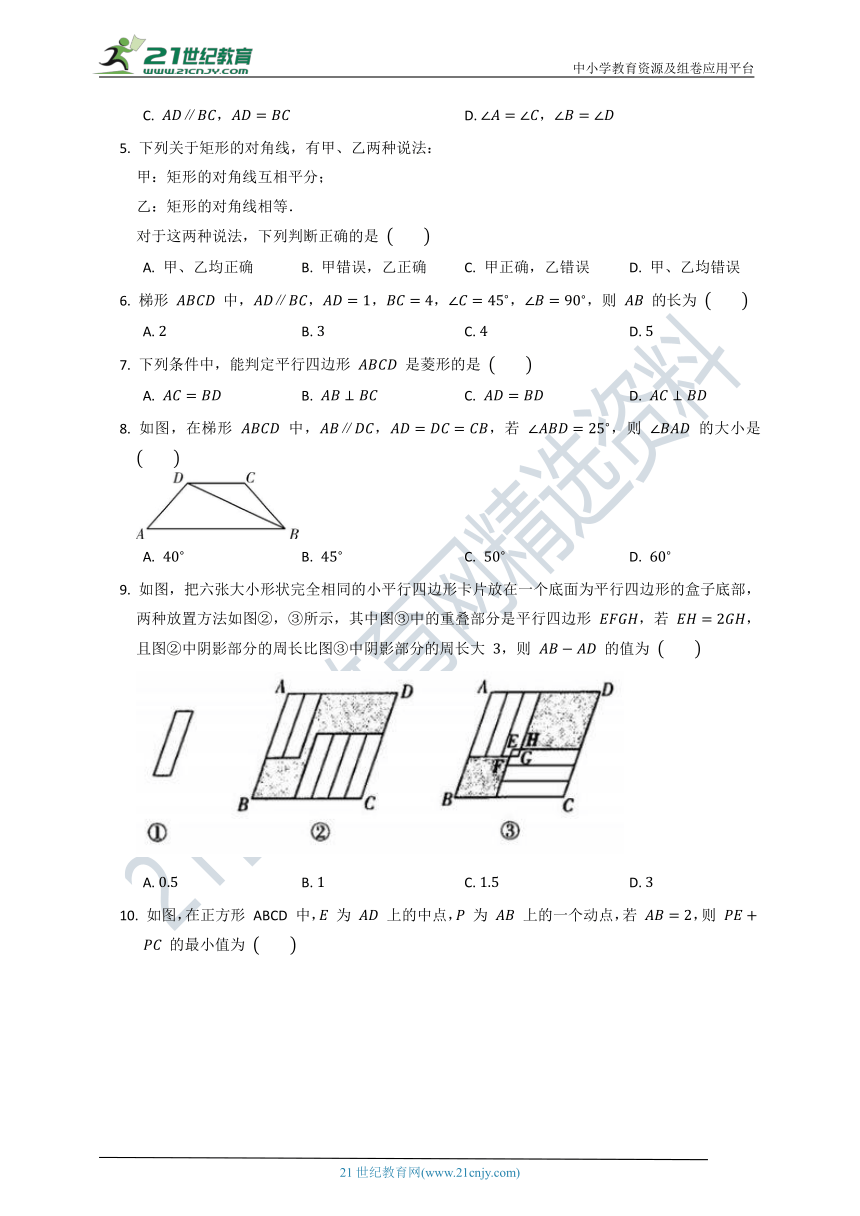
观察下列各方格图中阴影部分所示的图形(每一小方格的边长为
),如果将它们沿方格边线或对角线剪开重新拼接,不能拼成正方形的是
A.
B.
C.
D.
2.
如图,在直角
的内部有一滑动杆
,当端点
沿直线
向下滑动时,端点
会随之自动地沿直线
向左滑动,如果滑动杆从图中
处滑动到
处,那么滑动杆的中点
所经过的路径是
A.
直线的一部分
B.
圆的一部分
C.
双曲线的一部分
D.
抛物线的一部分
3.
如图,菱形
中,,则
A.
B.
C.
D.
4.
下列不能判定四边形
为平行四边形的条件是
A.
,
B.
,
C.
,
D.
,
5.
下列关于矩形的对角线,有甲、乙两种说法:
甲:矩形的对角线互相平分;
乙:矩形的对角线相等.
对于这两种说法,下列判断正确的是
A.
甲、乙均正确
B.
甲错误,乙正确
C.
甲正确,乙错误
D.
甲、乙均错误
6.
梯形
中,,,,,,则
的长为
A.
B.
C.
D.
7.
下列条件中,能判定平行四边形
是菱形的是
A.
B.
C.
D.
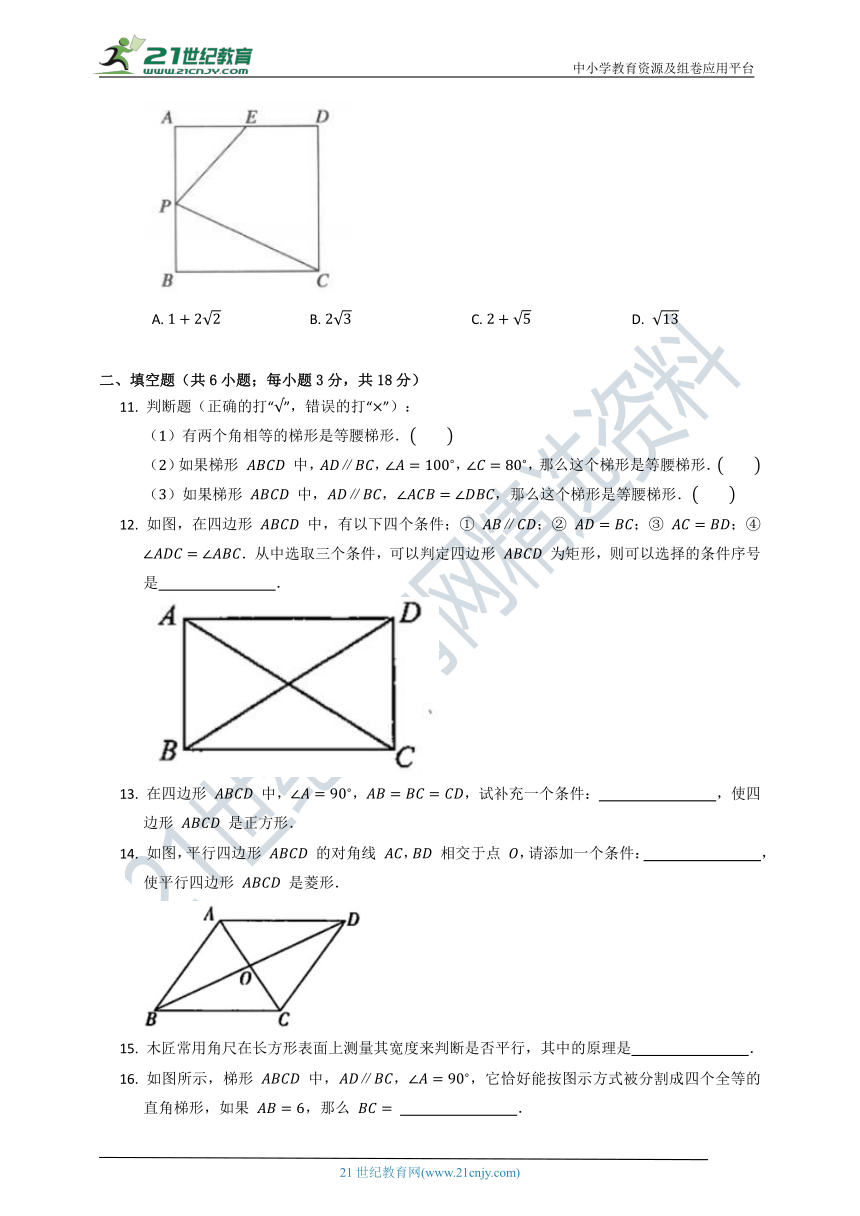
8.
如图,在梯形
中,,,若
,则
的大小是
A.
B.
C.
D.
9.
如图,把六张大小形状完全相同的小平行四边形卡片放在一个底面为平行四边形的盒子底部,两种放置方法如图②,③所示,其中图③中的重叠部分是平行四边形
,若
,且图②中阴影部分的周长比图③中阴影部分的周长大
,则
的值为
A.
B.
C.
D.
10.
如图,在正方形
ABCD
中,
为
上的中点,
为
上的一个动点,若
,则
的最小值为
A.
B.
C.
D.
二、填空题(共6小题;每小题3分,共18分)
11.
判断题(正确的打“”,错误的打“”):
()有两个角相等的梯形是等腰梯形.
()如果梯形
中,,,,那么这个梯形是等腰梯形.
()如果梯形
中,,,那么这个梯形是等腰梯形.
12.
如图,在四边形
中,有以下四个条件;①
;②
;③
;④
.从中选取三个条件,可以判定四边形
为矩形,则可以选择的条件序号是
?.
13.
在四边形
中,,,试补充一个条件:
?,使四边形
是正方形.
14.
如图,平行四边形
的对角线
,
相交于点
,请添加一个条件:
?,使平行四边形
是菱形.
15.
木匠常用角尺在长方形表面上测量其宽度来判断是否平行,其中的原理是
?.
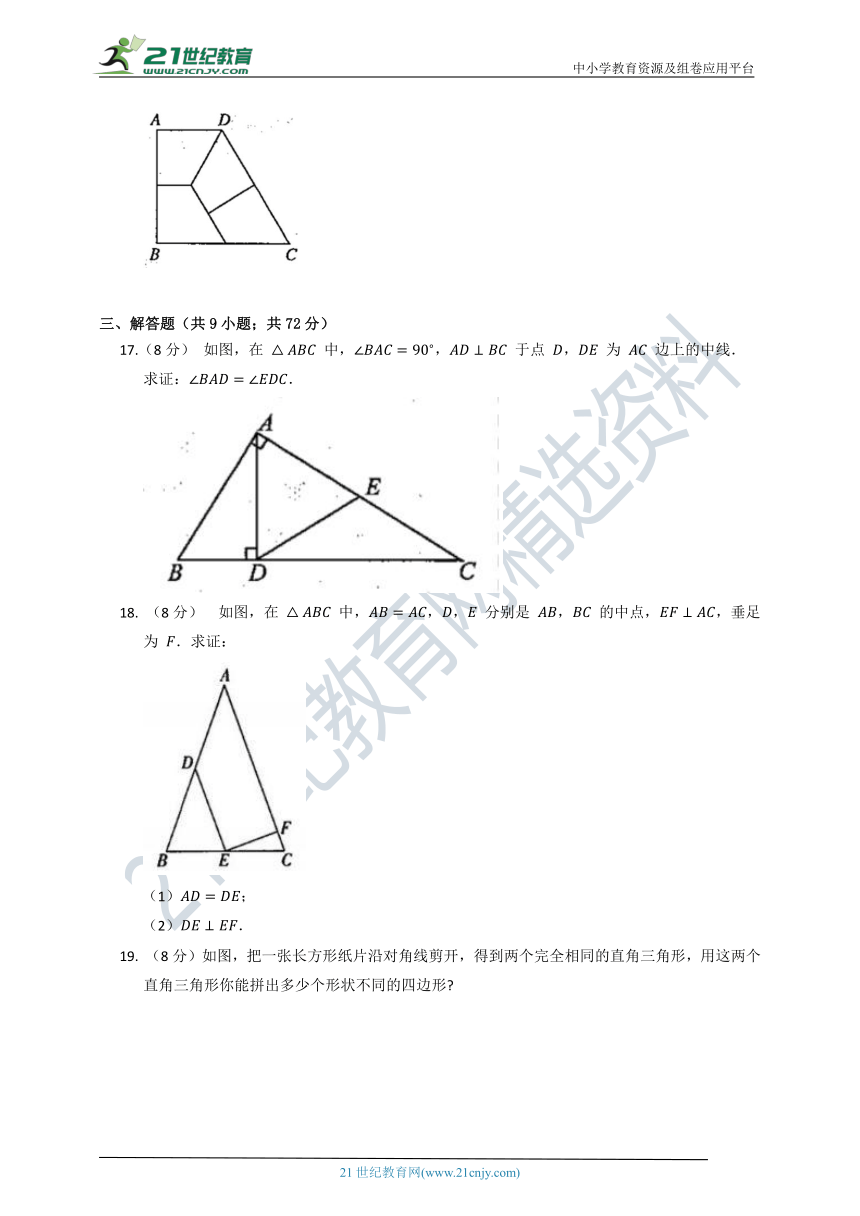
16.
如图所示,梯形
中,,,它恰好能按图示方式被分割成四个全等的直角梯形,如果
,那么
?.
三、解答题(共9小题;共72分)
17.(8分)
如图,在
中,,
于点
,
为
边上的中线.
求证:.
18.
(8分)
如图,在
中,,,
分别是
,
的中点,,垂足为
.求证:
(1);
(2).
19.
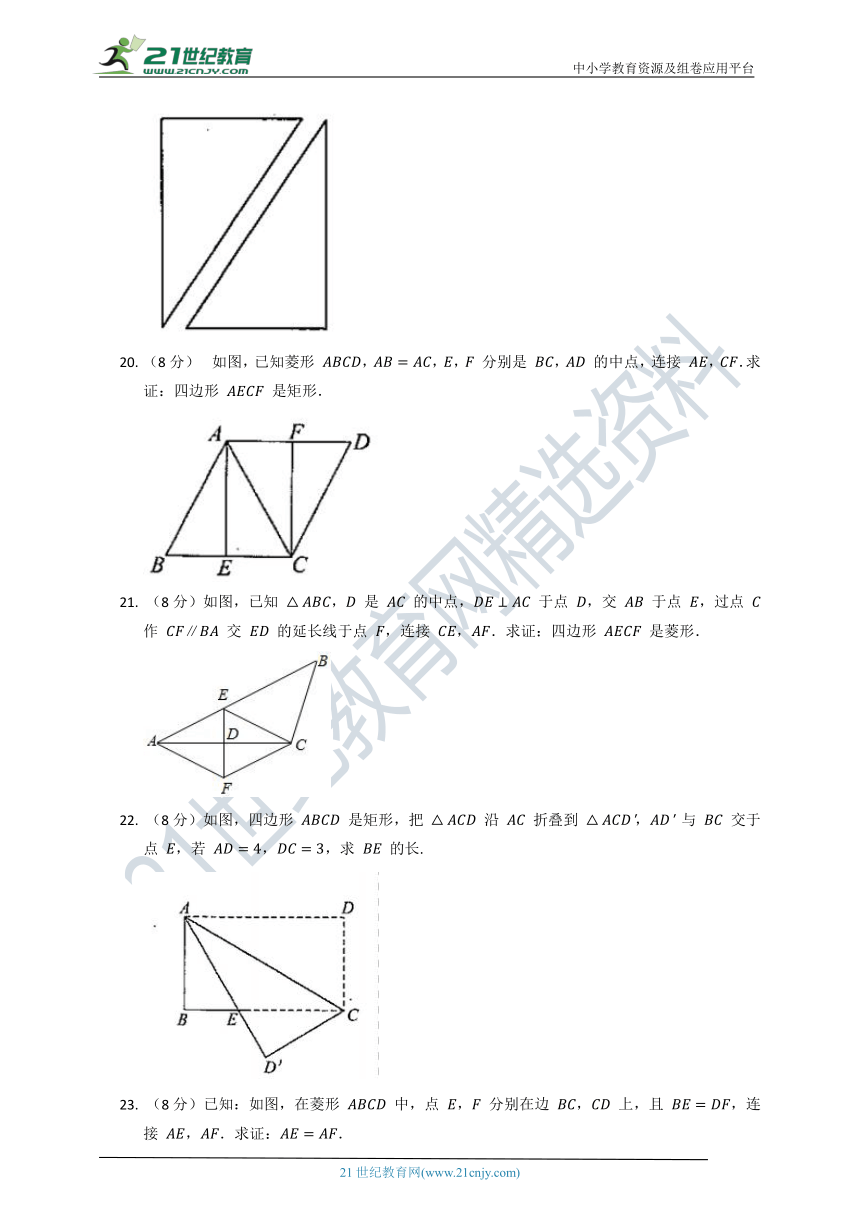
(8分)如图,把一张长方形纸片沿对角线剪开,得到两个完全相同的直角三角形,用这两个直角三角形你能拼出多少个形状不同的四边形?
20.
(8分)
如图,已知菱形
,,,
分别是
,
的中点,连接
,.求证:四边形
是矩形.
21.
(8分)如图,已知
,
是
的中点,
于点
,交
于点
,过点
作
交
的延长线于点
,连接
,.求证:四边形
是菱形.
22.
(8分)如图,四边形
是矩形,把
沿
折叠到
,
与
交于点
,若
,,求
的长.
23.
(8分)已知:如图,在菱形
中,点
,
分别在边
,
上,且
,连接
,.求证:.
24.
(8分)如图,在梯形
中,,,,,,
为
中点,
交
于点
,求
的长.
25.
(8分)正方形
的边长为
,正方形
的边长为
.
(1)如图①,求
的面积;
(2)如图②,若
为
的中点,求
的面积.
答案
第一部分
1.
D
2.
B
3.
D
【解析】
四边形
是菱形,,
,,
,
,
.
4.
A
【解析】B项,由
得
,
由
得
,
,
根据“两组对边分别平行的四边形为平行四边形”可以判定四边形
为平行四边形;
C项,根据“一组对边平行且相等的四边形是平行四边形”可以判定四边形
是平行四边形;
D项,由两组对角分别相等可得出两组对边分别平行,根据平行四边形的定义可以判定该四边形为平行四边形.
5.
A
6.
B
7.
D
【解析】
四边形
是平行四边形,
当
时,四边形
是菱形.
8.
C
【解析】,
.
.
9.
A
【解析】设
,,题图①中的平行四边形中相邻两条边的长是
,,,则
,
题图②中阴影部分的周长比题图③中阴影部分的周长大
,
,
解得
,
即
,,
所以
.
10.
D
【解析】作点
关于
的对称点
,连接
,交
于点
,作
,交
于点
,
点
,点
关于
对称,点
在
上,
,
,
的最小值为
的长,
四边形
为正方形,点
是
中点,
,,
,
.
第二部分
11.
,,
12.
①③④或②③④
13.
(答案不唯一)
【解析】由
,,可知四边形
有一个角是直角且一组邻边相等,如果四边形
是平行四边形,即可判定四边形
是正方形,
所以补充一个条件使四边形
是平行四边形即可.
14.
(答案不唯一)
【解析】答案不唯一.根据邻边相等的平行四边形是菱形,可添加
.
15.
两平行线间的距离处处相等
16.
第三部分
17.
,
.
,
,
,
.
为
边上的中线,,
,
,
.
18.
(1)
,
分别是
,
的中点,
,,
,
.
??????(2)
,
分别是
,
的中点,
,
,
.
19.
个.所拼成的四边形如图所示.
20.
,点
是
中点,
,
平行四边形
为菱形,
,
点
是
的中点,
且
,
四边形
为矩形.
21.
是
的中点,,
,,
,
,,
在
与
中,
,
,
为线段
的垂直平分线,
,
,
四边形
为菱形.
22.
四边形
为矩形,
,,,.
沿
折叠到
,
与
交于点
,
,
,
,
,
,
设
,则
,
在
中,
,
,
解得
,
即
的长为
.
23.
四边形
是蒌形,
,,
,
,
.
24.
过点
作
.
,
四边形
是平行四边形,
,
,
在
中,,
,
,
.
25.
(1)
如图
,连接
,
在正方形
和正方形
中,
,
,
分别平分
,,
,
,
与
同底等高,
.
??????(2)
如图
,连接
,,
由()知
,
点
为
的中点,
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
人教版2020-20201年八年级(下)第十八章平行四边形检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1.
观察下列各方格图中阴影部分所示的图形(每一小方格的边长为
),如果将它们沿方格边线或对角线剪开重新拼接,不能拼成正方形的是
A.
B.
C.
D.
2.
如图,在直角
的内部有一滑动杆
,当端点
沿直线
向下滑动时,端点
会随之自动地沿直线
向左滑动,如果滑动杆从图中
处滑动到
处,那么滑动杆的中点
所经过的路径是
A.
直线的一部分
B.
圆的一部分
C.
双曲线的一部分
D.
抛物线的一部分
3.
如图,菱形
中,,则
A.
B.
C.
D.
4.
下列不能判定四边形
为平行四边形的条件是
A.
,
B.
,
C.
,
D.
,
5.
下列关于矩形的对角线,有甲、乙两种说法:
甲:矩形的对角线互相平分;
乙:矩形的对角线相等.
对于这两种说法,下列判断正确的是
A.
甲、乙均正确
B.
甲错误,乙正确
C.
甲正确,乙错误
D.
甲、乙均错误
6.
梯形
中,,,,,,则
的长为
A.
B.
C.
D.
7.
下列条件中,能判定平行四边形
是菱形的是
A.
B.
C.
D.
8.
如图,在梯形
中,,,若
,则
的大小是
A.
B.
C.
D.
9.
如图,把六张大小形状完全相同的小平行四边形卡片放在一个底面为平行四边形的盒子底部,两种放置方法如图②,③所示,其中图③中的重叠部分是平行四边形
,若
,且图②中阴影部分的周长比图③中阴影部分的周长大
,则
的值为
A.
B.
C.
D.
10.
如图,在正方形
ABCD
中,
为
上的中点,
为
上的一个动点,若
,则
的最小值为
A.
B.
C.
D.
二、填空题(共6小题;每小题3分,共18分)
11.
判断题(正确的打“”,错误的打“”):
()有两个角相等的梯形是等腰梯形.
()如果梯形
中,,,,那么这个梯形是等腰梯形.
()如果梯形
中,,,那么这个梯形是等腰梯形.
12.
如图,在四边形
中,有以下四个条件;①
;②
;③
;④
.从中选取三个条件,可以判定四边形
为矩形,则可以选择的条件序号是
?.
13.
在四边形
中,,,试补充一个条件:
?,使四边形
是正方形.
14.
如图,平行四边形
的对角线
,
相交于点
,请添加一个条件:
?,使平行四边形
是菱形.
15.
木匠常用角尺在长方形表面上测量其宽度来判断是否平行,其中的原理是
?.
16.
如图所示,梯形
中,,,它恰好能按图示方式被分割成四个全等的直角梯形,如果
,那么
?.
三、解答题(共9小题;共72分)
17.(8分)
如图,在
中,,
于点
,
为
边上的中线.
求证:.
18.
(8分)
如图,在
中,,,
分别是
,
的中点,,垂足为
.求证:
(1);
(2).
19.
(8分)如图,把一张长方形纸片沿对角线剪开,得到两个完全相同的直角三角形,用这两个直角三角形你能拼出多少个形状不同的四边形?
20.
(8分)
如图,已知菱形
,,,
分别是
,
的中点,连接
,.求证:四边形
是矩形.
21.
(8分)如图,已知
,
是
的中点,
于点
,交
于点
,过点
作
交
的延长线于点
,连接
,.求证:四边形
是菱形.
22.
(8分)如图,四边形
是矩形,把
沿
折叠到
,
与
交于点
,若
,,求
的长.
23.
(8分)已知:如图,在菱形
中,点
,
分别在边
,
上,且
,连接
,.求证:.
24.
(8分)如图,在梯形
中,,,,,,
为
中点,
交
于点
,求
的长.
25.
(8分)正方形
的边长为
,正方形
的边长为
.
(1)如图①,求
的面积;
(2)如图②,若
为
的中点,求
的面积.
答案
第一部分
1.
D
2.
B
3.
D
【解析】
四边形
是菱形,,
,,
,
,
.
4.
A
【解析】B项,由
得
,
由
得
,
,
根据“两组对边分别平行的四边形为平行四边形”可以判定四边形
为平行四边形;
C项,根据“一组对边平行且相等的四边形是平行四边形”可以判定四边形
是平行四边形;
D项,由两组对角分别相等可得出两组对边分别平行,根据平行四边形的定义可以判定该四边形为平行四边形.
5.
A
6.
B
7.
D
【解析】
四边形
是平行四边形,
当
时,四边形
是菱形.
8.
C
【解析】,
.
.
9.
A
【解析】设
,,题图①中的平行四边形中相邻两条边的长是
,,,则
,
题图②中阴影部分的周长比题图③中阴影部分的周长大
,
,
解得
,
即
,,
所以
.
10.
D
【解析】作点
关于
的对称点
,连接
,交
于点
,作
,交
于点
,
点
,点
关于
对称,点
在
上,
,
,
的最小值为
的长,
四边形
为正方形,点
是
中点,
,,
,
.
第二部分
11.
,,
12.
①③④或②③④
13.
(答案不唯一)
【解析】由
,,可知四边形
有一个角是直角且一组邻边相等,如果四边形
是平行四边形,即可判定四边形
是正方形,
所以补充一个条件使四边形
是平行四边形即可.
14.
(答案不唯一)
【解析】答案不唯一.根据邻边相等的平行四边形是菱形,可添加
.
15.
两平行线间的距离处处相等
16.
第三部分
17.
,
.
,
,
,
.
为
边上的中线,,
,
,
.
18.
(1)
,
分别是
,
的中点,
,,
,
.
??????(2)
,
分别是
,
的中点,
,
,
.
19.
个.所拼成的四边形如图所示.
20.
,点
是
中点,
,
平行四边形
为菱形,
,
点
是
的中点,
且
,
四边形
为矩形.
21.
是
的中点,,
,,
,
,,
在
与
中,
,
,
为线段
的垂直平分线,
,
,
四边形
为菱形.
22.
四边形
为矩形,
,,,.
沿
折叠到
,
与
交于点
,
,
,
,
,
,
设
,则
,
在
中,
,
,
解得
,
即
的长为
.
23.
四边形
是蒌形,
,,
,
,
.
24.
过点
作
.
,
四边形
是平行四边形,
,
,
在
中,,
,
,
.
25.
(1)
如图
,连接
,
在正方形
和正方形
中,
,
,
分别平分
,,
,
,
与
同底等高,
.
??????(2)
如图
,连接
,,
由()知
,
点
为
的中点,
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
