人教版2020--2021八年级(下)数学第十八章《平行四边形》质量检测试卷B(含解析)
文档属性
| 名称 | 人教版2020--2021八年级(下)数学第十八章《平行四边形》质量检测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 08:51:02 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版2020-2021学年八年级(下)第十八章平行四边形检测试卷B
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
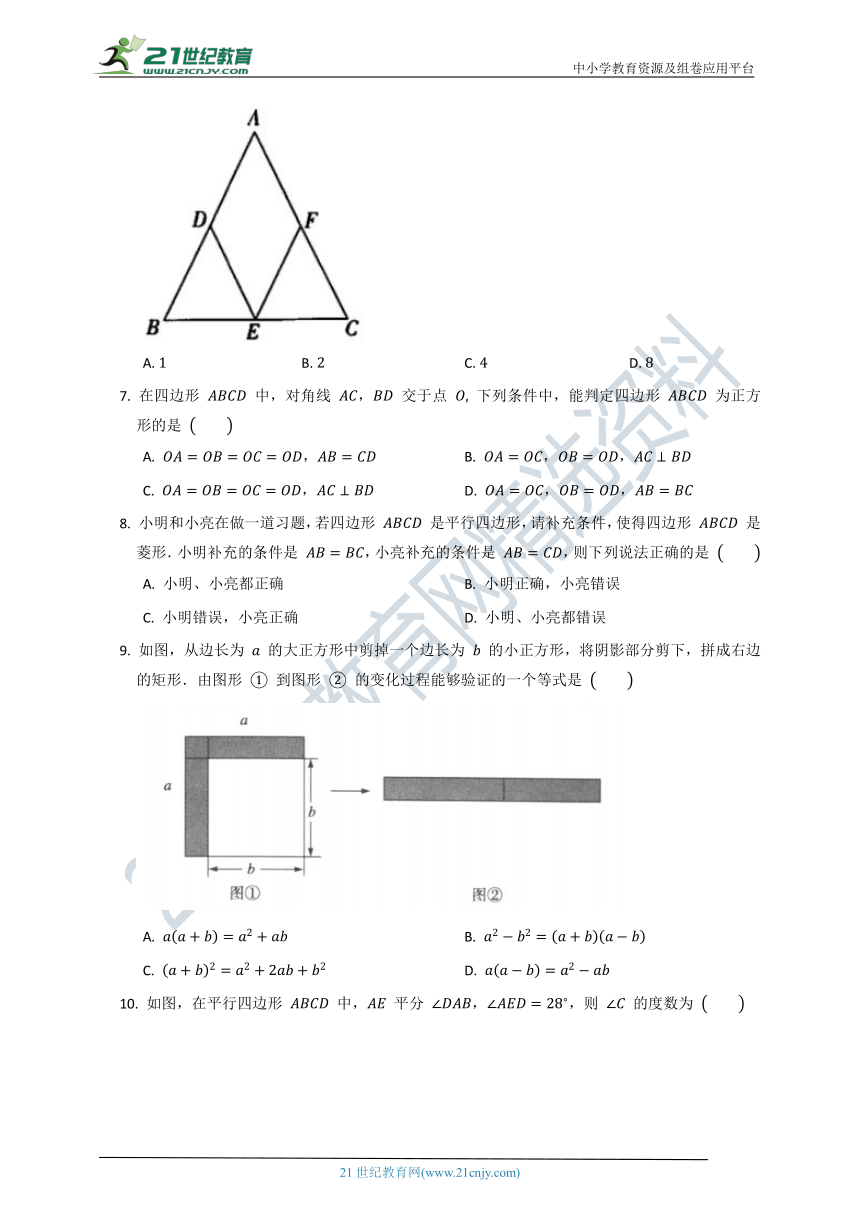
1.
如图,在
中,,点
是
的中点,,则
的长是
A.
B.
C.
D.
2.
下列说法正确的是
A.
有一组对边平行的四边形是梯形
B.
一组对边平行且不相等的四边形是梯形
C.
直角梯形是有两个角是直角的四边形
D.
有两个角相等的梯形是等腰梯形
3.
从①
;②
;③
;④
这四个条件中选取两个,使四边形
为平行四边形.下面不能说明四边形
是平行四边形的是
A.
①②
B.
①③
C.
②④
D.
①④
4.
如图所示的平行四边形
,再添加下列某一个条件,不能判定平行四边形
是矩形的是
A.
B.
C.
D.
5.
在同一平面内,设
,,
是三条互相平行的直线,已知
与
的距离为
,
与
的距离为
,则
与
的距离为
A.
B.
C.
或
D.
或
6.
如图,在
中,点
,,
分别是边
,,
的中点,若
,则四边形
的周长为
A.
B.
C.
D.
7.
在四边形
中,对角线
,
交于点
下列条件中,能判定四边形
为正方形的是
A.
,
B.
,,
C.
,
D.
,,
8.
小明和小亮在做一道习题,若四边形
是平行四边形,请补充条件,使得四边形
是菱形.小明补充的条件是
,小亮补充的条件是
,则下列说法正确的是
A.
小明、小亮都正确
B.
小明正确,小亮错误
C.
小明错误,小亮正确
D.
小明、小亮都错误
9.
如图,从边长为
的大正方形中剪掉一个边长为
的小正方形,将阴影部分剪下,拼成右边的矩形.由图形
到图形
的变化过程能够验证的一个等式是
A.
B.
C.
D.
10.
如图,在平行四边形
中,
平分
,,则
的度数为
A.
B.
C.
D.
二、填空题(共6小题;每小题3分,共18分)
11.
如图,在平行四边形
中,对角线
,
相交于点
,若再增加一个条件,就可得出平行四边形
是菱形,则你添加的条件是
?.
12.
已知菱形的一条对角线长为
,面积是
,则这个菱形的另一条对角线长是
?.
13.
在四边形
中,已知
,再添加一个条件,使得四边形
为正方形,可添加的条件是
?(写出一个即可).
14.
如图,两个阴影图形都是正方形,用两种方式表示这两个正方形的面积和,可以得到的等式为
?.
15.
已知梯形的两底长分别为
和
,两腰的长分别为
与
,那么字母
的取值范围为
?.
16.
已知直角梯形的一个锐角等于
,它两底分别为
厘米、
厘米,那么这个直角梯形的面积为
?平方厘米.
三、解答题(共9小题;共72分)
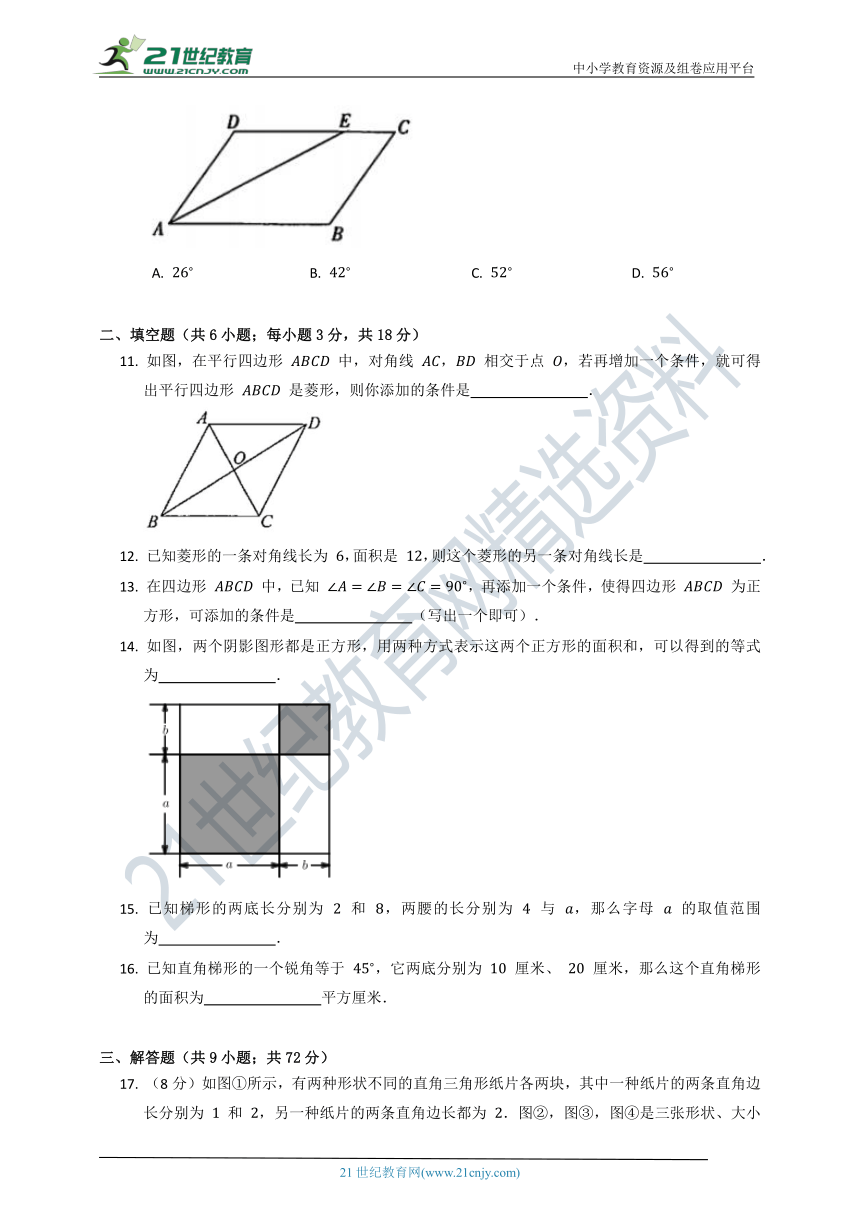
17.
(8分)如图①所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长分别为
和
,另一种纸片的两条直角边长都为
.图②,图③,图④是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为
.请用三种方法将图中所给的四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,三种方法所拼得的平行四边形(非矩形)的周长互不相等,并把你所拼得的图形分别画在图②,图③,图④的方格纸上.
要求:()所画图形各顶点必须与方格纸中的小正方形顶点重合;
()画图时,要保留四块直角三角形纸片的拼接痕迹.
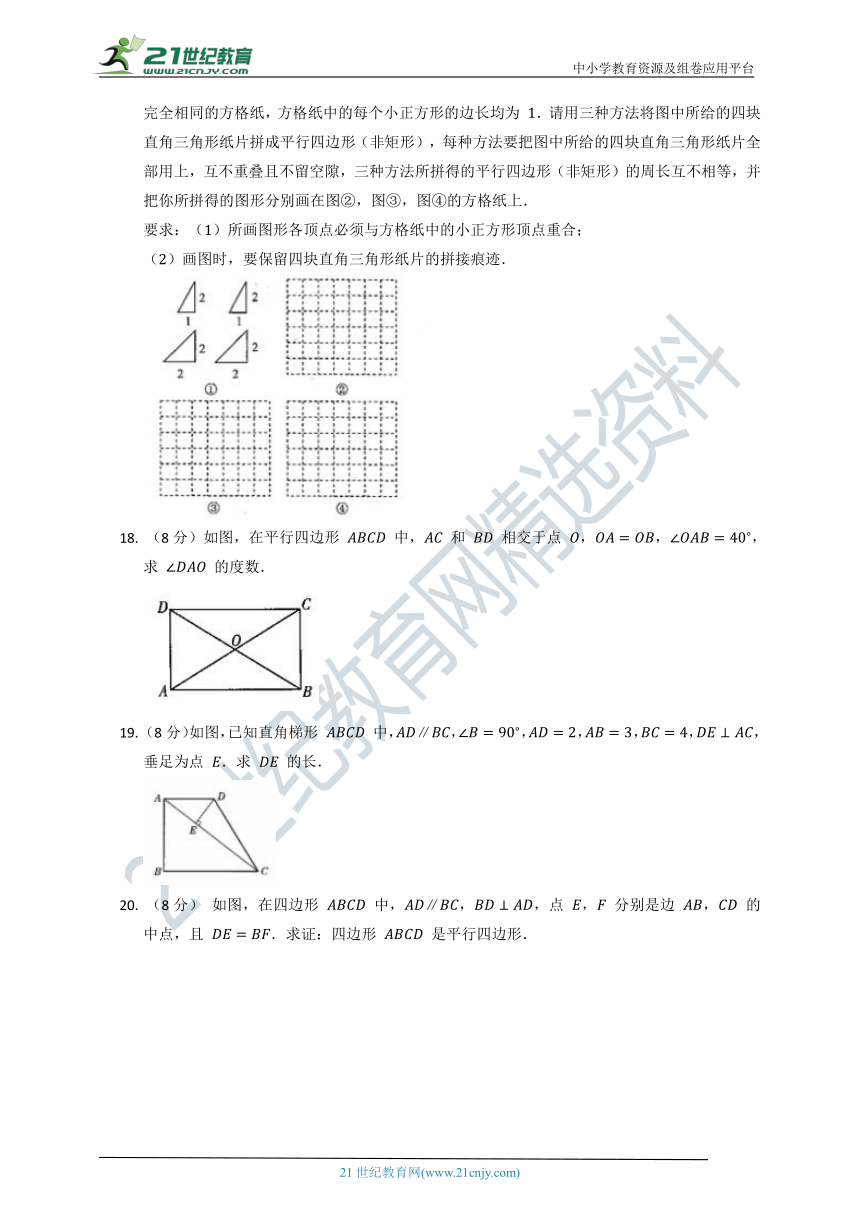
18.
(8分)如图,在平行四边形
中,
和
相交于点
,,,求
的度数.
19.
(8分)如图,已知直角梯形
中,,,,,,,垂足为点
.求
的长.
20.
(8分)
如图,在四边形
中,,,点
,
分别是边
,
的中点,且
.求证:四边形
是平行四边形.
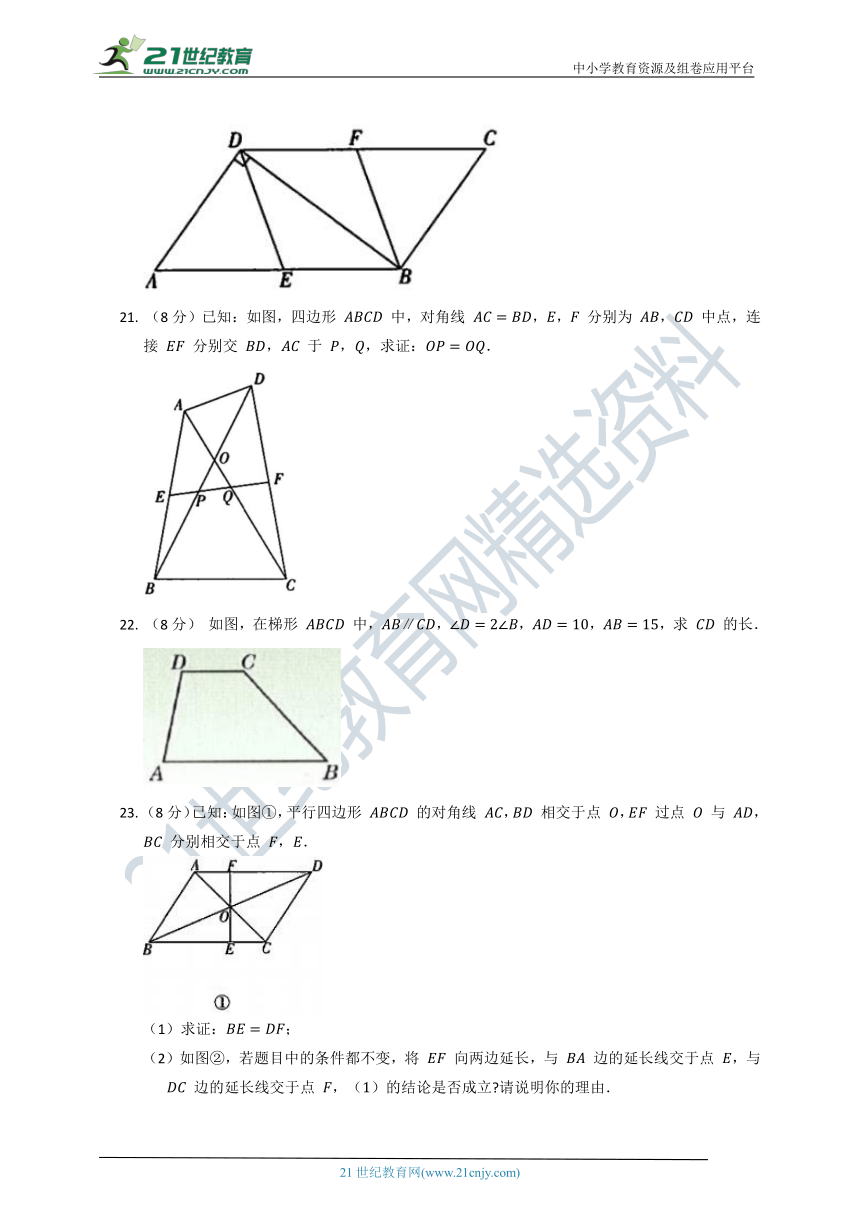
21.
(8分)已知:如图,四边形
中,对角线
,,
分别为
,
中点,连接
分别交
,
于
,,求证:.
22.
(8分)
如图,在梯形
中,,,,,求
的长.
23.
(8分)已知:如图①,平行四边形
的对角线
,
相交于点
,
过点
与
,
分别相交于点
,.
(1)求证:;
(2)如图②,若题目中的条件都不变,将
向两边延长,与
边的延长线交于点
,与
边的延长线交于点
,()的结论是否成立?请说明你的理由.
24.
(8分)如图,在矩形
中,,
分别是
,
的中点,,
分别交
于
,
两点.求证:
(1)四边形
是平行四边形.
(2).
25.
(8分)如图,正方形
的对角线
,
相交于点
,
是
上一点,连接
.过点
作
,垂足为
,
与
相交于点
.求证:.
答案
第一部分
1.
B
2.
B
3.
D
【解析】根据平行四边形的判定,符合条件的有
种,分别是①②,①③,②④,③④.
4.
C
【解析】根据对角线相等的平行四边形是矩形,可知
时,平行四边形
是矩形;
根据有一个角是直角的平行四边形是矩形,可知
时,平行四边形
是矩形;
在平行四边形
中,,
,
又
,
,
根据有一个角是直角的平行四边形是矩形,
可知
时,平行四边形
是矩形.
5.
C
【解析】当直线
在
,
之间时,
因为
,,
是三条互相平行的直线,
与
的距离为
,
与
的距离
,
所以
与
的距离为
();
当直线
不在
,
之间时,
因为
,,
是三条互相平行的直线,
与
的距离为
,
与
的距离为
,
所以
与
的距离为
().
综上所述,
与
的距离为
或
.
6.
C
【解析】
点
,,
分别是边
,,
的中点,
,,,
是
的中位线,
,,
四边形
的周长
.
7.
C
8.
B
9.
B
【解析】第一个图形阴影部分的面积是
,第二个图形的面积是
,则
.
10.
D
【解析】
四边形
为平行四边形,
,
,
平分
,
,
四边形
为平行四边形,
,
故选D.
第二部分
11.
12.
13.
答案不唯一,如
.
14.
【解析】用两种方式表示这两个正方形的面积,
方式一:两个小正方形的面积之和,即
.
方式二:大正方形面积减去两个长方形面积,即
,
可得到等式
.
15.
【解析】如图所示:
在梯形
中,,,,,,
作
交
于
,
则四边形
是平行四边形,
,,
,
在
中,由三角形的三边关系得:,
即
,
.
16.
第三部分
17.
如图.
18.
四边形
是平行四边形,
,.
,
.
四边形
是矩形.
.
,
.
19.
提示:用两种不同的方法表示
,可得
,所以
的长是
.
20.
,,
,
在
中,
是
的中点,
,同理得
,
,
,
在
和
中,
,
,
四边形
是平行四边形.
21.
如图,取
中点
,连接
,,
,
分别为
,
中点,
,,
,
同理,,,
,
,
,
,
,
.
22.
.
23.
(1)
四边形
是平行四边形,
,,
,
在
和
中,
,
.
??????(2)
成立.
理由:
四边形
是平行四边形,
,,
.
在
和
中,
,
.
24.
(1)
四边形
为矩形,
且
.
,
分别为
,
的中点,
且
.
四边形
为平行四边形.
??????(2)
,
,
.
又
,
.
.
,
.
.
25.
在正方形
中,
,,
,
,
四边形
为正方形,
,,,
,
在
和
中,
,
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
人教版2020-2021学年八年级(下)第十八章平行四边形检测试卷B
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1.
如图,在
中,,点
是
的中点,,则
的长是
A.
B.
C.
D.
2.
下列说法正确的是
A.
有一组对边平行的四边形是梯形
B.
一组对边平行且不相等的四边形是梯形
C.
直角梯形是有两个角是直角的四边形
D.
有两个角相等的梯形是等腰梯形
3.
从①
;②
;③
;④
这四个条件中选取两个,使四边形
为平行四边形.下面不能说明四边形
是平行四边形的是
A.
①②
B.
①③
C.
②④
D.
①④
4.
如图所示的平行四边形
,再添加下列某一个条件,不能判定平行四边形
是矩形的是
A.
B.
C.
D.
5.
在同一平面内,设
,,
是三条互相平行的直线,已知
与
的距离为
,
与
的距离为
,则
与
的距离为
A.
B.
C.
或
D.
或
6.
如图,在
中,点
,,
分别是边
,,
的中点,若
,则四边形
的周长为
A.
B.
C.
D.
7.
在四边形
中,对角线
,
交于点
下列条件中,能判定四边形
为正方形的是
A.
,
B.
,,
C.
,
D.
,,
8.
小明和小亮在做一道习题,若四边形
是平行四边形,请补充条件,使得四边形
是菱形.小明补充的条件是
,小亮补充的条件是
,则下列说法正确的是
A.
小明、小亮都正确
B.
小明正确,小亮错误
C.
小明错误,小亮正确
D.
小明、小亮都错误
9.
如图,从边长为
的大正方形中剪掉一个边长为
的小正方形,将阴影部分剪下,拼成右边的矩形.由图形
到图形
的变化过程能够验证的一个等式是
A.
B.
C.
D.
10.
如图,在平行四边形
中,
平分
,,则
的度数为
A.
B.
C.
D.
二、填空题(共6小题;每小题3分,共18分)
11.
如图,在平行四边形
中,对角线
,
相交于点
,若再增加一个条件,就可得出平行四边形
是菱形,则你添加的条件是
?.
12.
已知菱形的一条对角线长为
,面积是
,则这个菱形的另一条对角线长是
?.
13.
在四边形
中,已知
,再添加一个条件,使得四边形
为正方形,可添加的条件是
?(写出一个即可).
14.
如图,两个阴影图形都是正方形,用两种方式表示这两个正方形的面积和,可以得到的等式为
?.
15.
已知梯形的两底长分别为
和
,两腰的长分别为
与
,那么字母
的取值范围为
?.
16.
已知直角梯形的一个锐角等于
,它两底分别为
厘米、
厘米,那么这个直角梯形的面积为
?平方厘米.
三、解答题(共9小题;共72分)
17.
(8分)如图①所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长分别为
和
,另一种纸片的两条直角边长都为
.图②,图③,图④是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为
.请用三种方法将图中所给的四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,三种方法所拼得的平行四边形(非矩形)的周长互不相等,并把你所拼得的图形分别画在图②,图③,图④的方格纸上.
要求:()所画图形各顶点必须与方格纸中的小正方形顶点重合;
()画图时,要保留四块直角三角形纸片的拼接痕迹.
18.
(8分)如图,在平行四边形
中,
和
相交于点
,,,求
的度数.
19.
(8分)如图,已知直角梯形
中,,,,,,,垂足为点
.求
的长.
20.
(8分)
如图,在四边形
中,,,点
,
分别是边
,
的中点,且
.求证:四边形
是平行四边形.
21.
(8分)已知:如图,四边形
中,对角线
,,
分别为
,
中点,连接
分别交
,
于
,,求证:.
22.
(8分)
如图,在梯形
中,,,,,求
的长.
23.
(8分)已知:如图①,平行四边形
的对角线
,
相交于点
,
过点
与
,
分别相交于点
,.
(1)求证:;
(2)如图②,若题目中的条件都不变,将
向两边延长,与
边的延长线交于点
,与
边的延长线交于点
,()的结论是否成立?请说明你的理由.
24.
(8分)如图,在矩形
中,,
分别是
,
的中点,,
分别交
于
,
两点.求证:
(1)四边形
是平行四边形.
(2).
25.
(8分)如图,正方形
的对角线
,
相交于点
,
是
上一点,连接
.过点
作
,垂足为
,
与
相交于点
.求证:.
答案
第一部分
1.
B
2.
B
3.
D
【解析】根据平行四边形的判定,符合条件的有
种,分别是①②,①③,②④,③④.
4.
C
【解析】根据对角线相等的平行四边形是矩形,可知
时,平行四边形
是矩形;
根据有一个角是直角的平行四边形是矩形,可知
时,平行四边形
是矩形;
在平行四边形
中,,
,
又
,
,
根据有一个角是直角的平行四边形是矩形,
可知
时,平行四边形
是矩形.
5.
C
【解析】当直线
在
,
之间时,
因为
,,
是三条互相平行的直线,
与
的距离为
,
与
的距离
,
所以
与
的距离为
();
当直线
不在
,
之间时,
因为
,,
是三条互相平行的直线,
与
的距离为
,
与
的距离为
,
所以
与
的距离为
().
综上所述,
与
的距离为
或
.
6.
C
【解析】
点
,,
分别是边
,,
的中点,
,,,
是
的中位线,
,,
四边形
的周长
.
7.
C
8.
B
9.
B
【解析】第一个图形阴影部分的面积是
,第二个图形的面积是
,则
.
10.
D
【解析】
四边形
为平行四边形,
,
,
平分
,
,
四边形
为平行四边形,
,
故选D.
第二部分
11.
12.
13.
答案不唯一,如
.
14.
【解析】用两种方式表示这两个正方形的面积,
方式一:两个小正方形的面积之和,即
.
方式二:大正方形面积减去两个长方形面积,即
,
可得到等式
.
15.
【解析】如图所示:
在梯形
中,,,,,,
作
交
于
,
则四边形
是平行四边形,
,,
,
在
中,由三角形的三边关系得:,
即
,
.
16.
第三部分
17.
如图.
18.
四边形
是平行四边形,
,.
,
.
四边形
是矩形.
.
,
.
19.
提示:用两种不同的方法表示
,可得
,所以
的长是
.
20.
,,
,
在
中,
是
的中点,
,同理得
,
,
,
在
和
中,
,
,
四边形
是平行四边形.
21.
如图,取
中点
,连接
,,
,
分别为
,
中点,
,,
,
同理,,,
,
,
,
,
,
.
22.
.
23.
(1)
四边形
是平行四边形,
,,
,
在
和
中,
,
.
??????(2)
成立.
理由:
四边形
是平行四边形,
,,
.
在
和
中,
,
.
24.
(1)
四边形
为矩形,
且
.
,
分别为
,
的中点,
且
.
四边形
为平行四边形.
??????(2)
,
,
.
又
,
.
.
,
.
.
25.
在正方形
中,
,,
,
,
四边形
为正方形,
,,,
,
在
和
中,
,
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
