鲁教版(五四制)八年级下册数学 7.1二次根式 课件(15张ppt)
文档属性
| 名称 | 鲁教版(五四制)八年级下册数学 7.1二次根式 课件(15张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 914.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 15:20:25 | ||
图片预览






文档简介
一般地,如果一个正数的平方等于a,那么这个正数叫做a的算术平方根,记作“ ”。
2.求下列各数的算术平方根。
(1) 7 (2) 0 (3) -5 (4)
0
正数的算术平方根是正数,0的算术平方根是0,负数没有算术平方根.
复习巩固
1.什么叫做算术平方根?
学习目标
1.理解二次根式的概念,会判断一个式子是否
是二次根式.
2.掌握二次根式有意义的条件.
3.理解 ,并能进行相关的计算.
4.通过二次根式的计算锻炼逻辑思维能力。
)
0
(
)
(
2
≥
=
a
a
a
学习重难点:
1.二次根式的意义。
2.确定二次根式中字母的取值范围。
合作探究:
完成下列题目:
探究一:二次根式的概念
合作探究
1.正方形的面积为2,它的边长是 ,面积为3的正方形边长是 ;
2.面积为S的正方形边长是 ,把它的面积增加1,新正方形的边长为 ;
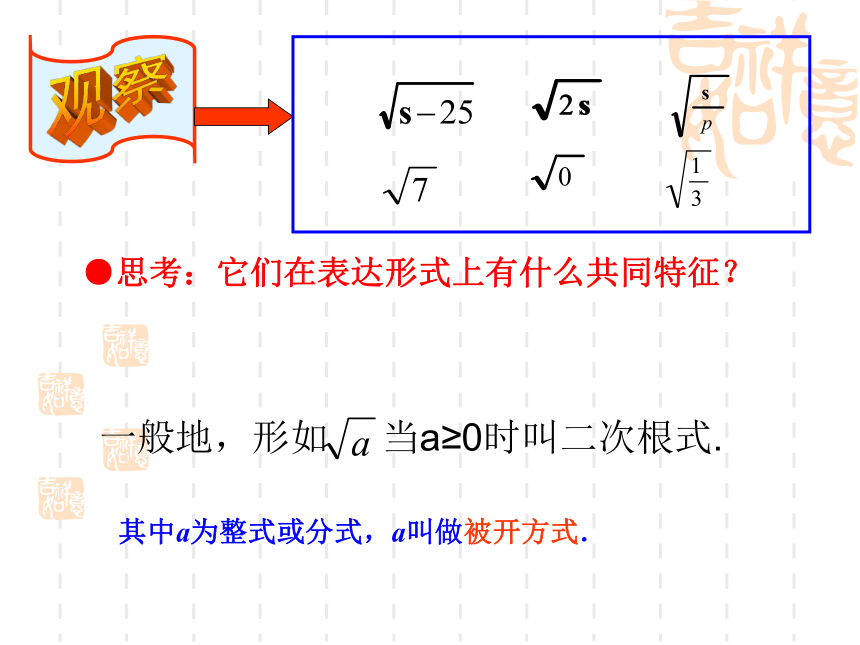
●思考:它们在表达形式上有什么共同特征?
一般地,形如 当a≥0时叫二次根式.
其中a为整式或分式,a叫做被开方式.
小组合作:二次根式必需具备哪些条件?
(1)含有二次根号 .
(2)被开方式是一个非负数.
练习一:
1.下列各式中哪些是二次根式?并说明理由.
√
√
(4) (5) (6)
(1) (2) (3)
X
X
X
X
2、下列各式中哪些是二次根式?并说明理由.
√
√
√
例1
探究二:二次根式有意义的条件。
(1)
(2)
a是怎样的实数时,下列各式在实数范围内有意义?
(3)
练习一:
当 分别取什么实数时,下列各式有意义?
1
x
①被开方式是一个非负数;
②分母中有字母时,要保证分母不为零.
●思考:二次根式有意义的条件?
小组合作
4
6
0
a
探究三:二次根式的性质。
一个非负数的算术平方根的平方等于这个非负数.
)
0
(
)
(
2
≥
=
a
a
a
(a≥0)
例2
计算:
练习一:
计算:
)
5
4
)(
4
(
2
)
1
)(
5
(
2
+
x2
通过这节课的学习,你有哪些收获?
二次根式和
它的性质
概念
有意义的条件
性质
(1)一般地,形如 ( a≥0 ) 的式子叫做二次根式.
(2)条件
(1)含有二次根号 。
(2)被开方式是一个非负数。
(1)被开方式是一个非负数;
(2)分母中有字母时,要保证分母
不为零.
课堂小结
)
0
(
)
(
2
≥
=
a
a
a
谢谢观看
2.求下列各数的算术平方根。
(1) 7 (2) 0 (3) -5 (4)
0
正数的算术平方根是正数,0的算术平方根是0,负数没有算术平方根.
复习巩固
1.什么叫做算术平方根?
学习目标
1.理解二次根式的概念,会判断一个式子是否
是二次根式.
2.掌握二次根式有意义的条件.
3.理解 ,并能进行相关的计算.
4.通过二次根式的计算锻炼逻辑思维能力。
)
0
(
)
(
2
≥
=
a
a
a
学习重难点:
1.二次根式的意义。
2.确定二次根式中字母的取值范围。
合作探究:
完成下列题目:
探究一:二次根式的概念
合作探究
1.正方形的面积为2,它的边长是 ,面积为3的正方形边长是 ;
2.面积为S的正方形边长是 ,把它的面积增加1,新正方形的边长为 ;
●思考:它们在表达形式上有什么共同特征?
一般地,形如 当a≥0时叫二次根式.
其中a为整式或分式,a叫做被开方式.
小组合作:二次根式必需具备哪些条件?
(1)含有二次根号 .
(2)被开方式是一个非负数.
练习一:
1.下列各式中哪些是二次根式?并说明理由.
√
√
(4) (5) (6)
(1) (2) (3)
X
X
X
X
2、下列各式中哪些是二次根式?并说明理由.
√
√
√
例1
探究二:二次根式有意义的条件。
(1)
(2)
a是怎样的实数时,下列各式在实数范围内有意义?
(3)
练习一:
当 分别取什么实数时,下列各式有意义?
1
x
①被开方式是一个非负数;
②分母中有字母时,要保证分母不为零.
●思考:二次根式有意义的条件?
小组合作
4
6
0
a
探究三:二次根式的性质。
一个非负数的算术平方根的平方等于这个非负数.
)
0
(
)
(
2
≥
=
a
a
a
(a≥0)
例2
计算:
练习一:
计算:
)
5
4
)(
4
(
2
)
1
)(
5
(
2
+
x2
通过这节课的学习,你有哪些收获?
二次根式和
它的性质
概念
有意义的条件
性质
(1)一般地,形如 ( a≥0 ) 的式子叫做二次根式.
(2)条件
(1)含有二次根号 。
(2)被开方式是一个非负数。
(1)被开方式是一个非负数;
(2)分母中有字母时,要保证分母
不为零.
课堂小结
)
0
(
)
(
2
≥
=
a
a
a
谢谢观看
