苏科版七年级下册数学课件 7.7小结与思考(共16张ppt)
文档属性
| 名称 | 苏科版七年级下册数学课件 7.7小结与思考(共16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 783.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 19:35:01 | ||
图片预览


文档简介
第7章 小结与思考1
1.平行线的判定与性质
在同一平面上,两条直线的位置关系有 或者 。
对顶角 。同角或 的余角 ;同角或 的 相等。
判定与性质:
什么叫做平行线?在同一平面上, 的两直线叫平行线。
的两直线平行。
平行线的判定
1.同位角相等,两直线平行。
2.内错角相等,两直线平行。
3.同旁内角互补,两直线平行。
平行线的性质
1.两直线平行,同位角相等。
2.两直线平行,内错角相等 。
3.两直线平行,同旁内角互补。
C/
B/
A/
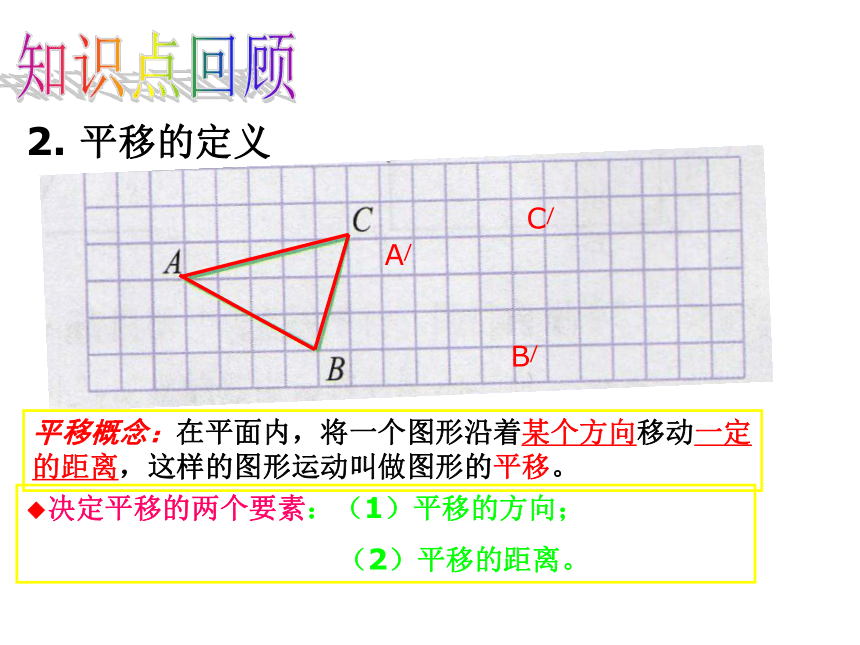
2. 平移的定义
平移概念:在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移。
◆决定平移的两个要素:(1)平移的方向;
(2)平移的距离。
(1)平移不改变图形的形状、大小,只改变图形的位置。
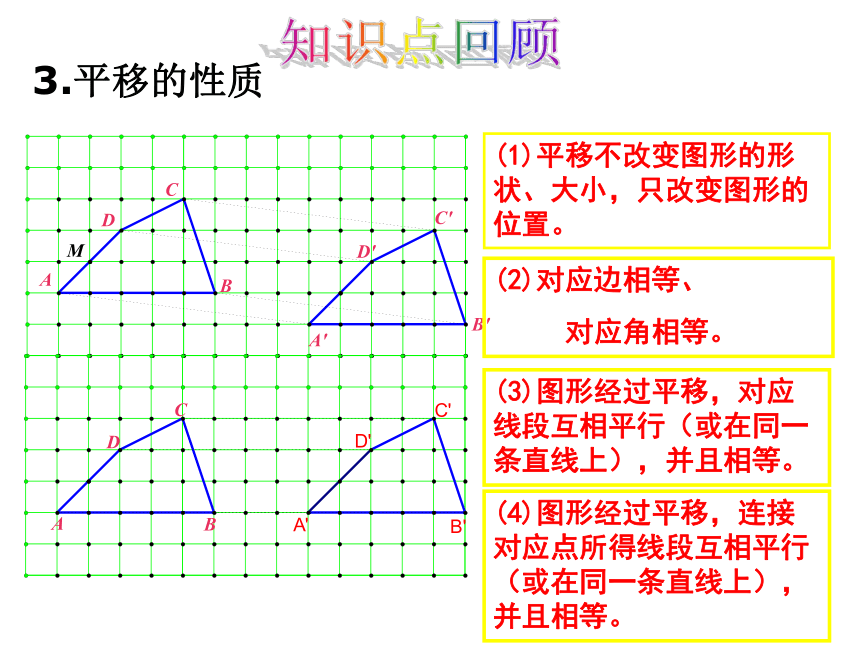
3.平移的性质
(2)对应边相等、
对应角相等。
(3)图形经过平移,对应线段互相平行(或在同一条直线上),并且相等。
(4)图形经过平移,连接对应点所得线段互相平行(或在同一条直线上),并且相等。
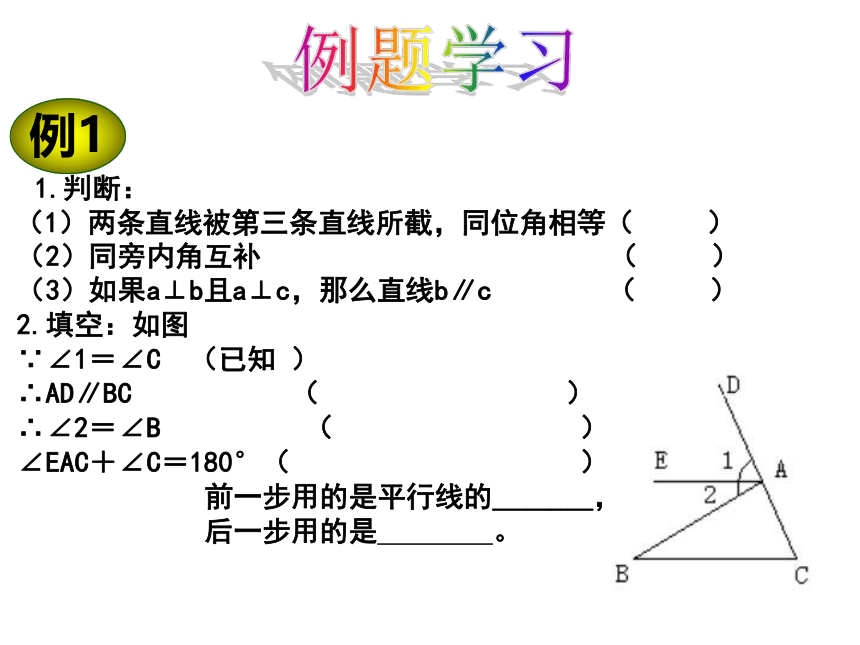
例1
判断:
(1)两条直线被第三条直线所截,同位角相等( )
(2)同旁内角互补 ( )
(3)如果a⊥b且a⊥c,那么直线b∥c ( )
2.填空:如图
∵∠1=∠C (已知 )
∴AD∥BC ( )
∴∠2=∠B ( )
∠EAC+∠C=180°( )
前一步用的是平行线的_______,
后一步用的是 。
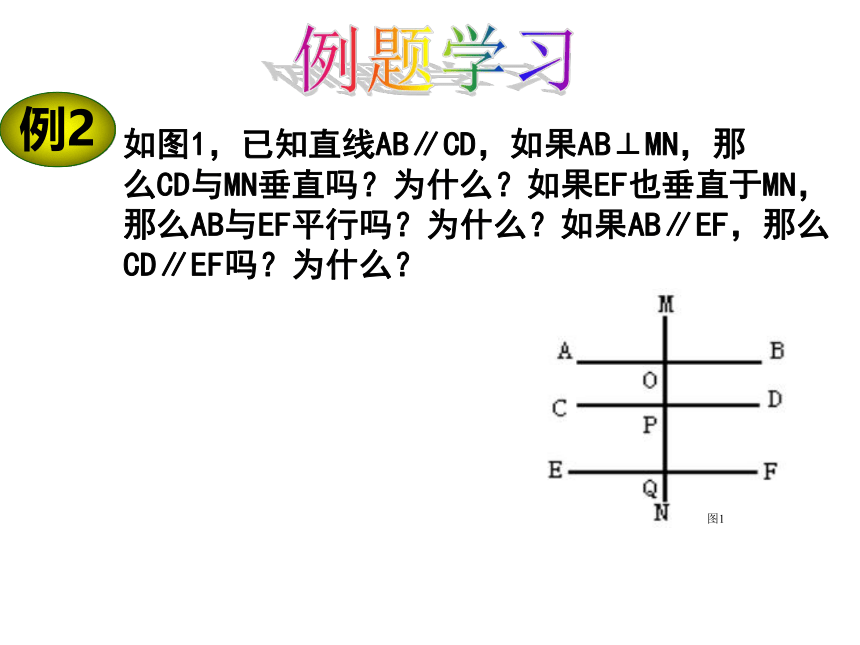
例2
图1
如图1,已知直线AB∥CD,如果AB⊥MN,那
么CD与MN垂直吗?为什么?如果EF也垂直于MN,
那么AB与EF平行吗?为什么?如果AB∥EF,那么
CD∥EF吗?为什么?
例3
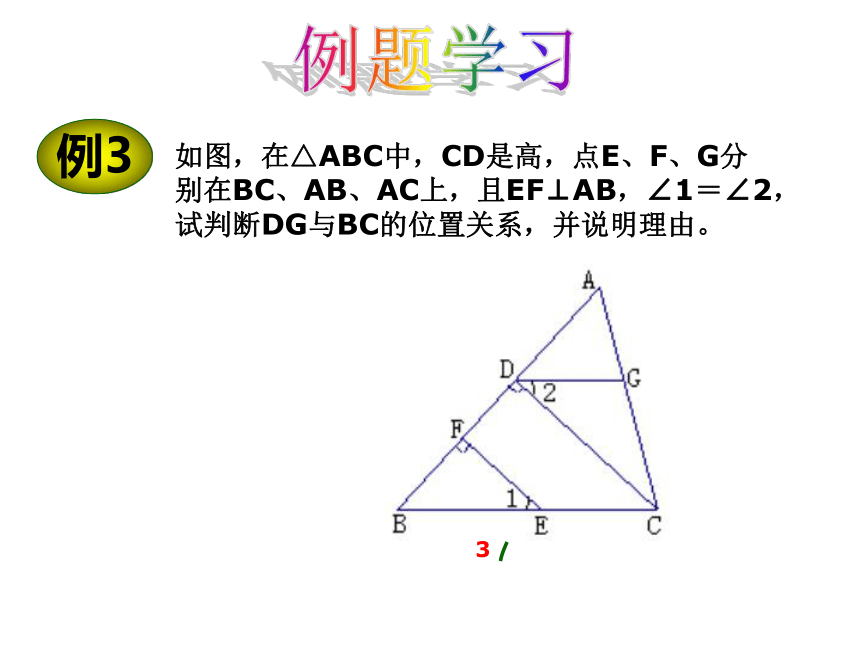
如图,在△ABC中,CD是高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由。
3
例4
A
B
D
C
E
F
如下图,面积为12cm2的△ABC沿BC方向平移至
△DEF位置,平移的距离是BC的三倍,则图中四边形
ACED的面积为 .
例5
已知,如图,AC∥DE,CD∥EF,
试说明:∠1=∠2
3
例6
已知,如图,AB∥CD,∠BAC、∠ACD的
平分线相交于点E,试求∠E的度数。
1
在A、B两地之间修一条笔直的公路,从A地测得公路的走向为北偏东60,如果A、B两地同时开工,那么∠α是多少度时,才能使公路准确接通?
0
2
如图,一块钢板ABCD的两边AB、CD平行,要在AB上找一点E,使∠AEC=150,应怎样确定点E的位置?为什么?
0
E
3
如图,∠1=∠2,∠3=100,则∠4=
0
4
如图,EG∥AB,FG∥DC,∠B=100,
∠C =120,则 ∠EGF =
0
0
100
0
120
0
80
0
60
0
5
0
如图,AB∥CD,∠B=120,∠D=130,
求∠BED的度数。
0
F
1
2
拓展
如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
F
1
2
1.平行线的判定与性质
在同一平面上,两条直线的位置关系有 或者 。
对顶角 。同角或 的余角 ;同角或 的 相等。
判定与性质:
什么叫做平行线?在同一平面上, 的两直线叫平行线。
的两直线平行。
平行线的判定
1.同位角相等,两直线平行。
2.内错角相等,两直线平行。
3.同旁内角互补,两直线平行。
平行线的性质
1.两直线平行,同位角相等。
2.两直线平行,内错角相等 。
3.两直线平行,同旁内角互补。
C/
B/
A/
2. 平移的定义
平移概念:在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移。
◆决定平移的两个要素:(1)平移的方向;
(2)平移的距离。
(1)平移不改变图形的形状、大小,只改变图形的位置。
3.平移的性质
(2)对应边相等、
对应角相等。
(3)图形经过平移,对应线段互相平行(或在同一条直线上),并且相等。
(4)图形经过平移,连接对应点所得线段互相平行(或在同一条直线上),并且相等。
例1
判断:
(1)两条直线被第三条直线所截,同位角相等( )
(2)同旁内角互补 ( )
(3)如果a⊥b且a⊥c,那么直线b∥c ( )
2.填空:如图
∵∠1=∠C (已知 )
∴AD∥BC ( )
∴∠2=∠B ( )
∠EAC+∠C=180°( )
前一步用的是平行线的_______,
后一步用的是 。
例2
图1
如图1,已知直线AB∥CD,如果AB⊥MN,那
么CD与MN垂直吗?为什么?如果EF也垂直于MN,
那么AB与EF平行吗?为什么?如果AB∥EF,那么
CD∥EF吗?为什么?
例3
如图,在△ABC中,CD是高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由。
3
例4
A
B
D
C
E
F
如下图,面积为12cm2的△ABC沿BC方向平移至
△DEF位置,平移的距离是BC的三倍,则图中四边形
ACED的面积为 .
例5
已知,如图,AC∥DE,CD∥EF,
试说明:∠1=∠2
3
例6
已知,如图,AB∥CD,∠BAC、∠ACD的
平分线相交于点E,试求∠E的度数。
1
在A、B两地之间修一条笔直的公路,从A地测得公路的走向为北偏东60,如果A、B两地同时开工,那么∠α是多少度时,才能使公路准确接通?
0
2
如图,一块钢板ABCD的两边AB、CD平行,要在AB上找一点E,使∠AEC=150,应怎样确定点E的位置?为什么?
0
E
3
如图,∠1=∠2,∠3=100,则∠4=
0
4
如图,EG∥AB,FG∥DC,∠B=100,
∠C =120,则 ∠EGF =
0
0
100
0
120
0
80
0
60
0
5
0
如图,AB∥CD,∠B=120,∠D=130,
求∠BED的度数。
0
F
1
2
拓展
如图,AB∥CD, 试找出∠BED 、∠B、∠D之间的关系。
F
1
2
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
