苏科版八年级下册数学 11.2反比例函数的图象与性质 课件(共23张ppt)
文档属性
| 名称 | 苏科版八年级下册数学 11.2反比例函数的图象与性质 课件(共23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 19:43:08 | ||
图片预览







文档简介
数学苏课版八年级(下)
——创设情境,回顾复习:
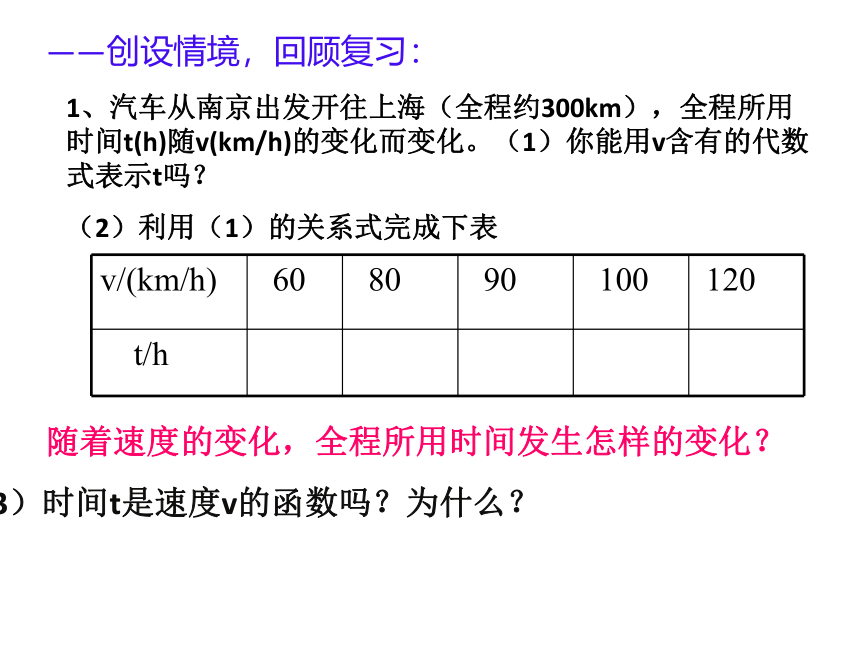
1、汽车从南京出发开往上海(全程约300km),全程所用时间t(h)随v(km/h)的变化而变化。(1)你能用v含有的代数式表示t吗?
(2)利用(1)的关系式完成下表
v/(km/h)
60
80
90
100
120
t/h
随着速度的变化,全程所用时间发生怎样的变化?
(3)时间t是速度v的函数吗?为什么?
1、当路程s一定时,时间t与速度v的函数关
系;
2、当矩形面积S一定时,长a与宽b的函数关
系:
3、当三角形面积S一定时,三角形的底边y
与高x的函数关系;
4、当功W一定时,力F与物体在力的方向上
通过的距离s的函数关系。
下列问题中,变量间都成反比例关系,请从函数角度出发,写出下列函数关系式。
------建立反比例函数模型:
------常见反比例函数模型:
1、当路程s一定时,时间t与速度v的函数关
系;
2、当矩形面积S一定时,长a与宽b的函数关
系:
3、当三角形面积S一定时,三角形的底边y
与高x的函数关系;
4、当功W一定时,力F与物体在力的方向上
通过的距离s的函数关系。
t= — (s是常数)
a= — (S是常数)
y= — (S是常数)
F= — (W是常数)
s
v
S
b
S
x
W
s
一般地,函数y= ? (k是常数,k≠ 0)叫做反比例函数.
x
k
反比例函数的五种不同的表现形式
归纳总结
形式1:y 是 x 反比例函数
形式2:y = (k为常数,k≠0)
形式3:y = kx-1 (k为常数,k≠0)
形式4:xy = k (k为常数,k≠0)
形式5:变量 y 与 x 成反比例,比例系数为k(k≠0)
------学习新课,研究函数图像
根据一次函数学习特殊函数的经验,研究完函数的概念,接着需要研究什么?
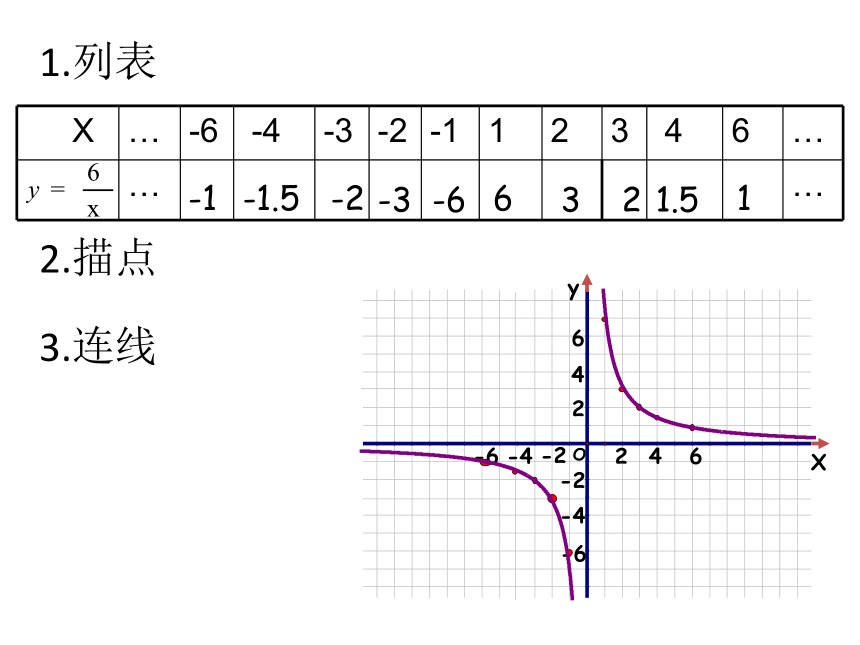
例1、画出反比例函数 和 的图象。
——探索归纳图像性质
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
X
…
-6
-4
-3
-2
-1
1
2
3
4
6
…
…
…
1.列表
2.描点
-1
-1.5
-2
-3
-6
6
3
2
1.5
1
3.连线
自主展示
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
说一说反比例函数 的图象与一次函数 的图象有什么区别?
自主拓展
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
1.通过比较反比例函数 与 的图象的特征,说出它们相同点与不同点?
一般地反比例函数 (k为常
数,k≠0) 的图象是由两个分支组成的,叫做双
曲线.
反比例函数的图象:
画出反比例函数y=-
和y=-- 的图象。
x
5
5
x
它们的共同特征以及不同点是什么?
每个函数的图象分别位于哪几个象限?
所在象限与什么有关?
在每一象限内,y随x的变化如何变化?
探索反比例函数的性质
y=-
x
5
y=--
x
5
从表格上看,当x的值从小到大变化时,y的值也从小到大或从大到小变化;
从解析式看,因为k>0,所以x与y同号,图象在一、三象限;因为k<0,所以x与y异号,图象在二、四象限;
从图象上看,图象在一、三象限时,y随x增大而减小;图象在二、四象限时,y随x增大而增大。
一定要注意:在每个象限内。
(第1题) (第2题)
1)、已知反比例函数y=-的图象如图所示,则k____0,
在图象的每一支上,y随x的增大而____;
2)、已知反比例函数y=--的图象如图所示,则k____0,
在图象的每一支上,y随x的 增大而____.
——应用拓展
x
2
2
x
2、右图是反比例函数
的图象的一支,
根据图象回答 下列问题:
(1)图象的另一支在哪个象限, 常数n的取值范围是什么?
(2)在图象上任取点A(a,b )和点B(a?,b?),如果a——应用拓展(2)
1、甲乙两地相距100km,一辆火车从甲地开往乙地,
把火车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )
C
自主拓展
设函数y=(m-2) .
(1)当m取何值时,它是反比例函数?(2)画出它的图象;
(3)利用图象,求当 ≤x≤2时,函数y的取值范围.
C
自主拓展——综合
进一步尝试:
在函数y=- , y=-x+5, y=2x的图象中,是中心对称图形且对称中心是原点的是____
动动脑筋:
在一个反比例函数图象上任取两点P、Q,过P、 Q两点分别作x轴、y轴的平行线(或垂线),与坐 标轴围成的矩形面积为S1和S2,那么S1与S2有什么 大小关系?
x
2
我学会了_______________
我认识到_______________
我有困惑_______________
课后思考:
(1)为什么反比例函数图象与x轴
(2)在一个反比例函数图象上任取点P,过P点分别作x轴、y轴的平行线(或垂线),与坐 标轴围成的矩形面积为S,与k有什么关系?
y轴无限接近却永不相交?
——创设情境,回顾复习:
1、汽车从南京出发开往上海(全程约300km),全程所用时间t(h)随v(km/h)的变化而变化。(1)你能用v含有的代数式表示t吗?
(2)利用(1)的关系式完成下表
v/(km/h)
60
80
90
100
120
t/h
随着速度的变化,全程所用时间发生怎样的变化?
(3)时间t是速度v的函数吗?为什么?
1、当路程s一定时,时间t与速度v的函数关
系;
2、当矩形面积S一定时,长a与宽b的函数关
系:
3、当三角形面积S一定时,三角形的底边y
与高x的函数关系;
4、当功W一定时,力F与物体在力的方向上
通过的距离s的函数关系。
下列问题中,变量间都成反比例关系,请从函数角度出发,写出下列函数关系式。
------建立反比例函数模型:
------常见反比例函数模型:
1、当路程s一定时,时间t与速度v的函数关
系;
2、当矩形面积S一定时,长a与宽b的函数关
系:
3、当三角形面积S一定时,三角形的底边y
与高x的函数关系;
4、当功W一定时,力F与物体在力的方向上
通过的距离s的函数关系。
t= — (s是常数)
a= — (S是常数)
y= — (S是常数)
F= — (W是常数)
s
v
S
b
S
x
W
s
一般地,函数y= ? (k是常数,k≠ 0)叫做反比例函数.
x
k
反比例函数的五种不同的表现形式
归纳总结
形式1:y 是 x 反比例函数
形式2:y = (k为常数,k≠0)
形式3:y = kx-1 (k为常数,k≠0)
形式4:xy = k (k为常数,k≠0)
形式5:变量 y 与 x 成反比例,比例系数为k(k≠0)
------学习新课,研究函数图像
根据一次函数学习特殊函数的经验,研究完函数的概念,接着需要研究什么?
例1、画出反比例函数 和 的图象。
——探索归纳图像性质
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
X
…
-6
-4
-3
-2
-1
1
2
3
4
6
…
…
…
1.列表
2.描点
-1
-1.5
-2
-3
-6
6
3
2
1.5
1
3.连线
自主展示
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
说一说反比例函数 的图象与一次函数 的图象有什么区别?
自主拓展
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
O
X
y
2
4
6
-2
-4
-6
2
4
6
-2
-4
-6
1.通过比较反比例函数 与 的图象的特征,说出它们相同点与不同点?
一般地反比例函数 (k为常
数,k≠0) 的图象是由两个分支组成的,叫做双
曲线.
反比例函数的图象:
画出反比例函数y=-
和y=-- 的图象。
x
5
5
x
它们的共同特征以及不同点是什么?
每个函数的图象分别位于哪几个象限?
所在象限与什么有关?
在每一象限内,y随x的变化如何变化?
探索反比例函数的性质
y=-
x
5
y=--
x
5
从表格上看,当x的值从小到大变化时,y的值也从小到大或从大到小变化;
从解析式看,因为k>0,所以x与y同号,图象在一、三象限;因为k<0,所以x与y异号,图象在二、四象限;
从图象上看,图象在一、三象限时,y随x增大而减小;图象在二、四象限时,y随x增大而增大。
一定要注意:在每个象限内。
(第1题) (第2题)
1)、已知反比例函数y=-的图象如图所示,则k____0,
在图象的每一支上,y随x的增大而____;
2)、已知反比例函数y=--的图象如图所示,则k____0,
在图象的每一支上,y随x的 增大而____.
——应用拓展
x
2
2
x
2、右图是反比例函数
的图象的一支,
根据图象回答 下列问题:
(1)图象的另一支在哪个象限, 常数n的取值范围是什么?
(2)在图象上任取点A(a,b )和点B(a?,b?),如果a
1、甲乙两地相距100km,一辆火车从甲地开往乙地,
把火车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )
C
自主拓展
设函数y=(m-2) .
(1)当m取何值时,它是反比例函数?(2)画出它的图象;
(3)利用图象,求当 ≤x≤2时,函数y的取值范围.
C
自主拓展——综合
进一步尝试:
在函数y=- , y=-x+5, y=2x的图象中,是中心对称图形且对称中心是原点的是____
动动脑筋:
在一个反比例函数图象上任取两点P、Q,过P、 Q两点分别作x轴、y轴的平行线(或垂线),与坐 标轴围成的矩形面积为S1和S2,那么S1与S2有什么 大小关系?
x
2
我学会了_______________
我认识到_______________
我有困惑_______________
课后思考:
(1)为什么反比例函数图象与x轴
(2)在一个反比例函数图象上任取点P,过P点分别作x轴、y轴的平行线(或垂线),与坐 标轴围成的矩形面积为S,与k有什么关系?
y轴无限接近却永不相交?
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
