第十八章 平行四边形章末复习:微专题 3矩形的综合训练(含答案)
文档属性
| 名称 | 第十八章 平行四边形章末复习:微专题 3矩形的综合训练(含答案) | 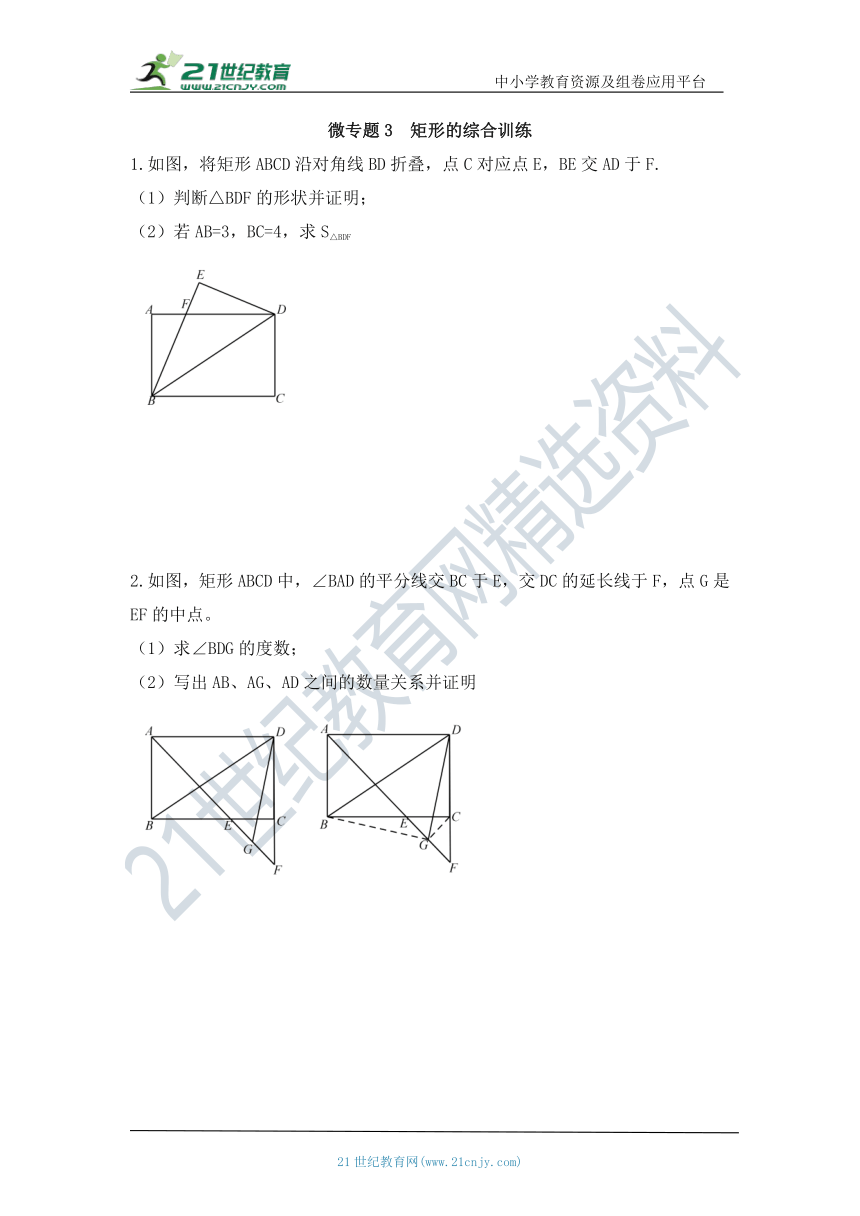 | |
| 格式 | docx | ||
| 文件大小 | 130.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 20:32:17 | ||
图片预览




文档简介
微专题3 矩形的综合训练
1.如图,将矩形ABCD沿对角线BD折叠,点C对应点E,BE交AD于F.
(1)判断△BDF的形状并证明;
(2)若AB=3,BC=4,求S△BDF
2.如图,矩形ABCD中,∠BAD的平分线交BC于E,交DC的延长线于F,点G是EF的中点。
(1)求∠BDG的度数;
(2)写出AB、AG、AD之间的数量关系并证明
3.如图,矩形ABCD中,E在BC上,CG⊥BD于G,交AE的延长线于F,CF=BD,求∠BAF。
4.如图,矩形ABCD中,E为BC中点,M为DA延长线上一点,MB、DE的延长线交于N,且∠MNC=90°。(1)求证:AD=2NE;(2)求证:DM=DN.
5.如图,点E是□ABCD中边BC的中点,连接AE并延长,交DC的延长线于点F.
(1) 求证:△ABE ≌△FCE
(2)连接AC、BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.
6.如图,在 ABC中,BD⊥AC于D,CE⊥AB于E,点M,N分别是BC,DE的中点
(1) 求证:MN⊥DE
(2)连接ME,MD,若∠A=60°,求false解的值.
7.如图,矩形ABCD中,E为CD中点,BF平分∠ABC,BE⊥EF
(1) ∠AED的度数
(2)求证:GF=2DF.
8.(1)如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,小明将G延长交DC于点F,认为GF=DF,你同意吗?请说明理由.
(2)保持(1)中的条件不变,若DC=2DF,求false 的值;
(3)保持(1)中的条件不变,若DC=nDF,直接写出false 的值为 .
微专题3 矩形的综合训练
1.如图,将矩形ABCD沿对角线BD折叠,点C对应点E,BE交AD于F.
(1)判断△BDF的形状并证明;
(2)若AB=3,BC=4,求S△BDF
(1)证明:∵ AD∥BC ∴ ∠DBC=∠ADB
又 ∵ ∠DBC=∠EBD ∴ ∠EBD=∠ADB
∴ △BDF为等腰三角形
(2)解:由(1)知BF=FD,设AF=x ∴FD=BF=4-x
∴ 9+x2=(4-x)2 ∴ x=false ∴ DF=false
∴ S△ADF=falseDF·AB=false×false×3=false
2.如图,矩形ABCD中,∠BAD的平分线交BC于E,交DC的延长线于F,点G是EF的中点。
(1)求∠BDG的度数;
(2)写出AB、AG、AD之间的数量关系并证明
(1)解:连接CG、BG,△DGF≌△BGC
∴ DG=BG,∠DGB=∠CGF=90°
∴ △DGB为等腰直角三角形 ∴∠BDG=45°
(2)证明:AG=AE+EG=falseAB+EG,AD=BC=BE+EC=AB+falseEG
∴ AB+BC=falseAG
3.如图,矩形ABCD中,E在BC上,CG⊥BD于G,交AE的延长线于F,CF=BD,求∠BAF。
解:连接AC,延长DC交EF于点M,可证△CMF≌△CEA(ASA)
∴ EC=MC
∴ ∠CEM=∠AEB=45°
∴ ∠BAF=45°
4.如图,矩形ABCD中,E为BC中点,M为DA延长线上一点,MB、DE的延长线交于N,且∠MNC=90°。(1)求证:AD=2NE;(2)求证:DM=DN.
证明:(1)∵E为BC中点,∠CNB=90° ∴NE=CE=BE=falseBC=falseAD
∴ AD=2NE
(2)∵AD∥BC,∴∠M=∠CBN
又∵EB=EN ∴ ∠CBN=∠ENB
∴ ∠ENB=∠M ∴ DM=DN
5.如图,点E是□ABCD中边BC的中点,连接AE并延长,交DC的延长线于点F.
(1) 求证:△ABE ≌△FCE
(2)连接AC、BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.
答案:
证明:(1)∵∠AEB=∠CEF,∠ECF=∠EBA,BE=CE. ∴△ABE ≌△FCE
(2)∵∠AEC=2∠ABC=∠ABC +∠BAE ∴∠ABC=∠BAE,∴AE=BE=CE.
∴∠BAC=90°又∵AB ∥CF且AB =CF ∴四边形ABFC为矩形
6.如图,在 ABC中,BD⊥AC于D,CE⊥AB于E,点M,N分别是BC,DE的中点
(1) 求证:MN⊥DE
(2)连接ME,MD,若∠A=60°,求false解的值.
答案:
(1)证明,连接ME, MD,可证ME=MD=falseBC
∵N为ED的中点,∴MN⊥DE
∠ABC+∠ACB=120°∴∠BME+∠CMD=120° ∴∠DME=60°
false∴△EMD为等边三角形,
∴
7.如图,矩形ABCD中,E为CD中点,BF平分∠ABC,BE⊥EF
(1) ∠AED的度数
(2)求证:GF=2DF.
答案:
解(1)作AQ⊥EF,AH⊥BE,∵∠BAF=∠FEB=90° ∴∠AFQ=∠ABH
∴△AFQ ≌△ABH ∴AH=AQ,∴∠BAF=∠FEB= false∠BEF=45°
(2)证明:作EN⊥BF,由(1)知∠AEB=∠AFB=45°∴∠DAE=∠NBE
可证△DEA≌△NEB ∴DF=NF
可证N为FG中点,∴GP=2DF
8.(1)如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,小明将G延长交DC于点F,认为GF=DF,你同意吗?请说明理由.
(2)保持(1)中的条件不变,若DC=2DF,求false 的值;
(3)保持(1)中的条件不变,若DC=nDF,直接写出false 的值为 .
答案:
解:(1)相等,连接EF, ∵DE=AE=EG,∴△DEF≌ △GEF, ∴GF=DF
(2)设DF=1,则CD=2,CF=1,GF=DF=1, BG=AB=2,AE=DE= x,BC=AD=2x
在Rt△BCF中(2+1)2=12+(2x)2, x= false ,false.
(3)设DF=1,CD=n,AE=DE=x.则(n+1)2=(n-1)2+(2x)2 x=false,false
1.如图,将矩形ABCD沿对角线BD折叠,点C对应点E,BE交AD于F.
(1)判断△BDF的形状并证明;
(2)若AB=3,BC=4,求S△BDF
2.如图,矩形ABCD中,∠BAD的平分线交BC于E,交DC的延长线于F,点G是EF的中点。
(1)求∠BDG的度数;
(2)写出AB、AG、AD之间的数量关系并证明
3.如图,矩形ABCD中,E在BC上,CG⊥BD于G,交AE的延长线于F,CF=BD,求∠BAF。
4.如图,矩形ABCD中,E为BC中点,M为DA延长线上一点,MB、DE的延长线交于N,且∠MNC=90°。(1)求证:AD=2NE;(2)求证:DM=DN.
5.如图,点E是□ABCD中边BC的中点,连接AE并延长,交DC的延长线于点F.
(1) 求证:△ABE ≌△FCE
(2)连接AC、BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.
6.如图,在 ABC中,BD⊥AC于D,CE⊥AB于E,点M,N分别是BC,DE的中点
(1) 求证:MN⊥DE
(2)连接ME,MD,若∠A=60°,求false解的值.
7.如图,矩形ABCD中,E为CD中点,BF平分∠ABC,BE⊥EF
(1) ∠AED的度数
(2)求证:GF=2DF.
8.(1)如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,小明将G延长交DC于点F,认为GF=DF,你同意吗?请说明理由.
(2)保持(1)中的条件不变,若DC=2DF,求false 的值;
(3)保持(1)中的条件不变,若DC=nDF,直接写出false 的值为 .
微专题3 矩形的综合训练
1.如图,将矩形ABCD沿对角线BD折叠,点C对应点E,BE交AD于F.
(1)判断△BDF的形状并证明;
(2)若AB=3,BC=4,求S△BDF
(1)证明:∵ AD∥BC ∴ ∠DBC=∠ADB
又 ∵ ∠DBC=∠EBD ∴ ∠EBD=∠ADB
∴ △BDF为等腰三角形
(2)解:由(1)知BF=FD,设AF=x ∴FD=BF=4-x
∴ 9+x2=(4-x)2 ∴ x=false ∴ DF=false
∴ S△ADF=falseDF·AB=false×false×3=false
2.如图,矩形ABCD中,∠BAD的平分线交BC于E,交DC的延长线于F,点G是EF的中点。
(1)求∠BDG的度数;
(2)写出AB、AG、AD之间的数量关系并证明
(1)解:连接CG、BG,△DGF≌△BGC
∴ DG=BG,∠DGB=∠CGF=90°
∴ △DGB为等腰直角三角形 ∴∠BDG=45°
(2)证明:AG=AE+EG=falseAB+EG,AD=BC=BE+EC=AB+falseEG
∴ AB+BC=falseAG
3.如图,矩形ABCD中,E在BC上,CG⊥BD于G,交AE的延长线于F,CF=BD,求∠BAF。
解:连接AC,延长DC交EF于点M,可证△CMF≌△CEA(ASA)
∴ EC=MC
∴ ∠CEM=∠AEB=45°
∴ ∠BAF=45°
4.如图,矩形ABCD中,E为BC中点,M为DA延长线上一点,MB、DE的延长线交于N,且∠MNC=90°。(1)求证:AD=2NE;(2)求证:DM=DN.
证明:(1)∵E为BC中点,∠CNB=90° ∴NE=CE=BE=falseBC=falseAD
∴ AD=2NE
(2)∵AD∥BC,∴∠M=∠CBN
又∵EB=EN ∴ ∠CBN=∠ENB
∴ ∠ENB=∠M ∴ DM=DN
5.如图,点E是□ABCD中边BC的中点,连接AE并延长,交DC的延长线于点F.
(1) 求证:△ABE ≌△FCE
(2)连接AC、BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.
答案:
证明:(1)∵∠AEB=∠CEF,∠ECF=∠EBA,BE=CE. ∴△ABE ≌△FCE
(2)∵∠AEC=2∠ABC=∠ABC +∠BAE ∴∠ABC=∠BAE,∴AE=BE=CE.
∴∠BAC=90°又∵AB ∥CF且AB =CF ∴四边形ABFC为矩形
6.如图,在 ABC中,BD⊥AC于D,CE⊥AB于E,点M,N分别是BC,DE的中点
(1) 求证:MN⊥DE
(2)连接ME,MD,若∠A=60°,求false解的值.
答案:
(1)证明,连接ME, MD,可证ME=MD=falseBC
∵N为ED的中点,∴MN⊥DE
∠ABC+∠ACB=120°∴∠BME+∠CMD=120° ∴∠DME=60°
false∴△EMD为等边三角形,
∴
7.如图,矩形ABCD中,E为CD中点,BF平分∠ABC,BE⊥EF
(1) ∠AED的度数
(2)求证:GF=2DF.
答案:
解(1)作AQ⊥EF,AH⊥BE,∵∠BAF=∠FEB=90° ∴∠AFQ=∠ABH
∴△AFQ ≌△ABH ∴AH=AQ,∴∠BAF=∠FEB= false∠BEF=45°
(2)证明:作EN⊥BF,由(1)知∠AEB=∠AFB=45°∴∠DAE=∠NBE
可证△DEA≌△NEB ∴DF=NF
可证N为FG中点,∴GP=2DF
8.(1)如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,小明将G延长交DC于点F,认为GF=DF,你同意吗?请说明理由.
(2)保持(1)中的条件不变,若DC=2DF,求false 的值;
(3)保持(1)中的条件不变,若DC=nDF,直接写出false 的值为 .
答案:
解:(1)相等,连接EF, ∵DE=AE=EG,∴△DEF≌ △GEF, ∴GF=DF
(2)设DF=1,则CD=2,CF=1,GF=DF=1, BG=AB=2,AE=DE= x,BC=AD=2x
在Rt△BCF中(2+1)2=12+(2x)2, x= false ,false.
(3)设DF=1,CD=n,AE=DE=x.则(n+1)2=(n-1)2+(2x)2 x=false,false
