4.1.2 函数的表示法同步练习(含解析)
文档属性
| 名称 | 4.1.2 函数的表示法同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 00:00:00 | ||
图片预览




文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册4.1.2函数的表示方法
同步练习
一、单选题(共10题;共20分)
1.下面关于函数的三种表示方法叙述错误的是(???
)
A.?用图象法表示函数关系,可以直观地看出函数值如何随着自变量而变化
B.?用列表法表示函数关系,可以很清楚地看出自变量取的值与对应的函数值
C.?用公式法表示函数关系,可以方便地计算函数值
D.?任何函数关系都可以用上述三种方法来表示
2.在某次试验中,测得两个变量
和
之间的4组对应数据如下表:
1
2
3
4
0
3
8
15
则
与
之间的关系满足下列关系式(??
)
A.?
?????????????????????????B.??????????????????????????C.??????????????????????????D.?
3.2013年8月16日,广东省遭受台风“尤特”袭击,大部分地区发生强降雨,某河受暴雨袭击,一天的水位记录如表,观察表中数据,水位上升最快的时段是( )
A.?8~12时??????????????????????????B.?12~16时??????????????????????????C.?16~20时??????????????????????????D.?20~24时
4.下列关系式:①x2-3x=4;②S=3.5t;③y=
;④y=5x-3;⑤C=2πR;⑥S=v0t+
at2;⑦2y+y2=0,其中不是函数关系的是(???
)
A.?①⑦?????????????????????????????????B.?①②③④?????????????????????????????????C.?④⑥?????????????????????????????????D.?①②⑦
5.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表,由上表可知下列说法错误的是( )
A.?弹簧的长度随物体质量的变化而变化,其中物体的质量是自变量,弹簧的长度是因变量
B.?如果物体的质量为4kg,那么弹簧的长度为14cm
C.?在弹簧能承受的范围内,当物体的质量为6kg时,弹簧的长度为16cm
D.?在没挂物体时,弹簧的长度为12cm
6.某超市某种商品的单价为70元/件,若买x件该商品的总价为y元,则其中的常量是( )
A.?70????????????????????????????????????????B.?x????????????????????????????????????????C.?y????????????????????????????????????????D.?不确定
7.下列各表达式不是表示y与x的函数的是( )
A.?y=3x2???????????????????????????B.?y=???????????????????????????C.?y=±(x>0)???????????????????????????D.?y=3x+1
8.已知函数y=ax﹣3(a是常量,且a≠0),当x=1时,y=7,则a的值为( )
A.?4?????????????????????????????????????????B.?-4?????????????????????????????????????????C.?10?????????????????????????????????????????D.?-10
9.函数y=中自变量的取值范围是( )
A.?x≠0????????????????????????????????????B.?x≠2????????????????????????????????????C.?x≠﹣2????????????????????????????????????D.?x=2
10.已知矩形的面积为36cm2
,
相邻两条边长分别为xcm和ycm,则y与x之间的函数图象正确的是(??
)
A.????????????????B.????????????????C.????????????????D.?
二、填空题(共5题;共16分)
11.表示两个变量之间的关系常用的三种方法是________、________和________.
12.下表所列为某商店薄利多销的情况.某商品原价为560元,随着不同幅度的降价,日销量(单位为件)发生相应的变化(如表):
降价(元)
5
10
15
20
25
30
35
日销量(件)
780
810
840
870
900
930
960
这个表反映了________个变量之间的关系,________是自变量,________是因变量.从表中可以看出每降价5元,日销量增加________件,从而可以估计降价之前的日销量为________件,如果售价为500元时,日销量为________件.
13.据国家统计局统计,新中国成立以来至2000年,我国各项税收收入合计见表.
年份
1950
1955
1960
1965
1970
1975
1980
1985
1990
1995
2000
税收收入/亿
48.98
127.45
203.65
204.30
281.20
402.77
571.70
2040.79
2821.86
6038.04
12581.51
从表中可以得出:新中国成立以来我国的税收收人总体趋势是________,其中,________年与5年前相比,增长百分数最大;________年与5年前相比,增长百分数最小;2000年与1950年相比,税收收入增长了________倍(保留一位小数).
14.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下从表中可知音速y随温度x的升高而________?在气温为20℃的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令地点________?米.
气温(x/℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
15.某市的出租车收费按里程计算,3km内(含3km)收费5元,超过3km,每增加1km加收1元,则路程x≥3时,车费y(元)与x(km)之间的关系式是________.
三、解答题(共2题;共10分)
16.在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
(3)若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
17.某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
四、综合题(共3题;共55分)
18.日常生活中,我们经常要煮开水,下表为煮开水的时间与水的温度的描述.
?时间(分)
?1
?2
?3
4
?5
?6
?7
?8
?9
?10
?11
?12
?13
?温度
(℃)
?25
?29
?32
?43
?52
?61
?72
?81
?90
?98
?100
?100
?100
(1)根据上表的数据,我们得到什么信息?
(2)在第9分钟时,水可以喝吗?为什么?在11分钟时呢?
(3)根据表格的数据判断:在第15分钟时,水的温度为多少高呢?
(4)随着加热时间的增长,水的温度是否会一直上升?说明你判断的依据.
19.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
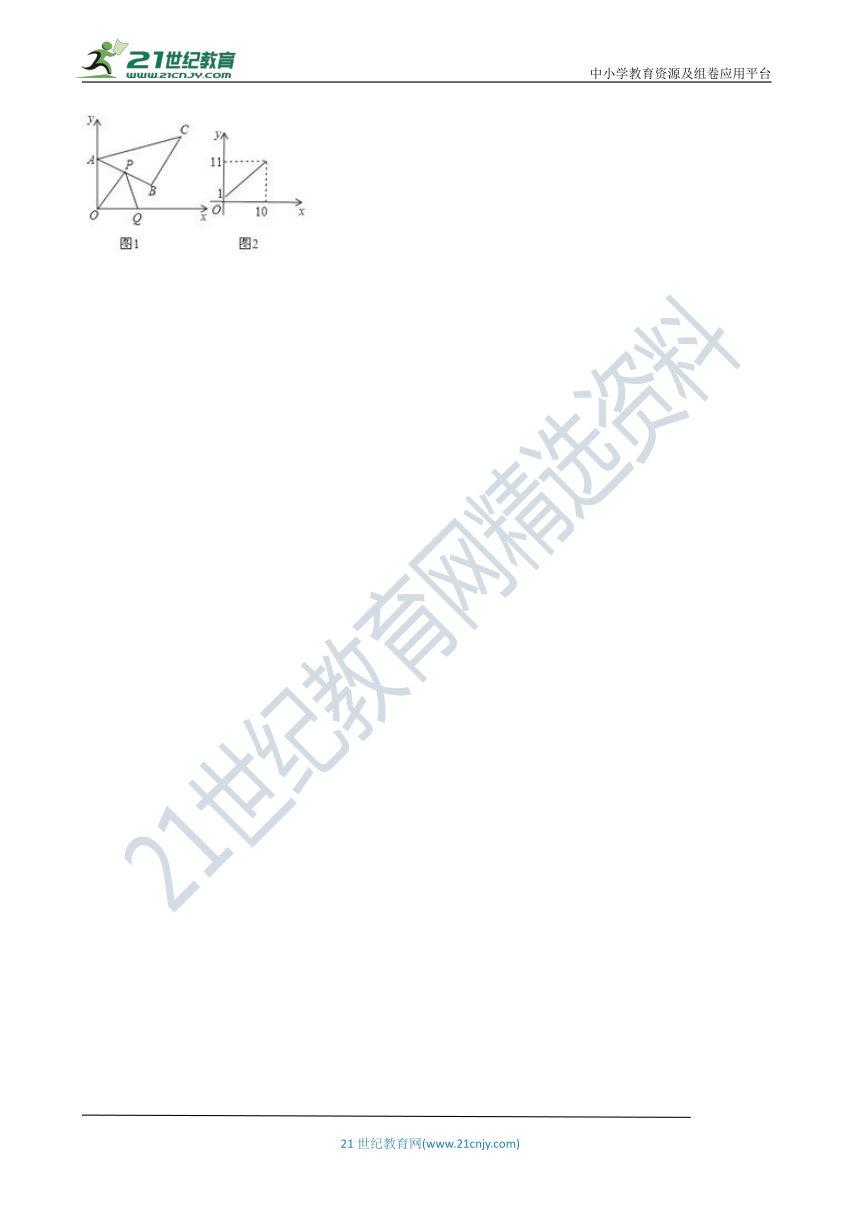
20.如图1,将等腰直角△ABC放在直角坐标系中,其中∠B=90°,A(0,10),B(8,4),动点P在直角边上,沿着A﹣B﹣C匀速运动,同时点Q在x轴正半轴上以同样的速度运动,当点P到达C时,两点同时停止运动.设运动时间为t秒,当点P在AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图2所示,
(1)则Q开始运动时的坐标是?P点运动的速度是?
(2)求AB的长及点C的坐标;
(3)问当t为何值时,OP=PQ?
答案解析部分
一、单选题
1.【答案】
D
解:A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化,正确;
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值,正确;
C.用公式法表示函数关系,可以方便地计算函数值,正确;
D.并不是任何函数关系都可以用上述三种方法来表示,错误.
故答案为:D.
2.【答案】
C
解:将x=1代入
得,y=0,将x=2代入
得y=2,与表格中的3不相等,故A选项不符合题意;
将x=1代入
得,y=0,将x=2代入
得y=3,将x=3代入
得y=6,与表格中8不相等,故B选项不符合题意;
将x=1代入
得y=0,将剩下的几个值代入得出的y都与表格相等,故C符合题意;
同理D选项不符合题意.
故答案为:C.
3.【答案】
D
解:由表可以看出:在相等的时间间隔内,20时至24时水位上升最快.
故选D.
4.【答案】
A
解:函数是指两个变量之间的关系,而①⑦只有一个变量,故①⑦不是函数;②③④⑤都有两个变量,并且给等号右边的变量一个确定的值,等号左边的变量都只有唯一的值与之对应,所以②③④⑤都是函数;⑥是以后将要学习的一个物理公式,对于一个确定的运动过程而言,v0和a都是不变的,只有S和t两个变量,并且满足一一对应,故⑥也是函数。
5.【答案】
C
解:A、弹簧的长度随物体质量的变化而变化,其中物体的质量是自变量,弹簧的长度是因变量,正确,故本选项错误;
B、如果物体的质量为4kg,那么弹簧的长度为14cm,正确,故本选项错误;
C、应为在弹簧能承受的范围内,当物体的质量为6kg时,弹簧的长度为15cm,故本选项正确;
D、在没挂物体时,弹簧的长度为12cm,正确,故本选项错误.
故选C.
6.【答案】
A
解:根据题意得,y=70x,
∴常量是70.
故选A.
7.【答案】
C
解:A、y=3x2对于x的每一个取值,y都有唯一确定的值,符合函数的定义,故本选项正确;
B、y=对于x的每一个取值,y都有唯一确定的值,符合函数的定义,故本选项正确;
C、y=±(x>0)对于x的每一个取值,y有两个值,不符合函数的定义,故本选项错误;
D、y=3x+1对于x的每一个取值,y都有唯一确定的值,符合函数的定义,故本选项正确.
故选C.
8.【答案】
C
解:根据题意得:a×1﹣3=7,
解得:a=10.
故选C.
9.【答案】
B
解:根据题意得:x﹣2≠0,解得x≠2.
故选B.
10.【答案】
A
解:因为x和y为矩形的两条边
∴x>0,y>0
故答案为:A.
二、填空题
11.【答案】
表格法;关系式法;图象法
解:表示两个变量之间的关系常用的三种方法是表格法、关系式法和图象法,
故答案为:表格法,关系式法,图象法.
12.【答案】两;降价(元);日销量;30;750;1110
解:∵日销量随降价的改变而改变,
∴降价(元)是自变量,日销量是因变量.
从表中可:日销量与降价之间的关系为:
日销量=750+(原价﹣售价)÷5×30;
则可以估计降价之前的日销量为780﹣30=750件,
售价为500元时,日销量=750+(560﹣500)÷5×30=1110件.
13.【答案】上升;1985;1965;255.9
解:(127.45﹣48.98)÷48.98≈160.2%;
(203.65﹣127.45)÷127.45≈59.8%;
(204.30﹣203.65)÷203.65≈0.3%;
(281.20﹣204.30)÷204.30≈37.6%;
(402.77﹣281.20)÷281.20≈43.2%;
(571.70﹣402.77)÷402.77≈41.9%;
(2040.79﹣571.70)÷571.70≈257.0%;
(2821.86﹣2040.79)÷2040.79≈38.3%;
(6038.04﹣2821.86)÷2821.86≈114.0%;
(12581.51﹣6038.04)÷6038.04≈108.4%;
(12581.51﹣48.98)÷48.98≈255.9(倍);
新中国成立以来我国的税收收人总体趋势是上升,其中,1985年与5年前相比,增长百分数最大;1965年与5年前相比,增长百分数最小;2000年与1950年相比,税收收入增长了25587.0倍.
故答案为:上升;1985;1965;255.9.
14.【答案】加快;68.6
解:观察表中的数据可知,音速随温度的升高而加快;
当气温为20℃时,音速为343米/秒,而该人是看到发令枪的烟0.2秒后,听到了枪声.
则由此可知,这个人距发令地点343×0.2=68.6米.
15.【答案】y=x+2
【考点】函数关系式
【解析】【解答】解:由题意得:y=5+(x﹣3)×1=x+2.
故答案为:y=x+2.
三、解答题
16.【答案】
解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
(2)当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;
(3)根据上表可知所挂重物为7千克时(在允许范围内)时的弹簧长度=18+2×7=32厘米.
17.【答案】
解:(1)依题意得:学校离王老师家有10千米,从出发到学校王老师用了25分钟;
(2)依题意得:王老师吃早餐用了10分钟;
(3)吃早餐以前的速度为:5÷10=0.5km/分钟,吃完早餐以后的速度为:(10﹣5)÷(25﹣20)=1km/分钟=60km/小时,
∴王老师吃完早餐以后速度快,最快时速达到60km/小时.
综合题
18.【答案】
(1)解:随着时间的加长,水的温度在逐渐升高,11分钟时达到开水温度
(2)解:在第9分钟时,水不可以喝,因为水还没有烧开,在11分钟时,水烧开,可以喝
(3)解:第15分钟时,水的温度为100℃
(4)解:随着加热时间的增长,水的温度不会一直上升,因为水温升高到100℃时,水温不再升高
19.【答案】
(1)解答:由函数图象,得图象表示了时间、距离的关系,自变量是时间,因变量是距离;
(2)解答:由纵坐标看出10时他距家15千米,13时他距家30千米;
(3)解答:由横坐标看出12:00时离家最远,由纵坐标看出离家30千米;
(4)解答:由纵坐标看出11时距家19千米,12时距家30千米,11时到12时他行驶了30-19=11(千米);
答:11时到12时他行驶了11千米.
(5)解答:由纵坐标看出12:00-13:00时距离没变且时间较长,得12:00-13:00休息并吃午饭;
(6)解答:由横坐标看出回家时用了2两小时,由纵坐标看出路程是30千米,回家的速度是30÷2=15(千米/小时)
答:他由离家最远的地方返回时的平均速度是15千米/小时。
20.【答案】
解:(1)根据题意,易得Q(1,0),
点P运动速度每秒钟1个单位长度.
故答案为:(1,0);每秒钟1个单位长度.
(2)过点B作BF⊥y轴于点F,BE⊥x轴于点E,则BF=8,OF=BE=4.
∴AF=10﹣4=6.
在Rt△AFB中,
过点C作CG⊥x轴于点G,与FB的延长线交于点H.
∵∠ABC=90°=∠AFB=∠BHC
∴∠ABF+∠CBH=90°,∠ABF=∠BCH,∠FAB=∠CBH,
∴△ABF≌△BCH.
∴BH=AF=6,CH=BF=8.
∴AB==10,
∴OG=FH=8+6=14,CG=8+4=12.
∴所求C点的坐标为(14,12);
(3)当点P在AB上时,若OP=PQ,则ON=NQ,
∵△APM∽△ABF,AP=t,AB=10,BF=8,
∴ON=PM=t,
又∵ON=OQ=(t+1),
∴t=(t+1),
解得:t=
,
当点P在BC上时,t的值不存在.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册4.1.2函数的表示方法
同步练习
一、单选题(共10题;共20分)
1.下面关于函数的三种表示方法叙述错误的是(???
)
A.?用图象法表示函数关系,可以直观地看出函数值如何随着自变量而变化
B.?用列表法表示函数关系,可以很清楚地看出自变量取的值与对应的函数值
C.?用公式法表示函数关系,可以方便地计算函数值
D.?任何函数关系都可以用上述三种方法来表示
2.在某次试验中,测得两个变量
和
之间的4组对应数据如下表:
1
2
3
4
0
3
8
15
则
与
之间的关系满足下列关系式(??
)
A.?
?????????????????????????B.??????????????????????????C.??????????????????????????D.?
3.2013年8月16日,广东省遭受台风“尤特”袭击,大部分地区发生强降雨,某河受暴雨袭击,一天的水位记录如表,观察表中数据,水位上升最快的时段是( )
A.?8~12时??????????????????????????B.?12~16时??????????????????????????C.?16~20时??????????????????????????D.?20~24时
4.下列关系式:①x2-3x=4;②S=3.5t;③y=
;④y=5x-3;⑤C=2πR;⑥S=v0t+
at2;⑦2y+y2=0,其中不是函数关系的是(???
)
A.?①⑦?????????????????????????????????B.?①②③④?????????????????????????????????C.?④⑥?????????????????????????????????D.?①②⑦
5.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表,由上表可知下列说法错误的是( )
A.?弹簧的长度随物体质量的变化而变化,其中物体的质量是自变量,弹簧的长度是因变量
B.?如果物体的质量为4kg,那么弹簧的长度为14cm
C.?在弹簧能承受的范围内,当物体的质量为6kg时,弹簧的长度为16cm
D.?在没挂物体时,弹簧的长度为12cm
6.某超市某种商品的单价为70元/件,若买x件该商品的总价为y元,则其中的常量是( )
A.?70????????????????????????????????????????B.?x????????????????????????????????????????C.?y????????????????????????????????????????D.?不确定
7.下列各表达式不是表示y与x的函数的是( )
A.?y=3x2???????????????????????????B.?y=???????????????????????????C.?y=±(x>0)???????????????????????????D.?y=3x+1
8.已知函数y=ax﹣3(a是常量,且a≠0),当x=1时,y=7,则a的值为( )
A.?4?????????????????????????????????????????B.?-4?????????????????????????????????????????C.?10?????????????????????????????????????????D.?-10
9.函数y=中自变量的取值范围是( )
A.?x≠0????????????????????????????????????B.?x≠2????????????????????????????????????C.?x≠﹣2????????????????????????????????????D.?x=2
10.已知矩形的面积为36cm2
,
相邻两条边长分别为xcm和ycm,则y与x之间的函数图象正确的是(??
)
A.????????????????B.????????????????C.????????????????D.?
二、填空题(共5题;共16分)
11.表示两个变量之间的关系常用的三种方法是________、________和________.
12.下表所列为某商店薄利多销的情况.某商品原价为560元,随着不同幅度的降价,日销量(单位为件)发生相应的变化(如表):
降价(元)
5
10
15
20
25
30
35
日销量(件)
780
810
840
870
900
930
960
这个表反映了________个变量之间的关系,________是自变量,________是因变量.从表中可以看出每降价5元,日销量增加________件,从而可以估计降价之前的日销量为________件,如果售价为500元时,日销量为________件.
13.据国家统计局统计,新中国成立以来至2000年,我国各项税收收入合计见表.
年份
1950
1955
1960
1965
1970
1975
1980
1985
1990
1995
2000
税收收入/亿
48.98
127.45
203.65
204.30
281.20
402.77
571.70
2040.79
2821.86
6038.04
12581.51
从表中可以得出:新中国成立以来我国的税收收人总体趋势是________,其中,________年与5年前相比,增长百分数最大;________年与5年前相比,增长百分数最小;2000年与1950年相比,税收收入增长了________倍(保留一位小数).
14.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下从表中可知音速y随温度x的升高而________?在气温为20℃的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令地点________?米.
气温(x/℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
15.某市的出租车收费按里程计算,3km内(含3km)收费5元,超过3km,每增加1km加收1元,则路程x≥3时,车费y(元)与x(km)之间的关系式是________.
三、解答题(共2题;共10分)
16.在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
(3)若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
17.某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
四、综合题(共3题;共55分)
18.日常生活中,我们经常要煮开水,下表为煮开水的时间与水的温度的描述.
?时间(分)
?1
?2
?3
4
?5
?6
?7
?8
?9
?10
?11
?12
?13
?温度
(℃)
?25
?29
?32
?43
?52
?61
?72
?81
?90
?98
?100
?100
?100
(1)根据上表的数据,我们得到什么信息?
(2)在第9分钟时,水可以喝吗?为什么?在11分钟时呢?
(3)根据表格的数据判断:在第15分钟时,水的温度为多少高呢?
(4)随着加热时间的增长,水的温度是否会一直上升?说明你判断的依据.
19.小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
20.如图1,将等腰直角△ABC放在直角坐标系中,其中∠B=90°,A(0,10),B(8,4),动点P在直角边上,沿着A﹣B﹣C匀速运动,同时点Q在x轴正半轴上以同样的速度运动,当点P到达C时,两点同时停止运动.设运动时间为t秒,当点P在AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图2所示,
(1)则Q开始运动时的坐标是?P点运动的速度是?
(2)求AB的长及点C的坐标;
(3)问当t为何值时,OP=PQ?
答案解析部分
一、单选题
1.【答案】
D
解:A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化,正确;
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值,正确;
C.用公式法表示函数关系,可以方便地计算函数值,正确;
D.并不是任何函数关系都可以用上述三种方法来表示,错误.
故答案为:D.
2.【答案】
C
解:将x=1代入
得,y=0,将x=2代入
得y=2,与表格中的3不相等,故A选项不符合题意;
将x=1代入
得,y=0,将x=2代入
得y=3,将x=3代入
得y=6,与表格中8不相等,故B选项不符合题意;
将x=1代入
得y=0,将剩下的几个值代入得出的y都与表格相等,故C符合题意;
同理D选项不符合题意.
故答案为:C.
3.【答案】
D
解:由表可以看出:在相等的时间间隔内,20时至24时水位上升最快.
故选D.
4.【答案】
A
解:函数是指两个变量之间的关系,而①⑦只有一个变量,故①⑦不是函数;②③④⑤都有两个变量,并且给等号右边的变量一个确定的值,等号左边的变量都只有唯一的值与之对应,所以②③④⑤都是函数;⑥是以后将要学习的一个物理公式,对于一个确定的运动过程而言,v0和a都是不变的,只有S和t两个变量,并且满足一一对应,故⑥也是函数。
5.【答案】
C
解:A、弹簧的长度随物体质量的变化而变化,其中物体的质量是自变量,弹簧的长度是因变量,正确,故本选项错误;
B、如果物体的质量为4kg,那么弹簧的长度为14cm,正确,故本选项错误;
C、应为在弹簧能承受的范围内,当物体的质量为6kg时,弹簧的长度为15cm,故本选项正确;
D、在没挂物体时,弹簧的长度为12cm,正确,故本选项错误.
故选C.
6.【答案】
A
解:根据题意得,y=70x,
∴常量是70.
故选A.
7.【答案】
C
解:A、y=3x2对于x的每一个取值,y都有唯一确定的值,符合函数的定义,故本选项正确;
B、y=对于x的每一个取值,y都有唯一确定的值,符合函数的定义,故本选项正确;
C、y=±(x>0)对于x的每一个取值,y有两个值,不符合函数的定义,故本选项错误;
D、y=3x+1对于x的每一个取值,y都有唯一确定的值,符合函数的定义,故本选项正确.
故选C.
8.【答案】
C
解:根据题意得:a×1﹣3=7,
解得:a=10.
故选C.
9.【答案】
B
解:根据题意得:x﹣2≠0,解得x≠2.
故选B.
10.【答案】
A
解:因为x和y为矩形的两条边
∴x>0,y>0
故答案为:A.
二、填空题
11.【答案】
表格法;关系式法;图象法
解:表示两个变量之间的关系常用的三种方法是表格法、关系式法和图象法,
故答案为:表格法,关系式法,图象法.
12.【答案】两;降价(元);日销量;30;750;1110
解:∵日销量随降价的改变而改变,
∴降价(元)是自变量,日销量是因变量.
从表中可:日销量与降价之间的关系为:
日销量=750+(原价﹣售价)÷5×30;
则可以估计降价之前的日销量为780﹣30=750件,
售价为500元时,日销量=750+(560﹣500)÷5×30=1110件.
13.【答案】上升;1985;1965;255.9
解:(127.45﹣48.98)÷48.98≈160.2%;
(203.65﹣127.45)÷127.45≈59.8%;
(204.30﹣203.65)÷203.65≈0.3%;
(281.20﹣204.30)÷204.30≈37.6%;
(402.77﹣281.20)÷281.20≈43.2%;
(571.70﹣402.77)÷402.77≈41.9%;
(2040.79﹣571.70)÷571.70≈257.0%;
(2821.86﹣2040.79)÷2040.79≈38.3%;
(6038.04﹣2821.86)÷2821.86≈114.0%;
(12581.51﹣6038.04)÷6038.04≈108.4%;
(12581.51﹣48.98)÷48.98≈255.9(倍);
新中国成立以来我国的税收收人总体趋势是上升,其中,1985年与5年前相比,增长百分数最大;1965年与5年前相比,增长百分数最小;2000年与1950年相比,税收收入增长了25587.0倍.
故答案为:上升;1985;1965;255.9.
14.【答案】加快;68.6
解:观察表中的数据可知,音速随温度的升高而加快;
当气温为20℃时,音速为343米/秒,而该人是看到发令枪的烟0.2秒后,听到了枪声.
则由此可知,这个人距发令地点343×0.2=68.6米.
15.【答案】y=x+2
【考点】函数关系式
【解析】【解答】解:由题意得:y=5+(x﹣3)×1=x+2.
故答案为:y=x+2.
三、解答题
16.【答案】
解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
(2)当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;
(3)根据上表可知所挂重物为7千克时(在允许范围内)时的弹簧长度=18+2×7=32厘米.
17.【答案】
解:(1)依题意得:学校离王老师家有10千米,从出发到学校王老师用了25分钟;
(2)依题意得:王老师吃早餐用了10分钟;
(3)吃早餐以前的速度为:5÷10=0.5km/分钟,吃完早餐以后的速度为:(10﹣5)÷(25﹣20)=1km/分钟=60km/小时,
∴王老师吃完早餐以后速度快,最快时速达到60km/小时.
综合题
18.【答案】
(1)解:随着时间的加长,水的温度在逐渐升高,11分钟时达到开水温度
(2)解:在第9分钟时,水不可以喝,因为水还没有烧开,在11分钟时,水烧开,可以喝
(3)解:第15分钟时,水的温度为100℃
(4)解:随着加热时间的增长,水的温度不会一直上升,因为水温升高到100℃时,水温不再升高
19.【答案】
(1)解答:由函数图象,得图象表示了时间、距离的关系,自变量是时间,因变量是距离;
(2)解答:由纵坐标看出10时他距家15千米,13时他距家30千米;
(3)解答:由横坐标看出12:00时离家最远,由纵坐标看出离家30千米;
(4)解答:由纵坐标看出11时距家19千米,12时距家30千米,11时到12时他行驶了30-19=11(千米);
答:11时到12时他行驶了11千米.
(5)解答:由纵坐标看出12:00-13:00时距离没变且时间较长,得12:00-13:00休息并吃午饭;
(6)解答:由横坐标看出回家时用了2两小时,由纵坐标看出路程是30千米,回家的速度是30÷2=15(千米/小时)
答:他由离家最远的地方返回时的平均速度是15千米/小时。
20.【答案】
解:(1)根据题意,易得Q(1,0),
点P运动速度每秒钟1个单位长度.
故答案为:(1,0);每秒钟1个单位长度.
(2)过点B作BF⊥y轴于点F,BE⊥x轴于点E,则BF=8,OF=BE=4.
∴AF=10﹣4=6.
在Rt△AFB中,
过点C作CG⊥x轴于点G,与FB的延长线交于点H.
∵∠ABC=90°=∠AFB=∠BHC
∴∠ABF+∠CBH=90°,∠ABF=∠BCH,∠FAB=∠CBH,
∴△ABF≌△BCH.
∴BH=AF=6,CH=BF=8.
∴AB==10,
∴OG=FH=8+6=14,CG=8+4=12.
∴所求C点的坐标为(14,12);
(3)当点P在AB上时,若OP=PQ,则ON=NQ,
∵△APM∽△ABF,AP=t,AB=10,BF=8,
∴ON=PM=t,
又∵ON=OQ=(t+1),
∴t=(t+1),
解得:t=
,
当点P在BC上时,t的值不存在.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
