2020-2021学年北师大版八年级数学下册 第1章三角形的证明 优生辅导训练题(word解析版)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册 第1章三角形的证明 优生辅导训练题(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 00:00:00 | ||
图片预览



文档简介
2020-2021年北师大版八年级数学下册《第1章三角形的证明》优生辅导训练题(附答案)
1.等腰三角形的一个角比另一个角2倍少20度,等腰三角形顶角的度数是( )
A.140°或44°或80°
B.20°或80°
C.44°或80°
D.140°
2.如图,△ABC中,∠A=36°,∠C=72°,BD平分∠ABC,ED∥BC,则图中等腰三角形的个数是( )
A.3
B.4
C.5
D.6
3.在三角形的内部,到三边距离相等的点是三角形的三条( )
A.中线的交点
B.角平分线的交点
C.高的交点
D.以上都不对
4.下列说法中,正确的有( )
①等腰三角形的底角一定是锐角.
②等腰三角形的角平分线、中线和高是同一条线段.
③等腰三角形两腰上的高相等.
④等腰三角形两腰上的中线相等.
A.0个
B.1个
C.2个
D.3个
5.元旦联欢会上,同学们玩抢凳子游戏,在与A、B、C三名同学距离相等的位置放一个凳子,谁先抢到凳子谁获胜.如果将A、B、C三名同学所在位置看作△ABC的三个顶点,那么凳子应该放在△ABC的( )
A.三边中线的交点
B.三条角平分线的交点
C.三边上高的交点
D.三边垂直平分线的交点
6.下列条件中,能判断两个直角三角形全等的是( )
A.有两条边分别相等
B.有一个锐角和一条边相等
C.有一条斜边相等
D.有一直角边和斜边上的高分别相等
7.下列说法错误的是( )
A.等腰三角形的高、中线、角平分线互相重合
B.三角形两边的垂直平分线的交点到三个顶点距离相等
C.等腰三角形的两个底角相等
D.等腰三角形顶角的外角是底角的二倍
8.如图所示,在△ABC中,CD,BE是两条高,那么图中与∠A相等的角的个数有( )
A.1个
B.2个
C.3个
D.4个
9.如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )
A.4.5
B.5
C.5.5
D.6
10.已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在格点上,位置如图,点C也在格点上,且△ABC为等腰三角形,则点C的个数为( )
A.7
B.8
C.9
D.10
11.如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A.90°
B.95°
C.100°
D.105°
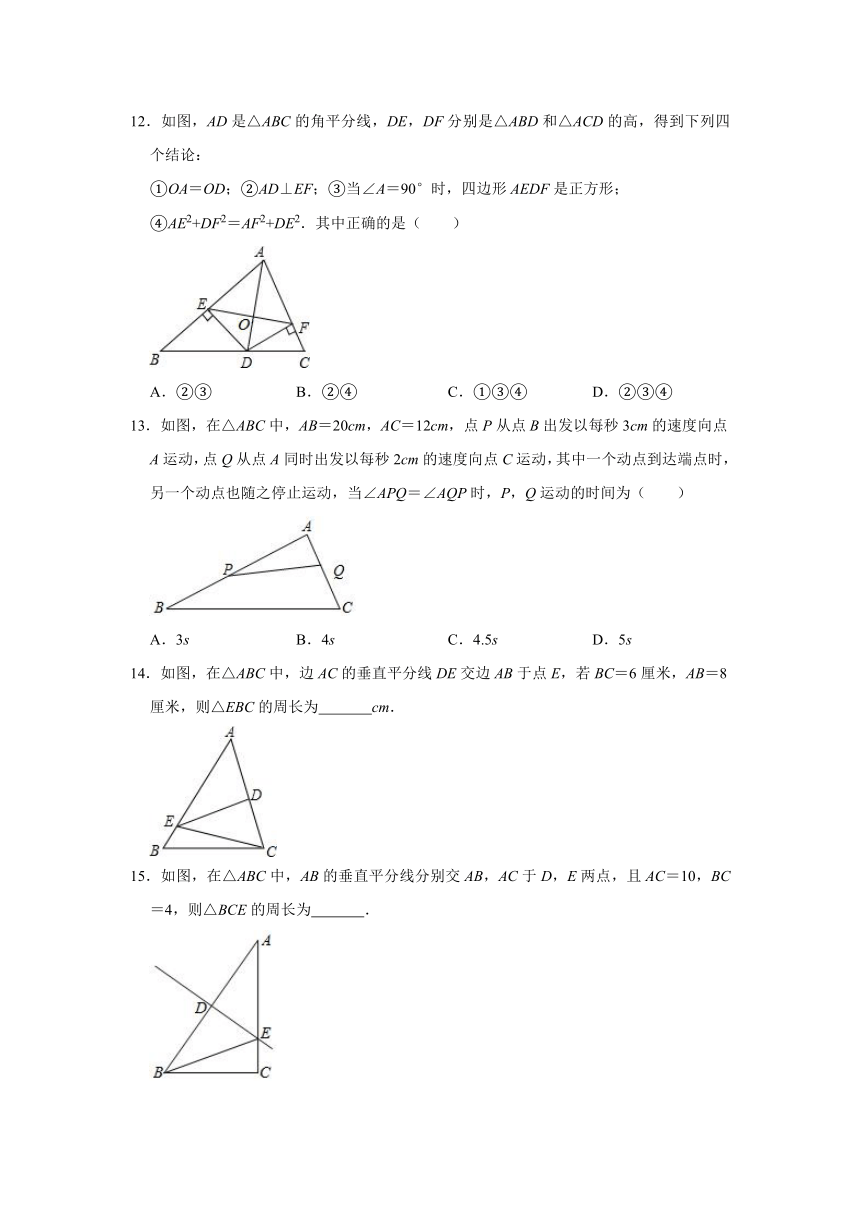
12.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:
①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;
④AE2+DF2=AF2+DE2.其中正确的是( )
A.②③
B.②④
C.①③④
D.②③④
13.如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当∠APQ=∠AQP时,P,Q运动的时间为( )
A.3s
B.4s
C.4.5s
D.5s
14.如图,在△ABC中,边AC的垂直平分线DE交边AB于点E,若BC=6厘米,AB=8厘米,则△EBC的周长为
cm.
15.如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为
.
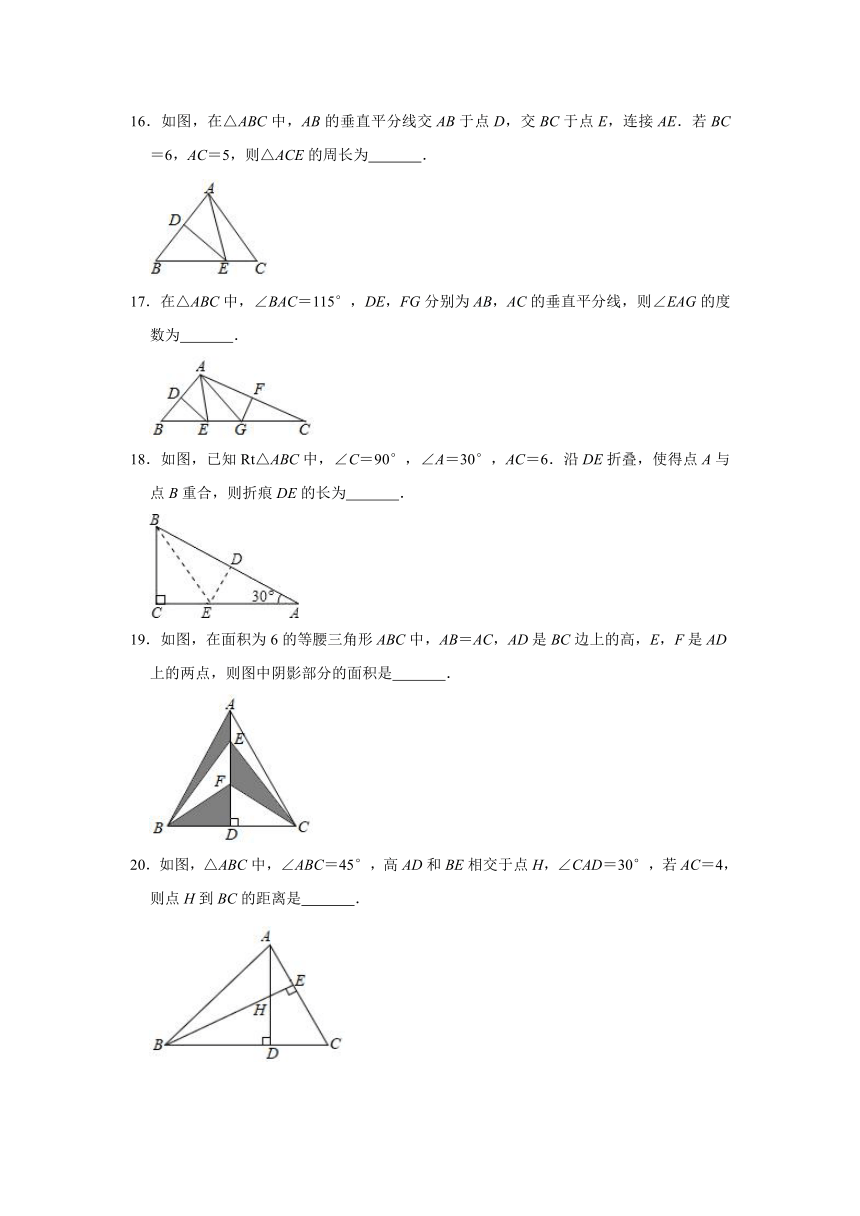
16.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为
.
17.在△ABC中,∠BAC=115°,DE,FG分别为AB,AC的垂直平分线,则∠EAG的度数为
.
18.如图,已知Rt△ABC中,∠C=90°,∠A=30°,AC=6.沿DE折叠,使得点A与点B重合,则折痕DE的长为
.
19.如图,在面积为6的等腰三角形ABC中,AB=AC,AD是BC边上的高,E,F是AD上的两点,则图中阴影部分的面积是
.
20.如图,△ABC中,∠ABC=45°,高AD和BE相交于点H,∠CAD=30°,若AC=4,则点H到BC的距离是
.
21.如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE=
°.
22.如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为
.
23.如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE=
.
24.如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是
秒.
25.如图,在△ABC中,AB=AC,D为线段BC上一动点(不与点B、C重合),连接AD,作∠DAE=∠BAC,且AD=AE,连接CE.
(1)如图1,当CE∥AB时,若∠BAD=35°,则∠DEC
度;
(2)如图2,设∠BAC=α(90°<α<180°),在点D运动过程中,当DE⊥BC时,∠DEC=
.(用含α的式子表示)
26.已知:如图,△ABC中,P、Q两点分别是边AB和AC的垂直平分线与BC的交点,连接AP和AQ,且BP=PQ=QC.
求∠C的度数.
证明:∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点,
∴PA=
,QC=QA.
∵BP=PQ=QC,
∴在△APQ中,PQ=
(等量代换)
∴△APQ是
三角形.
∴∠AQP=60°,
∵在△AQC中,QC=QA,
∴∠C=∠
.
又∵∠AQP是△AQC的外角,
∴∠AQP=∠
+∠
=60°.
(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠C=
.
27.如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长.
28.如图,将一张长方形的纸条ABCD沿EF折叠,若折叠后∠AGC′=48°,AD交EC′于点G.
(1)求∠CEF的度数;
(2)求证:△EFG是等腰三角形.
29.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
30.如图,四边形ABCD的对角线AC、BD相交于点O,∠ACB=∠ADB=90°,M为边AB的中点,连接MC,MD.
(1)求证:MC=MD;
(2)若△MCD是等边三角形,求∠AOB的度数.
31.如图,在△ABC中,∠B=90°,AB=8厘米,BC=6厘米,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动速度为1厘米/秒,点Q从点B开始沿B→C→A方向运动速度为2厘米/秒,若它们同时出发,设出发的时间为t秒.
(1)求出发2秒后,PQ的长;
(2)点Q在CA边上运动时,当△BCQ成为等腰三角形时,求点Q的运动时间.
32.在△ABC中,∠BAC>90°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F.
(1)若AB=AC,∠BAC=120°,求证BM=MN=NC;
(2)由(1)可知△AMN是
三角形;
(3)去掉(1)中的“∠BAC=120°”的条件,其他不变,判断△AMN的形状,并证明你的结论;
(4)当∠B与∠C满足怎样的数量关系时,△AMN是等腰三角形?直接写出所有可能的情况.
参考答案
1.解:设另一个角是x,表示出一个角是2x﹣20°,
①x是顶角,2x﹣20°是底角时,x+2(2x﹣20°)=180°,
解得x=44°,
所以,顶角是44°;
②x是底角,2x﹣20°是顶角时,2x+(2x﹣20°)=180°,
解得x=50°,
所以,顶角是2×50°﹣20°=80°;
③x与2x﹣20°都是底角时,x=2x﹣20°,
解得x=20°,
所以,顶角是180°﹣20°×2=140°;
综上所述,这个等腰三角形的顶角度数是44°或80°或140°.
故选:A.
2.解:∵∠A=36°,∠C=72°,
∴∠ABC=180°﹣72°﹣36°=72°,
∴∠ABC=∠C,
∴△ABC是等腰三角形,
∵DE∥BC,
∴∠AED=∠ABC,∠ADE=∠C,
∴∠AED=∠ADE,
∴△AED是等腰三角形,
∵BD平分∠ABC,
∴∠ABD=∠DBC=36°,
∴∠A=∠ABD=36°,∠EDB=∠EBD=36°,
∴△ABD,△BDE都是等腰三角形,
∵∠C=∠BDC=72°,
∴△BDC是等腰三角形,
∴等腰三角形有5个,
故选:C.
3.解:在三角形内部到三边距离相等的点是三个内角平分线的交点,
故选:B.
4.解:①等腰三角形的底角一定是锐角是正确的;
②等腰三角形的角平分线、中线和高不一定是同一条线段,原来的说法错误;
③等腰三角形两腰上的高相等是正确的;
④等腰三角形两腰上的中线相等是正确的.
故正确的有3个.
故选:D.
5.解:∵三角形的三条垂直平分线的交点到三角形三个顶点的距离相等,
∴凳子应放在△ABC的三条垂直平分线的交点最合适.
故选:D.
6.解:A、两边分别相等,但是不一定是对应边,不能判定两直角三角形全等,故此选项不符合题意;
B、一条边和一锐角对应相等,不能判定两直角三角形全等,故此选项不符合题意;
C、有一条斜边相等,两直角边不一定对应相等,不能判定两直角三角形全等,故此选项不符合题意;
D、有一条直角边和斜边上的高对应相等的两个直角三角形全等,故此选项符合题意;
故选:D.
7.解:A、等腰三角形底边上的高、底边上的中线、顶角的角平分线互相重合,故A错误;
B、三角形两边的垂直平分线的交点到三个顶点的距离相等,故B正确;
C、等腰三角形的两个底角相等,故C正确;
D、等腰三角形顶角的外角是底角的二倍,故D正确,
故选:A.
8.解:∵CD⊥AB,
∴∠CDA=∠BDH=90°,
∴∠A+∠DCA=90°,∠ABE+∠BHD=90°,
∵BE⊥AC,
∴∠A+∠ABE=90°,∠CHE+∠HCE=90°,
∴∠A=∠BHD=∠CHE,
故选:B.
9.解:∵△ABC是等腰三角形,D为底边的中点,
∴AD⊥BC,∠BAD=∠CAD,
∵∠BAC=120°,
∴∠BAD=60°,∠ADB=90°,
∵AE是∠BAD的角平分线,
∴∠DAE=∠EAB=30°.
∵DF∥AB,
∴∠F=∠BAE=30°.
∴∠DAF=∠F=30°,
∴AD=DF.
∵AB=11,∠B=30°,
∴AD=5.5,
∴DF=5.5
故选:C.
10.解:①以AB为底边,符合点C的有5个;
②以AB为腰,符合点C的有4个.所以符合条件的点C共有9个.故选:C.
11.解:∵CD=AC,∠A=50°,
∴∠ADC=∠A=50°,
根据题意得:MN是BC的垂直平分线,
∴CD=BD,
∴∠BCD=∠B,
∴∠B=∠ADC=25°,
∴∠ACB=180°﹣∠A﹣∠B=105°.
故选:D.
12.解:如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,
∴①不正确;
∵AD是△ABC的角平分线,
∴∠EAD∠FAD,
在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE2+DF2=AF2+DE2,
∴④正确;
在△AEO和△AFO中,
,
∴△AE0≌△AF0(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,
∴②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,
∴③正确.
综上,可得
正确的是:②③④.
故选:D.
13.解:设当∠APQ=∠AQP时,P,Q运动的时间为t秒,
∵∠APQ=∠AQP,
∴AP=AQ,
∴20﹣3t=2t,
解得t=4,
故选:B.
14.解:∵DE是边AC的垂直平分线,
∴EA=EC,
∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+AB=14(厘米),
故答案为:14.
15.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∴△BCE的周长=EB+EC+BC=EA+EC+BC=AC+BC=14,
故答案为:14.
16.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∴△ACE的周长=EA+EC+AC=EB+EC+AC=BC+AC=11,
故答案为:11.
17.解:∵∠BAC=115°,
∴∠B+∠C=180°﹣115°=65°,
∵DE,FG分别为AB,AC的垂直平分线,
∴EA=EB,GA=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=65°,
∴∠EAG=∠BAC﹣(∠EAB+∠GAC)=50°,
故答案为:50°.
18.解:由题意可得,BE平分∠ABC,DE=CE
又∠A=30°,AC=6
可得DE=AE
∴DE=(6﹣DE)
则DE=2.
故答案为2.
19.解:∵△ABC为等腰三角形,AD⊥BC,
∴BD=DC,
∵S△EFC=EF?CD,S△EFB=EF?BD,
∴S△EFC=S△EFB,
∴S阴影=S△ABD=S△ABC,
∵S△ABC=6,
∴S阴影=3.
故答案为:3.
20.解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠HBD+∠BHD=90°,
∵∠CAD=30°,AC=4,
∴CD=AC=2,
∵BE⊥AC,
∴∠HBD+∠C=90°,
∴∠BHD=∠C,
∵∠ABD=45°,
∴∠BAD=45°,
∴BD=AD,
在△BDH和△ADC中,
,
∴△BDH≌△ADC(AAS),
∴HD=CD=2,
故点H到BC的距离是2.
故答案为2.
21.解:∵AB=AC,∠A=50°,
∴∠ACB=∠ABC=(180°﹣50°)=65°,
∵将△ABC折叠,使点A落在点B处,折痕为DE,∠A=50°,
∴∠ABE=∠A=50°,
∴∠CBE=∠ABC﹣∠ABE=65°﹣50°=15°.
故答案为:15.
22.解:∵DE是BC边上的垂直平分线,
∴BE=CE.
∵△EDC的周长为24,
∴ED+DC+EC=24,①
∵△ABC与四边形AEDC的周长之差为12,
∴(AB+AC+BC)﹣(AE+ED+DC+AC)=(AB+AC+BC)﹣(AE+DC+AC)﹣DE=12,
∴BE+BD﹣DE=12,②
∵BE=CE,BD=DC,
∴①﹣②得,DE=6.
故答案为:6.
23.解:∵正方形ABCD的边长为4,对角线AC与BD相交于点O,
∴∠BAC=45°,AB∥DC,∠ADC=90°,
∵∠CAE=15°,
∴∠E=∠BAE=∠BAC﹣∠CAE=45°﹣15°=30°.
∵在Rt△ADE中,∠ADE=90°,∠E=30°,
∴AE=2AD=8.
故答案为8.
24.解:设运动的时间为x,
在△ABC中,AB=20cm,AC=12cm,
点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,
当△APQ是等腰三角形时,AP=AQ,
AP=20﹣3x,AQ=2x
即20﹣3x=2x,
解得x=4.
故答案为:4.
25.解:(1)∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠BAC=∠ACE,
∴∠BAC=∠B,
∴AC=BC,
∴△ABC是等边三角形,
∴∠BAC=∠DAE=∠ACB=∠ACE=60°,
∴△DAE是等边三角形,
∴∠AED=60°,
∴∠DEC=180°﹣35°﹣60°﹣60°=25°,
故答案为:25;
(2)连接CE,
∵∠BAC=α,AB=AC,
∴∠B=∠ACB=(180°﹣α)=90°﹣,
∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE=90°﹣,
∴∠DCE=2(90°﹣)=180°﹣α,
∵DE⊥BC,
∴∠CDE=90°,
∴∠DEC=90°﹣∠DCE=α﹣90°.
故答案为:α﹣90°.
26.证明:∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点,
∴PA=BP,QC=QA.
(垂直平分线上任意一点,到线段两端点的距离相等)
∵BP=PQ=QC,
∴在△APQ中,PQ=PA=QA(等量代换)
∴△APQ是等边三角形.
∴∠AQP=60°,
∵在△AQC中,QC=QA,
∴∠C=∠QAC.
又∵∠AQP是△AQC的外角,
∴∠AQP=∠C+∠QAC=60°.
(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠C=30°.
故答案为:BP,(垂直平分线上任意一点,到线段两端点的距离相等),PA=QA,等边,QAC,C,QAC,30°.
27.(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,
且BC=CA,
在△DBC和△ECA中,
∵
∴△DBC≌△ECA(AAS).
∴AE=CD.
(2)解:∵△CDB≌△AEC,
∴BD=CE,
∵AE是BC边上的中线,
∴BD=EC=BC=AC,且AC=12cm.
∴BD=6cm.
28.(1)解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BEG=∠AGC'=48°,
由折叠的性质得:∠CEF=∠C'EF,
∴∠CEF=(180°﹣48°)=66°;
(2)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GFE=∠CEF,
由折叠的性质得:∠CEF=∠C'EF,
∴∠GFE=∠C'EF,
∴GE=GF,
即△EFG是等腰三角形.
29.解:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
30.(1)证明:∵∠ACB=∠ADB=90°,M为边AB的中点,
∴MC=AB,MD=AB,
∴MC=MD;
(2)解:∵MC=MD=AB=AM=BM,
∴∠BAC=∠ACM,∠ABD=∠BDM,
∴∠BMC=2∠BAC,∠AMD=2∠ABD,
∵△MCD是等边三角形,
∴∠DMC=60°,
∴∠BMC+∠AMD=120°,
∴2∠BAC+2∠ABD=120°,
∴∠BAO+∠ABO=60°,
∴∠AOB=180°﹣60°=120°.
31.(1)解:(1)BQ=2×2=4cm,
BP=AB﹣AP=8﹣2×1=6cm,
∵∠B=90°,
PQ==2(cm);
(2)解:分三种情况:
①当CQ=BQ时,如图1所示:
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ
∴BQ=AQ,
∴CQ=AQ=5,
∴BC+CQ=11,
∴t=11÷2=5.5秒.
②当CQ=BC时,如图2所示:
则BC+CQ=12
∴t=12÷2=6秒.
③当BC=BQ时,如图3所示:
过B点作BE⊥AC于点E,
则BE===4.8(cm)
∴CE==3.6cm,
∴CQ=2CE=7.2cm,
∴BC+CQ=13.2cm,
∴t=13.2÷2=6.6秒.
由上可知,当t为5.5秒或6秒或6.6秒时,
△BCQ为等腰三角形.
32.(1)证明:连接AM、AN,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵ME是线段AB的垂直平分线,
∴MA=MB,
∴∠MAB=∠B=30°,
∴∠AMN=∠B+∠MAB=60°,
同理,NA=NC,
∴∠NAC=∠C=30°,
∴∠ANM=∠C+∠NAC=60°,
∴△AMN为等边三角形,
∴AM=MN=AN,
∴BM=MN=NC;
(2)解:由(1)可知△AMN是等边三角形,
故答案为:等边;
(3)解:△AMN是等腰三角形,
理由如下:∵AB=AC,
∴∠B=∠C,
∵∠MAB=∠B,∠AMN=∠B+∠MAB,∠NAC=∠C,∠ANM=∠C+∠NAC,
∴∠AMN=∠ANM,
∴AM=AN,
∴△AMN是等腰三角形;
(4)解:当∠B=∠C时,AM=AN;
当2∠B+∠C=90°时,∠MAC=90°,
∴NF∥MA,
∵CF=FA,
∴CN=CM,
∴NA=CM=MN,
同理,当∠B+2∠C=90°时,MA=MN,
综上所述,当∠B=∠C、2∠B+∠C=90°、∠B+2∠C=90°时,△AMN是等腰三角形.
1.等腰三角形的一个角比另一个角2倍少20度,等腰三角形顶角的度数是( )
A.140°或44°或80°
B.20°或80°
C.44°或80°
D.140°
2.如图,△ABC中,∠A=36°,∠C=72°,BD平分∠ABC,ED∥BC,则图中等腰三角形的个数是( )
A.3
B.4
C.5
D.6
3.在三角形的内部,到三边距离相等的点是三角形的三条( )
A.中线的交点
B.角平分线的交点
C.高的交点
D.以上都不对
4.下列说法中,正确的有( )
①等腰三角形的底角一定是锐角.
②等腰三角形的角平分线、中线和高是同一条线段.
③等腰三角形两腰上的高相等.
④等腰三角形两腰上的中线相等.
A.0个
B.1个
C.2个
D.3个
5.元旦联欢会上,同学们玩抢凳子游戏,在与A、B、C三名同学距离相等的位置放一个凳子,谁先抢到凳子谁获胜.如果将A、B、C三名同学所在位置看作△ABC的三个顶点,那么凳子应该放在△ABC的( )
A.三边中线的交点
B.三条角平分线的交点
C.三边上高的交点
D.三边垂直平分线的交点
6.下列条件中,能判断两个直角三角形全等的是( )
A.有两条边分别相等
B.有一个锐角和一条边相等
C.有一条斜边相等
D.有一直角边和斜边上的高分别相等
7.下列说法错误的是( )
A.等腰三角形的高、中线、角平分线互相重合
B.三角形两边的垂直平分线的交点到三个顶点距离相等
C.等腰三角形的两个底角相等
D.等腰三角形顶角的外角是底角的二倍
8.如图所示,在△ABC中,CD,BE是两条高,那么图中与∠A相等的角的个数有( )
A.1个
B.2个
C.3个
D.4个
9.如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )
A.4.5
B.5
C.5.5
D.6
10.已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在格点上,位置如图,点C也在格点上,且△ABC为等腰三角形,则点C的个数为( )
A.7
B.8
C.9
D.10
11.如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A.90°
B.95°
C.100°
D.105°
12.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:
①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;
④AE2+DF2=AF2+DE2.其中正确的是( )
A.②③
B.②④
C.①③④
D.②③④
13.如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当∠APQ=∠AQP时,P,Q运动的时间为( )
A.3s
B.4s
C.4.5s
D.5s
14.如图,在△ABC中,边AC的垂直平分线DE交边AB于点E,若BC=6厘米,AB=8厘米,则△EBC的周长为
cm.
15.如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为
.
16.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为
.
17.在△ABC中,∠BAC=115°,DE,FG分别为AB,AC的垂直平分线,则∠EAG的度数为
.
18.如图,已知Rt△ABC中,∠C=90°,∠A=30°,AC=6.沿DE折叠,使得点A与点B重合,则折痕DE的长为
.
19.如图,在面积为6的等腰三角形ABC中,AB=AC,AD是BC边上的高,E,F是AD上的两点,则图中阴影部分的面积是
.
20.如图,△ABC中,∠ABC=45°,高AD和BE相交于点H,∠CAD=30°,若AC=4,则点H到BC的距离是
.
21.如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE=
°.
22.如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为
.
23.如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE=
.
24.如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是
秒.
25.如图,在△ABC中,AB=AC,D为线段BC上一动点(不与点B、C重合),连接AD,作∠DAE=∠BAC,且AD=AE,连接CE.
(1)如图1,当CE∥AB时,若∠BAD=35°,则∠DEC
度;
(2)如图2,设∠BAC=α(90°<α<180°),在点D运动过程中,当DE⊥BC时,∠DEC=
.(用含α的式子表示)
26.已知:如图,△ABC中,P、Q两点分别是边AB和AC的垂直平分线与BC的交点,连接AP和AQ,且BP=PQ=QC.
求∠C的度数.
证明:∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点,
∴PA=
,QC=QA.
∵BP=PQ=QC,
∴在△APQ中,PQ=
(等量代换)
∴△APQ是
三角形.
∴∠AQP=60°,
∵在△AQC中,QC=QA,
∴∠C=∠
.
又∵∠AQP是△AQC的外角,
∴∠AQP=∠
+∠
=60°.
(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠C=
.
27.如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:AE=CD;
(2)若AC=12cm,求BD的长.
28.如图,将一张长方形的纸条ABCD沿EF折叠,若折叠后∠AGC′=48°,AD交EC′于点G.
(1)求∠CEF的度数;
(2)求证:△EFG是等腰三角形.
29.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
30.如图,四边形ABCD的对角线AC、BD相交于点O,∠ACB=∠ADB=90°,M为边AB的中点,连接MC,MD.
(1)求证:MC=MD;
(2)若△MCD是等边三角形,求∠AOB的度数.
31.如图,在△ABC中,∠B=90°,AB=8厘米,BC=6厘米,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动速度为1厘米/秒,点Q从点B开始沿B→C→A方向运动速度为2厘米/秒,若它们同时出发,设出发的时间为t秒.
(1)求出发2秒后,PQ的长;
(2)点Q在CA边上运动时,当△BCQ成为等腰三角形时,求点Q的运动时间.
32.在△ABC中,∠BAC>90°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F.
(1)若AB=AC,∠BAC=120°,求证BM=MN=NC;
(2)由(1)可知△AMN是
三角形;
(3)去掉(1)中的“∠BAC=120°”的条件,其他不变,判断△AMN的形状,并证明你的结论;
(4)当∠B与∠C满足怎样的数量关系时,△AMN是等腰三角形?直接写出所有可能的情况.
参考答案
1.解:设另一个角是x,表示出一个角是2x﹣20°,
①x是顶角,2x﹣20°是底角时,x+2(2x﹣20°)=180°,
解得x=44°,
所以,顶角是44°;
②x是底角,2x﹣20°是顶角时,2x+(2x﹣20°)=180°,
解得x=50°,
所以,顶角是2×50°﹣20°=80°;
③x与2x﹣20°都是底角时,x=2x﹣20°,
解得x=20°,
所以,顶角是180°﹣20°×2=140°;
综上所述,这个等腰三角形的顶角度数是44°或80°或140°.
故选:A.
2.解:∵∠A=36°,∠C=72°,
∴∠ABC=180°﹣72°﹣36°=72°,
∴∠ABC=∠C,
∴△ABC是等腰三角形,
∵DE∥BC,
∴∠AED=∠ABC,∠ADE=∠C,
∴∠AED=∠ADE,
∴△AED是等腰三角形,
∵BD平分∠ABC,
∴∠ABD=∠DBC=36°,
∴∠A=∠ABD=36°,∠EDB=∠EBD=36°,
∴△ABD,△BDE都是等腰三角形,
∵∠C=∠BDC=72°,
∴△BDC是等腰三角形,
∴等腰三角形有5个,
故选:C.
3.解:在三角形内部到三边距离相等的点是三个内角平分线的交点,
故选:B.
4.解:①等腰三角形的底角一定是锐角是正确的;
②等腰三角形的角平分线、中线和高不一定是同一条线段,原来的说法错误;
③等腰三角形两腰上的高相等是正确的;
④等腰三角形两腰上的中线相等是正确的.
故正确的有3个.
故选:D.
5.解:∵三角形的三条垂直平分线的交点到三角形三个顶点的距离相等,
∴凳子应放在△ABC的三条垂直平分线的交点最合适.
故选:D.
6.解:A、两边分别相等,但是不一定是对应边,不能判定两直角三角形全等,故此选项不符合题意;
B、一条边和一锐角对应相等,不能判定两直角三角形全等,故此选项不符合题意;
C、有一条斜边相等,两直角边不一定对应相等,不能判定两直角三角形全等,故此选项不符合题意;
D、有一条直角边和斜边上的高对应相等的两个直角三角形全等,故此选项符合题意;
故选:D.
7.解:A、等腰三角形底边上的高、底边上的中线、顶角的角平分线互相重合,故A错误;
B、三角形两边的垂直平分线的交点到三个顶点的距离相等,故B正确;
C、等腰三角形的两个底角相等,故C正确;
D、等腰三角形顶角的外角是底角的二倍,故D正确,
故选:A.
8.解:∵CD⊥AB,
∴∠CDA=∠BDH=90°,
∴∠A+∠DCA=90°,∠ABE+∠BHD=90°,
∵BE⊥AC,
∴∠A+∠ABE=90°,∠CHE+∠HCE=90°,
∴∠A=∠BHD=∠CHE,
故选:B.
9.解:∵△ABC是等腰三角形,D为底边的中点,
∴AD⊥BC,∠BAD=∠CAD,
∵∠BAC=120°,
∴∠BAD=60°,∠ADB=90°,
∵AE是∠BAD的角平分线,
∴∠DAE=∠EAB=30°.
∵DF∥AB,
∴∠F=∠BAE=30°.
∴∠DAF=∠F=30°,
∴AD=DF.
∵AB=11,∠B=30°,
∴AD=5.5,
∴DF=5.5
故选:C.
10.解:①以AB为底边,符合点C的有5个;
②以AB为腰,符合点C的有4个.所以符合条件的点C共有9个.故选:C.
11.解:∵CD=AC,∠A=50°,
∴∠ADC=∠A=50°,
根据题意得:MN是BC的垂直平分线,
∴CD=BD,
∴∠BCD=∠B,
∴∠B=∠ADC=25°,
∴∠ACB=180°﹣∠A﹣∠B=105°.
故选:D.
12.解:如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,
∴①不正确;
∵AD是△ABC的角平分线,
∴∠EAD∠FAD,
在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE2+DF2=AF2+DE2,
∴④正确;
在△AEO和△AFO中,
,
∴△AE0≌△AF0(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,
∴②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,
∴③正确.
综上,可得
正确的是:②③④.
故选:D.
13.解:设当∠APQ=∠AQP时,P,Q运动的时间为t秒,
∵∠APQ=∠AQP,
∴AP=AQ,
∴20﹣3t=2t,
解得t=4,
故选:B.
14.解:∵DE是边AC的垂直平分线,
∴EA=EC,
∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+AB=14(厘米),
故答案为:14.
15.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∴△BCE的周长=EB+EC+BC=EA+EC+BC=AC+BC=14,
故答案为:14.
16.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∴△ACE的周长=EA+EC+AC=EB+EC+AC=BC+AC=11,
故答案为:11.
17.解:∵∠BAC=115°,
∴∠B+∠C=180°﹣115°=65°,
∵DE,FG分别为AB,AC的垂直平分线,
∴EA=EB,GA=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=65°,
∴∠EAG=∠BAC﹣(∠EAB+∠GAC)=50°,
故答案为:50°.
18.解:由题意可得,BE平分∠ABC,DE=CE
又∠A=30°,AC=6
可得DE=AE
∴DE=(6﹣DE)
则DE=2.
故答案为2.
19.解:∵△ABC为等腰三角形,AD⊥BC,
∴BD=DC,
∵S△EFC=EF?CD,S△EFB=EF?BD,
∴S△EFC=S△EFB,
∴S阴影=S△ABD=S△ABC,
∵S△ABC=6,
∴S阴影=3.
故答案为:3.
20.解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠HBD+∠BHD=90°,
∵∠CAD=30°,AC=4,
∴CD=AC=2,
∵BE⊥AC,
∴∠HBD+∠C=90°,
∴∠BHD=∠C,
∵∠ABD=45°,
∴∠BAD=45°,
∴BD=AD,
在△BDH和△ADC中,
,
∴△BDH≌△ADC(AAS),
∴HD=CD=2,
故点H到BC的距离是2.
故答案为2.
21.解:∵AB=AC,∠A=50°,
∴∠ACB=∠ABC=(180°﹣50°)=65°,
∵将△ABC折叠,使点A落在点B处,折痕为DE,∠A=50°,
∴∠ABE=∠A=50°,
∴∠CBE=∠ABC﹣∠ABE=65°﹣50°=15°.
故答案为:15.
22.解:∵DE是BC边上的垂直平分线,
∴BE=CE.
∵△EDC的周长为24,
∴ED+DC+EC=24,①
∵△ABC与四边形AEDC的周长之差为12,
∴(AB+AC+BC)﹣(AE+ED+DC+AC)=(AB+AC+BC)﹣(AE+DC+AC)﹣DE=12,
∴BE+BD﹣DE=12,②
∵BE=CE,BD=DC,
∴①﹣②得,DE=6.
故答案为:6.
23.解:∵正方形ABCD的边长为4,对角线AC与BD相交于点O,
∴∠BAC=45°,AB∥DC,∠ADC=90°,
∵∠CAE=15°,
∴∠E=∠BAE=∠BAC﹣∠CAE=45°﹣15°=30°.
∵在Rt△ADE中,∠ADE=90°,∠E=30°,
∴AE=2AD=8.
故答案为8.
24.解:设运动的时间为x,
在△ABC中,AB=20cm,AC=12cm,
点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,
当△APQ是等腰三角形时,AP=AQ,
AP=20﹣3x,AQ=2x
即20﹣3x=2x,
解得x=4.
故答案为:4.
25.解:(1)∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠BAC=∠ACE,
∴∠BAC=∠B,
∴AC=BC,
∴△ABC是等边三角形,
∴∠BAC=∠DAE=∠ACB=∠ACE=60°,
∴△DAE是等边三角形,
∴∠AED=60°,
∴∠DEC=180°﹣35°﹣60°﹣60°=25°,
故答案为:25;
(2)连接CE,
∵∠BAC=α,AB=AC,
∴∠B=∠ACB=(180°﹣α)=90°﹣,
∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE=90°﹣,
∴∠DCE=2(90°﹣)=180°﹣α,
∵DE⊥BC,
∴∠CDE=90°,
∴∠DEC=90°﹣∠DCE=α﹣90°.
故答案为:α﹣90°.
26.证明:∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点,
∴PA=BP,QC=QA.
(垂直平分线上任意一点,到线段两端点的距离相等)
∵BP=PQ=QC,
∴在△APQ中,PQ=PA=QA(等量代换)
∴△APQ是等边三角形.
∴∠AQP=60°,
∵在△AQC中,QC=QA,
∴∠C=∠QAC.
又∵∠AQP是△AQC的外角,
∴∠AQP=∠C+∠QAC=60°.
(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠C=30°.
故答案为:BP,(垂直平分线上任意一点,到线段两端点的距离相等),PA=QA,等边,QAC,C,QAC,30°.
27.(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,
且BC=CA,
在△DBC和△ECA中,
∵
∴△DBC≌△ECA(AAS).
∴AE=CD.
(2)解:∵△CDB≌△AEC,
∴BD=CE,
∵AE是BC边上的中线,
∴BD=EC=BC=AC,且AC=12cm.
∴BD=6cm.
28.(1)解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BEG=∠AGC'=48°,
由折叠的性质得:∠CEF=∠C'EF,
∴∠CEF=(180°﹣48°)=66°;
(2)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠GFE=∠CEF,
由折叠的性质得:∠CEF=∠C'EF,
∴∠GFE=∠C'EF,
∴GE=GF,
即△EFG是等腰三角形.
29.解:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
30.(1)证明:∵∠ACB=∠ADB=90°,M为边AB的中点,
∴MC=AB,MD=AB,
∴MC=MD;
(2)解:∵MC=MD=AB=AM=BM,
∴∠BAC=∠ACM,∠ABD=∠BDM,
∴∠BMC=2∠BAC,∠AMD=2∠ABD,
∵△MCD是等边三角形,
∴∠DMC=60°,
∴∠BMC+∠AMD=120°,
∴2∠BAC+2∠ABD=120°,
∴∠BAO+∠ABO=60°,
∴∠AOB=180°﹣60°=120°.
31.(1)解:(1)BQ=2×2=4cm,
BP=AB﹣AP=8﹣2×1=6cm,
∵∠B=90°,
PQ==2(cm);
(2)解:分三种情况:
①当CQ=BQ时,如图1所示:
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∠A+∠C=90°,
∴∠A=∠ABQ
∴BQ=AQ,
∴CQ=AQ=5,
∴BC+CQ=11,
∴t=11÷2=5.5秒.
②当CQ=BC时,如图2所示:
则BC+CQ=12
∴t=12÷2=6秒.
③当BC=BQ时,如图3所示:
过B点作BE⊥AC于点E,
则BE===4.8(cm)
∴CE==3.6cm,
∴CQ=2CE=7.2cm,
∴BC+CQ=13.2cm,
∴t=13.2÷2=6.6秒.
由上可知,当t为5.5秒或6秒或6.6秒时,
△BCQ为等腰三角形.
32.(1)证明:连接AM、AN,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵ME是线段AB的垂直平分线,
∴MA=MB,
∴∠MAB=∠B=30°,
∴∠AMN=∠B+∠MAB=60°,
同理,NA=NC,
∴∠NAC=∠C=30°,
∴∠ANM=∠C+∠NAC=60°,
∴△AMN为等边三角形,
∴AM=MN=AN,
∴BM=MN=NC;
(2)解:由(1)可知△AMN是等边三角形,
故答案为:等边;
(3)解:△AMN是等腰三角形,
理由如下:∵AB=AC,
∴∠B=∠C,
∵∠MAB=∠B,∠AMN=∠B+∠MAB,∠NAC=∠C,∠ANM=∠C+∠NAC,
∴∠AMN=∠ANM,
∴AM=AN,
∴△AMN是等腰三角形;
(4)解:当∠B=∠C时,AM=AN;
当2∠B+∠C=90°时,∠MAC=90°,
∴NF∥MA,
∵CF=FA,
∴CN=CM,
∴NA=CM=MN,
同理,当∠B+2∠C=90°时,MA=MN,
综上所述,当∠B=∠C、2∠B+∠C=90°、∠B+2∠C=90°时,△AMN是等腰三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
