2020-2021学年八年级数学人教版下册:19..2.2一次函数课件(共44张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册:19..2.2一次函数课件(共44张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 994.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 19:40:06 | ||
图片预览





文档简介
(共44张PPT)
19.2一次函数(2)
?
1.一次函数的图象有什么性质?
2.一次函数和正比例函数之间有什么联系?
学习目标
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
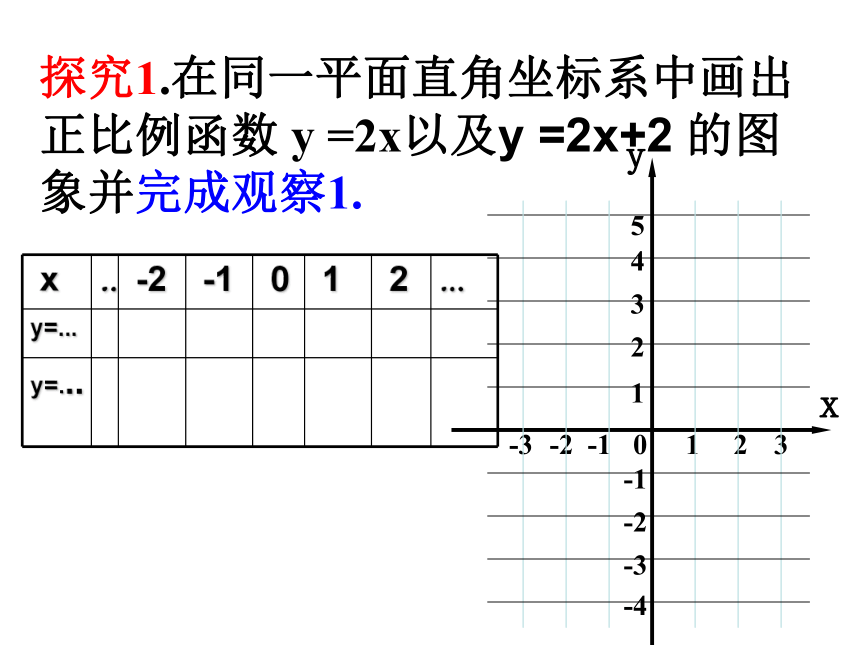
探究1.在同一平面直角坐标系中画出正比例函数
y
=2x以及y
=2x+2
的图象并完成观察1.
x
…
-2
-1
0
1
2
…
y=...
y=...
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
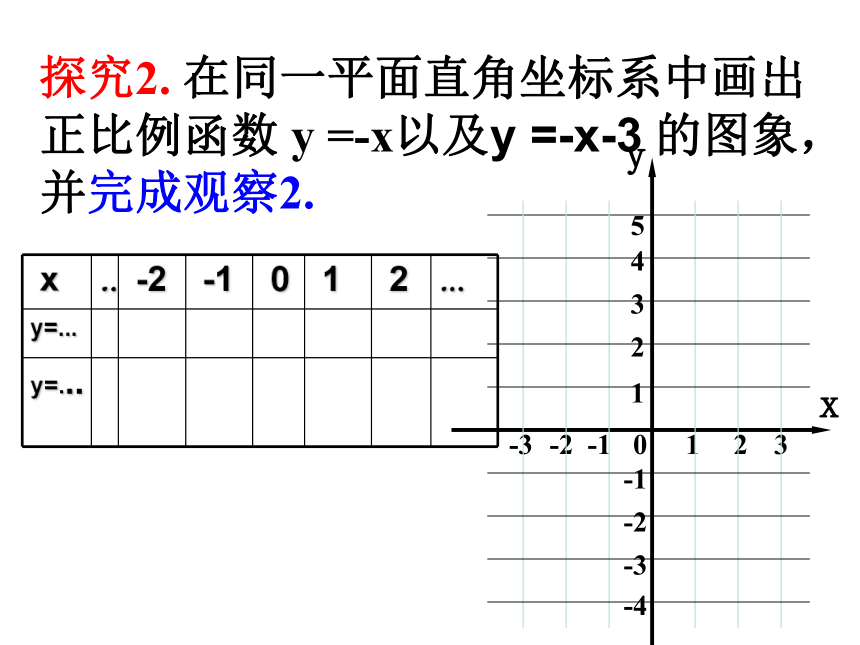
探究2.
在同一平面直角坐标系中画出正比例函数
y
=-x以及y
=-x-3
的图象,并完成观察2.
x
…
-2
-1
0
1
2
…
y=...
y=...
一般地,一次函数y=kx+b(k、b是常数,k≠0)的图象,是一条_______;
直线y=kx+b与y轴交于(___,___)
即可以看作由直线y=_______平移______个单位长度而得,
(当b>0,向____平移,当b<0,向____平移)
当k>0,y随x
增大而________
;当k<0,y随x增大而_____________。
直线
归纳:
0
b
kx
lbl
上
下
增大
减小
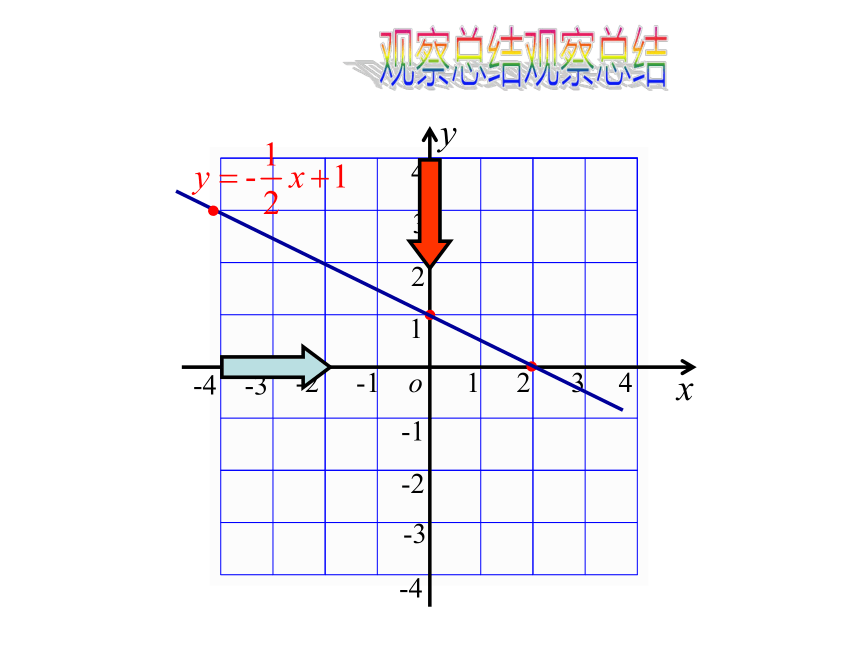
剖析y随x的增大而……
o
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
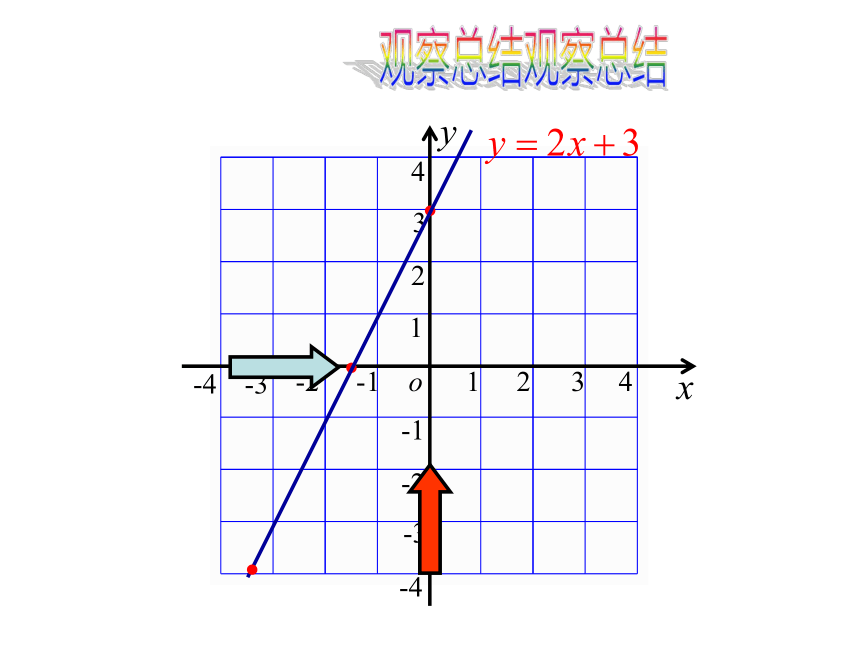
观察总结
o
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
观察总结
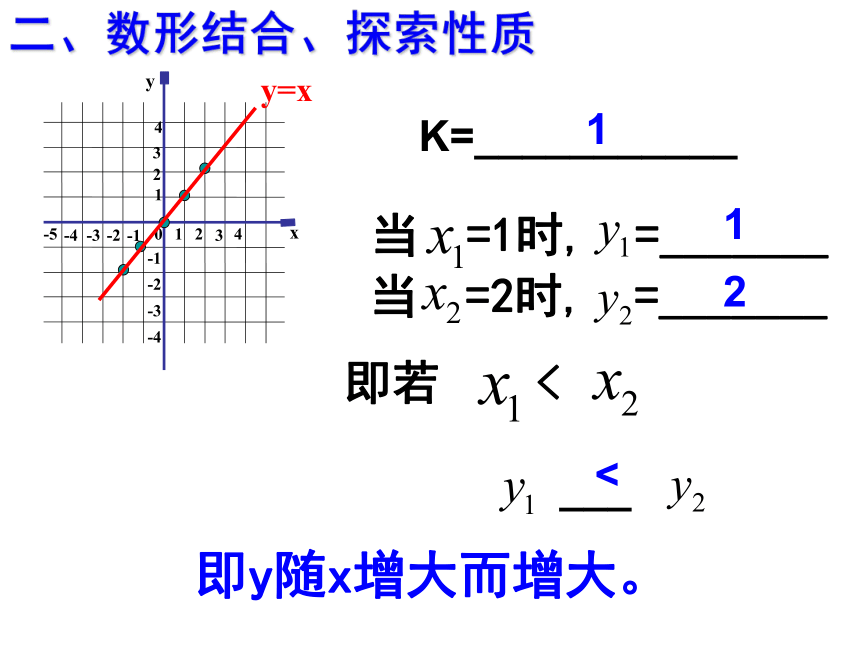
二、数形结合、探索性质
0
1
2
3
4
-5
-4
-3
-2
-1
1
2
3
4
-1
-2
-3
-4
x
y
y=x
K=___________
1
当
=2时,
=_______
当
=1时,
=_______
即若
<
___
1
2
<
即y随x增大而增大。
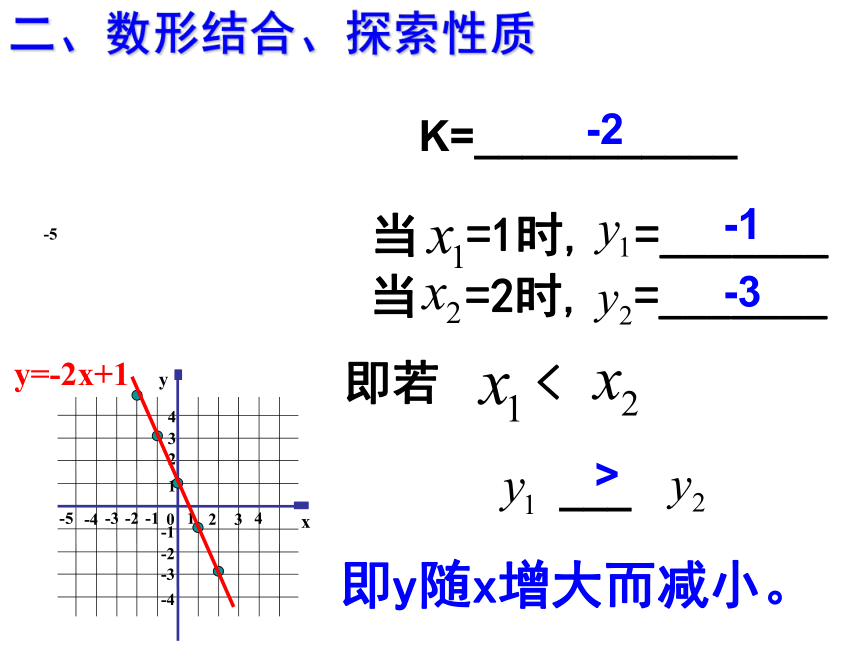
二、数形结合、探索性质
-5
0
1
2
3
4
-5
-4
-3
-2
-1
1
2
3
4
-1
-2
-3
-4
x
y
y=-2x+1
K=___________
-2
当
=2时,
=_______
当
=1时,
=_______
即若
<
___
-1
-3
>
即y随x增大而减小。
直线
y=3x-2可以由直线
y=3x向___平移
___个单位得到.
2
.
对于函数
y=
5x-6,y的值随x值的减小而_____.
3.
已知函数
y=(m
-3)x
-5;
⑴.当m为何值时y随x的增大而增大?
⑵.当m为何值时y随x的增大而减小?
下
2
减小
巩固练习
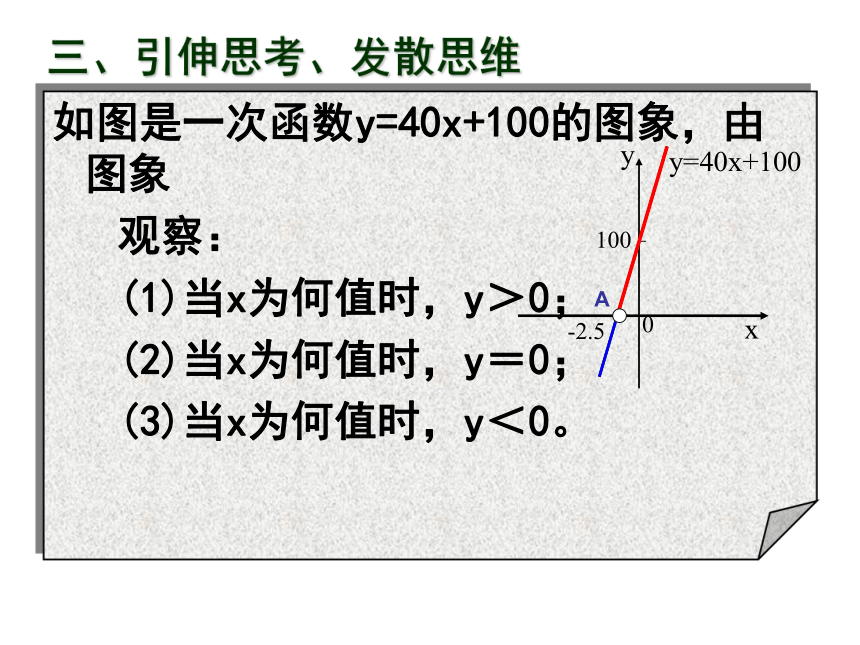
如图是一次函数y=40x+100的图象,由图象
观察:
(1)当x为何值时,y>0;
(2)当x为何值时,y=0;
(3)当x为何值时,y<0。
三、引伸思考、发散思维
0
-2.5
100
y=40x+100
x
y
A
随堂练习
A
1.直线
y
=3x-2过点(0,___),与直线
y
=3x__________(平行或相交),即直线
y
=3x-2可以看作由直线
y
=3x向___平移___个单位得到.
2.直线
y
=
5x-6经过(0,____),y随x的增大而_____
,若x1则y1_____y2(>、<、=)。
B
1.函数
y
=(m
-3)x
-5,y随x的增大而增大,则m=____,它的图像经过点(0,___)。
2.已知直线y=3x+1与y=(k-1)x平行,则k
的值为___________。
解析式上,一次函数y
=
kx
+
b与正比例函数y
=
kx只差一个常数
b,
图象上,又有怎样的关系?
复习巩固
埋设问题
K
>0
K<0
y
=
k
x(k≠0)
y
=
k
x
+
b
(k≠0)
?
x
y
=
kx
(K≠0)
y
=
-2x
y
=
-2x+1
直线y
=
-2x+1的位置如何?
把直线y
=
-2x向上平移1个单位长度。
o
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
探究1
与x轴的交点是_______.
与y轴的交点是_______.
从图像上看,直线
(2,0)
(0,
1)
从解析式上看,你能得出结论么?
请你完成探究1
一次函数
与x轴的交点
与y轴的交点
y=2x+2
(___,0)
(0,___)
y=-x-3
(___,0)
(0,___)
y=kx+b
(___,0)
(0,___)
-1
-3
2
-3
b
探究1
归纳1:一次函数y=kx+b(k≠0)的图象是一条________,作一次函数y=kx+b的图象可以用_________法,即过点(___,0)和(0,____),作一条直线即可。
直线
两点
b
归纳
一次函数y=kx+b的图像:
与x轴交点:
与y轴交点:
(
0
,
b
)
例:用简便方法画一次函数y
=
2x-1的图象。
y=2x-1
x
0
y=2x-1
0
-1
.
.
解:
探究2:在同一平面直角坐标系中作下列一次函数的图像(两点法):
y=2x+1
y=2x-1
y=-2x+1
y=-2x-1
k的值
b的值
经过的象限
y=2x+1
k=
b=
y=2x-1
k=
b=
y=-2x+1
k=
b=
y=-2x-1
k=
b=
2
1
一、二、三
-1
一、二、四
2
一、二、四
二、三、四
-2
1
-2
-1
(1)k>0,
(2)k>0,
(3)k<0,b>0
(4)k<0,b<0
0
x
y
(0,b)
x
y
0
(0,b)
经过一、二、三象限
经过一、三、四象限
0
x
y
(0,b)
0
x
y
(0,b)
经过一、二、四象限
经过二、三、四象限
b>0
b<0
归纳2:直线y=kx+b(k≠0)中,
k,b决定着直线的位置.
①k>0,b>0,直线经过_______象限;
②k>0,b<0,直线经过_______象限;
③k<0,b>0,直线经过_______象限;
④k<0,b<0,直线经过_______象限.
学会画草图!
巩固练习
1.函数y=3x+2的图象大致是(
)
y
x
0
A
x
0
B
y
x
0
C
y
x
0
D
y
B
2.y
=
x-3的图象与x、y轴分别交于A,B.
(1)则A,B的坐标分别是?
(2)三角形AOB的面积是?
y=x-3
.
.
巩固练习
A(3,0)
B(0,-3)
-1
1
-1
0
1
y=2x+1
y=2x
x
y
探究三
(0,1)
直线y=2x向上平移1个单位长度,得到直线___________,
直线y=2x+1与y轴的交点是________
它和b有什么关系?______________
y=2x+1
(0,1)
b=1
-1
1
-1
0
1
y=2x
y=2x-1
x
y
探究三
(0,-1)
直线y=2x向下平移1个单位长度,得到直线___________,
y=2x-1
直线y=2x-1与y轴的交点是________
它和b有什么关系?______________
(0,-1)
b=-1
请你完成探究3
归纳3
直线y=kx+b的图象与y轴交点的纵坐标就是______的值.
b
课后作业(表格)
y=kx+b
示意图
(草图)
直线经过
的象限
直线的
变化趋势
k>0
b=0
b>0
b<0
k<0
b=0
b>0
b<0
1.若正比例函数
y
=
kx
的图象,经过点(-1,-5),则这个函数解析式为
_________.
引入
若小明画了如图所示的一条直线,这条直线是什么函数?
x与y的函数关系式是什么?
确定正比例函数解析式需要几个条件?
正比例函数y=kx
过原点的直线是正比例函数。
若一次函数
y
=
kx
+
5
的图象平行于
,则
k=__;
3
y=3x
y=3x+4
若两直线平行,则k的值相等。
若一次函数
y
=
3x
+
b
的图象经过点A(0,5),则
b=__;
4
一次函数图象与y轴的交点可以确定b。
又有同学画了如下一条直线:
y
=
x
+
b
,
2
则
b=________
例
已知一次函数图象经过(3,4),(-6,-2)两点,求其解析式.
又有同学画了如下一条直线:
请你确定该直线的解析式。
确定一次函数解析式需要几个条件?
想一想、议一议
发现:在确定函数表达式时,要求几个
常数就需要知道几个点的坐标。
待定系数法
确定一次函数表达式的步骤:
1、设—设函数表达式y=kx+b
2、代—将已知条件代入y=kx+b中,列出关于k、b的方程
3、求—解方程,求k、b的值
4、写—把求出的k、b值代回到表达式中
直线y=5x-3的图象大致是(
)
D
复习旧知
请你确定该直线的解析式。
解:
假设一次函数为________
∵一次函数经过点
(__,__)与(__,__)
复习旧知
∴
2
-1
1
-4
请你确定该直线的解析式。
10
你能知道这条折线的解析式么?
10
14
下面,我们来共同学习~
y=5x
(x≧0)
“黄金一号”,种子
的价格为5元/千克,那么种子的价格y(单位:元)和重量x(单位:千克)之间的关系式?
如果一次购买2千克以上的种子,超过2千克部分的种子打8折,y=5x还成立么?
购买种子的数量/千克
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
2.5
5
7.5
10
12
14
18
16
(0≦x≦2)
填写下表:
购买种子数量与付款金额之间的函数关系式是什么?
解:设购买种子为x千克,付款金额为y元,
当0≦x≦2时
y=5x
当x>2时
y=0.8×5(x-2)+10
=4x+2
分段函数
y
=5x(0≦x≦2)
=4x+2(x>2)
图象如图
19.2一次函数(2)
?
1.一次函数的图象有什么性质?
2.一次函数和正比例函数之间有什么联系?
学习目标
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
探究1.在同一平面直角坐标系中画出正比例函数
y
=2x以及y
=2x+2
的图象并完成观察1.
x
…
-2
-1
0
1
2
…
y=...
y=...
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
探究2.
在同一平面直角坐标系中画出正比例函数
y
=-x以及y
=-x-3
的图象,并完成观察2.
x
…
-2
-1
0
1
2
…
y=...
y=...
一般地,一次函数y=kx+b(k、b是常数,k≠0)的图象,是一条_______;
直线y=kx+b与y轴交于(___,___)
即可以看作由直线y=_______平移______个单位长度而得,
(当b>0,向____平移,当b<0,向____平移)
当k>0,y随x
增大而________
;当k<0,y随x增大而_____________。
直线
归纳:
0
b
kx
lbl
上
下
增大
减小
剖析y随x的增大而……
o
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
观察总结
o
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
观察总结
二、数形结合、探索性质
0
1
2
3
4
-5
-4
-3
-2
-1
1
2
3
4
-1
-2
-3
-4
x
y
y=x
K=___________
1
当
=2时,
=_______
当
=1时,
=_______
即若
<
___
1
2
<
即y随x增大而增大。
二、数形结合、探索性质
-5
0
1
2
3
4
-5
-4
-3
-2
-1
1
2
3
4
-1
-2
-3
-4
x
y
y=-2x+1
K=___________
-2
当
=2时,
=_______
当
=1时,
=_______
即若
<
___
-1
-3
>
即y随x增大而减小。
直线
y=3x-2可以由直线
y=3x向___平移
___个单位得到.
2
.
对于函数
y=
5x-6,y的值随x值的减小而_____.
3.
已知函数
y=(m
-3)x
-5;
⑴.当m为何值时y随x的增大而增大?
⑵.当m为何值时y随x的增大而减小?
下
2
减小
巩固练习
如图是一次函数y=40x+100的图象,由图象
观察:
(1)当x为何值时,y>0;
(2)当x为何值时,y=0;
(3)当x为何值时,y<0。
三、引伸思考、发散思维
0
-2.5
100
y=40x+100
x
y
A
随堂练习
A
1.直线
y
=3x-2过点(0,___),与直线
y
=3x__________(平行或相交),即直线
y
=3x-2可以看作由直线
y
=3x向___平移___个单位得到.
2.直线
y
=
5x-6经过(0,____),y随x的增大而_____
,若x1
B
1.函数
y
=(m
-3)x
-5,y随x的增大而增大,则m=____,它的图像经过点(0,___)。
2.已知直线y=3x+1与y=(k-1)x平行,则k
的值为___________。
解析式上,一次函数y
=
kx
+
b与正比例函数y
=
kx只差一个常数
b,
图象上,又有怎样的关系?
复习巩固
埋设问题
K
>0
K<0
y
=
k
x(k≠0)
y
=
k
x
+
b
(k≠0)
?
x
y
=
kx
(K≠0)
y
=
-2x
y
=
-2x+1
直线y
=
-2x+1的位置如何?
把直线y
=
-2x向上平移1个单位长度。
o
1
2
3
4
-1
-2
-3
-4
1
2
3
4
-1
-2
-3
-4
探究1
与x轴的交点是_______.
与y轴的交点是_______.
从图像上看,直线
(2,0)
(0,
1)
从解析式上看,你能得出结论么?
请你完成探究1
一次函数
与x轴的交点
与y轴的交点
y=2x+2
(___,0)
(0,___)
y=-x-3
(___,0)
(0,___)
y=kx+b
(___,0)
(0,___)
-1
-3
2
-3
b
探究1
归纳1:一次函数y=kx+b(k≠0)的图象是一条________,作一次函数y=kx+b的图象可以用_________法,即过点(___,0)和(0,____),作一条直线即可。
直线
两点
b
归纳
一次函数y=kx+b的图像:
与x轴交点:
与y轴交点:
(
0
,
b
)
例:用简便方法画一次函数y
=
2x-1的图象。
y=2x-1
x
0
y=2x-1
0
-1
.
.
解:
探究2:在同一平面直角坐标系中作下列一次函数的图像(两点法):
y=2x+1
y=2x-1
y=-2x+1
y=-2x-1
k的值
b的值
经过的象限
y=2x+1
k=
b=
y=2x-1
k=
b=
y=-2x+1
k=
b=
y=-2x-1
k=
b=
2
1
一、二、三
-1
一、二、四
2
一、二、四
二、三、四
-2
1
-2
-1
(1)k>0,
(2)k>0,
(3)k<0,b>0
(4)k<0,b<0
0
x
y
(0,b)
x
y
0
(0,b)
经过一、二、三象限
经过一、三、四象限
0
x
y
(0,b)
0
x
y
(0,b)
经过一、二、四象限
经过二、三、四象限
b>0
b<0
归纳2:直线y=kx+b(k≠0)中,
k,b决定着直线的位置.
①k>0,b>0,直线经过_______象限;
②k>0,b<0,直线经过_______象限;
③k<0,b>0,直线经过_______象限;
④k<0,b<0,直线经过_______象限.
学会画草图!
巩固练习
1.函数y=3x+2的图象大致是(
)
y
x
0
A
x
0
B
y
x
0
C
y
x
0
D
y
B
2.y
=
x-3的图象与x、y轴分别交于A,B.
(1)则A,B的坐标分别是?
(2)三角形AOB的面积是?
y=x-3
.
.
巩固练习
A(3,0)
B(0,-3)
-1
1
-1
0
1
y=2x+1
y=2x
x
y
探究三
(0,1)
直线y=2x向上平移1个单位长度,得到直线___________,
直线y=2x+1与y轴的交点是________
它和b有什么关系?______________
y=2x+1
(0,1)
b=1
-1
1
-1
0
1
y=2x
y=2x-1
x
y
探究三
(0,-1)
直线y=2x向下平移1个单位长度,得到直线___________,
y=2x-1
直线y=2x-1与y轴的交点是________
它和b有什么关系?______________
(0,-1)
b=-1
请你完成探究3
归纳3
直线y=kx+b的图象与y轴交点的纵坐标就是______的值.
b
课后作业(表格)
y=kx+b
示意图
(草图)
直线经过
的象限
直线的
变化趋势
k>0
b=0
b>0
b<0
k<0
b=0
b>0
b<0
1.若正比例函数
y
=
kx
的图象,经过点(-1,-5),则这个函数解析式为
_________.
引入
若小明画了如图所示的一条直线,这条直线是什么函数?
x与y的函数关系式是什么?
确定正比例函数解析式需要几个条件?
正比例函数y=kx
过原点的直线是正比例函数。
若一次函数
y
=
kx
+
5
的图象平行于
,则
k=__;
3
y=3x
y=3x+4
若两直线平行,则k的值相等。
若一次函数
y
=
3x
+
b
的图象经过点A(0,5),则
b=__;
4
一次函数图象与y轴的交点可以确定b。
又有同学画了如下一条直线:
y
=
x
+
b
,
2
则
b=________
例
已知一次函数图象经过(3,4),(-6,-2)两点,求其解析式.
又有同学画了如下一条直线:
请你确定该直线的解析式。
确定一次函数解析式需要几个条件?
想一想、议一议
发现:在确定函数表达式时,要求几个
常数就需要知道几个点的坐标。
待定系数法
确定一次函数表达式的步骤:
1、设—设函数表达式y=kx+b
2、代—将已知条件代入y=kx+b中,列出关于k、b的方程
3、求—解方程,求k、b的值
4、写—把求出的k、b值代回到表达式中
直线y=5x-3的图象大致是(
)
D
复习旧知
请你确定该直线的解析式。
解:
假设一次函数为________
∵一次函数经过点
(__,__)与(__,__)
复习旧知
∴
2
-1
1
-4
请你确定该直线的解析式。
10
你能知道这条折线的解析式么?
10
14
下面,我们来共同学习~
y=5x
(x≧0)
“黄金一号”,种子
的价格为5元/千克,那么种子的价格y(单位:元)和重量x(单位:千克)之间的关系式?
如果一次购买2千克以上的种子,超过2千克部分的种子打8折,y=5x还成立么?
购买种子的数量/千克
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
2.5
5
7.5
10
12
14
18
16
(0≦x≦2)
填写下表:
购买种子数量与付款金额之间的函数关系式是什么?
解:设购买种子为x千克,付款金额为y元,
当0≦x≦2时
y=5x
当x>2时
y=0.8×5(x-2)+10
=4x+2
分段函数
y
=5x(0≦x≦2)
=4x+2(x>2)
图象如图
