2020-2021学年八年级数学人教版下册第17章勾股定理复习课件(共15张ppt)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第17章勾股定理复习课件(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 19:33:23 | ||
图片预览






文档简介
(共15张PPT)
勾股定理的复习课(1)
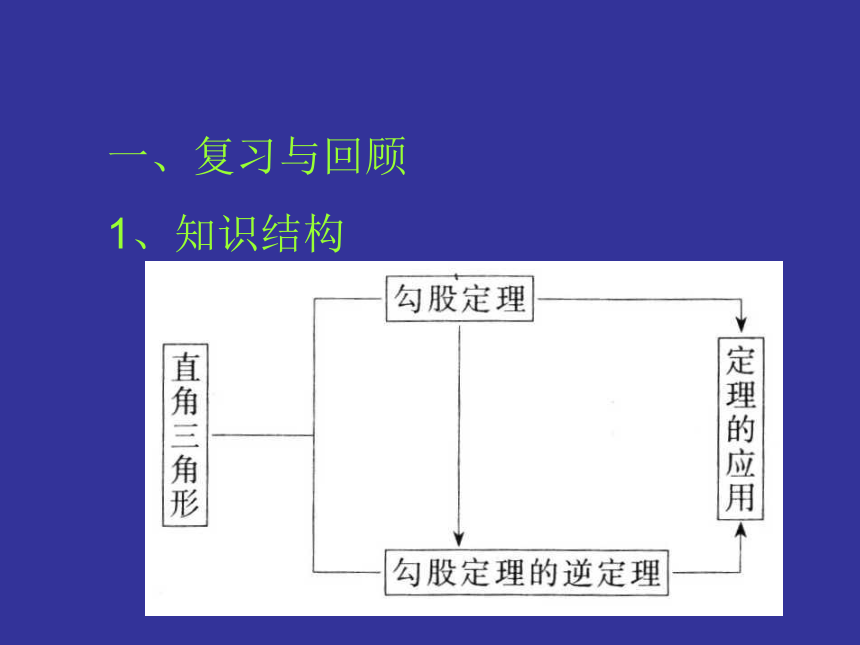
一、复习与回顾
1、知识结构
2、勾股定理及其逆定理的作用
(1)勾股定理揭示了直角三角形边与边之间的数量关系,是解决有关线段计算问题的重要依据.
勾股定理的直接作用是知道直角三角形任意两边的长度,求第三边的长.这里一定要注意找准斜边、直角边;二要熟悉公式的变形:
(2)“若三角形的两条边的平方和等于第三边的平方,则这个三角形为
直角三角形”这一定理是勾股定理的逆定理.它可以帮助我们判断三角形的形状.为根据边的关系解决角的有关问题提供了新的方法.
勾股定理的作用:
①已知直角三角形的两边,求第三边;
②在数轴上作出表示(n为正整数)的点.
3、勾股定理及其逆定理的区别
勾股定理的逆定理是用来判定一个三角形是否是直角三角形的,但在判定一个三角形是否是直角三角形时应首先确定该三角形的最大边,当其余两边的平方和等于最大边的平方时,该三角形才是直角三角形.勾股定理的逆定理也可用来证明两直线是否垂直。
勾股定理是直角三角形的性质定理,而勾股定理的逆定理是直角三角形的判定定理,它不仅可以判定三角形是否为直角三角形,还可以判定哪一个角是直角,从而产生了证明两直线互相垂直的新方法:利用勾股定理的逆定理,通过计算来证明,体现了数形结合的思想.
4、知识的扩展
三角形的三边分别为a、b、c,其中c为最大边,若
,则三角形是直角三角形;
若
,则三角形是锐角三角形;
若
,则三角形是钝角三角形.所以使用勾股定理的逆定理时首先要确定三角形的最大边.
二、典型例题讲解
例1:如果一个直角三角形的两条边长分别是6cm和8cm,那么这个三角形的周长和面积分别是多少?
例2
如图,是一只圆柱形的封闭易拉罐,它的底面半径为4cm,高为15cm,问易拉罐内可放的搅拌棒(直线型)最长可以是多长?
例3:已知单位长度为“1”,画一条线段,使它的长为
.
例4:如图,在正方形ABCD中,E是BC的中点,F为CD上一点,且
.试说明△AEF是直角三角形.
例5
如图,在四边形ABCD中,∠C=90°,AB=13,BC=4,CD=3,AD=12,试说明:AD⊥BD.
例6
已知:如图△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.求:BD的长.
例7:一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所爬行的最短路线的长是多少?
练习与测试
1.在Rt△ABC中,∠C=
,
(1)若
,则
;
(2)若
则
=
;
(3)
,则
2.以下各组数为三角形的三边,则不是直角三角形的是(
)
(A)13、12、5
(B)25、24、8
(C)
、2、
(D)
、
、7
3.一直角三角形的斜边比一直角边大4,另一直角边长为8,则斜边长为(
)
(A)6
(B)8
(C)10
(D)12
3.一直角三角形的斜边比一直角边大4,另一直角边长为8,则斜边长为(
)
(A)6
(B)8
(C)10
(D)12
4.已知在△ABC中,AB=AC,AD⊥BC于D,则下列正确的是(
)
(A)BC(B)∠B+∠CAD
=900
(C)AD>BD
(D)∠B>∠BAD
5.在等腰直角三角形中,斜边长为50cm,则它的面积为多少?
6.一架2.5米长的梯子靠在一座建筑物上,梯子的底部离建筑物0.7米,如果梯子的顶部滑下0.4米,梯子的底部向外滑出多远?
四、作业:课本P62
A、B组题
勾股定理的复习课(1)
一、复习与回顾
1、知识结构
2、勾股定理及其逆定理的作用
(1)勾股定理揭示了直角三角形边与边之间的数量关系,是解决有关线段计算问题的重要依据.
勾股定理的直接作用是知道直角三角形任意两边的长度,求第三边的长.这里一定要注意找准斜边、直角边;二要熟悉公式的变形:
(2)“若三角形的两条边的平方和等于第三边的平方,则这个三角形为
直角三角形”这一定理是勾股定理的逆定理.它可以帮助我们判断三角形的形状.为根据边的关系解决角的有关问题提供了新的方法.
勾股定理的作用:
①已知直角三角形的两边,求第三边;
②在数轴上作出表示(n为正整数)的点.
3、勾股定理及其逆定理的区别
勾股定理的逆定理是用来判定一个三角形是否是直角三角形的,但在判定一个三角形是否是直角三角形时应首先确定该三角形的最大边,当其余两边的平方和等于最大边的平方时,该三角形才是直角三角形.勾股定理的逆定理也可用来证明两直线是否垂直。
勾股定理是直角三角形的性质定理,而勾股定理的逆定理是直角三角形的判定定理,它不仅可以判定三角形是否为直角三角形,还可以判定哪一个角是直角,从而产生了证明两直线互相垂直的新方法:利用勾股定理的逆定理,通过计算来证明,体现了数形结合的思想.
4、知识的扩展
三角形的三边分别为a、b、c,其中c为最大边,若
,则三角形是直角三角形;
若
,则三角形是锐角三角形;
若
,则三角形是钝角三角形.所以使用勾股定理的逆定理时首先要确定三角形的最大边.
二、典型例题讲解
例1:如果一个直角三角形的两条边长分别是6cm和8cm,那么这个三角形的周长和面积分别是多少?
例2
如图,是一只圆柱形的封闭易拉罐,它的底面半径为4cm,高为15cm,问易拉罐内可放的搅拌棒(直线型)最长可以是多长?
例3:已知单位长度为“1”,画一条线段,使它的长为
.
例4:如图,在正方形ABCD中,E是BC的中点,F为CD上一点,且
.试说明△AEF是直角三角形.
例5
如图,在四边形ABCD中,∠C=90°,AB=13,BC=4,CD=3,AD=12,试说明:AD⊥BD.
例6
已知:如图△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.求:BD的长.
例7:一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所爬行的最短路线的长是多少?
练习与测试
1.在Rt△ABC中,∠C=
,
(1)若
,则
;
(2)若
则
=
;
(3)
,则
2.以下各组数为三角形的三边,则不是直角三角形的是(
)
(A)13、12、5
(B)25、24、8
(C)
、2、
(D)
、
、7
3.一直角三角形的斜边比一直角边大4,另一直角边长为8,则斜边长为(
)
(A)6
(B)8
(C)10
(D)12
3.一直角三角形的斜边比一直角边大4,另一直角边长为8,则斜边长为(
)
(A)6
(B)8
(C)10
(D)12
4.已知在△ABC中,AB=AC,AD⊥BC于D,则下列正确的是(
)
(A)BC
=900
(C)AD>BD
(D)∠B>∠BAD
5.在等腰直角三角形中,斜边长为50cm,则它的面积为多少?
6.一架2.5米长的梯子靠在一座建筑物上,梯子的底部离建筑物0.7米,如果梯子的顶部滑下0.4米,梯子的底部向外滑出多远?
四、作业:课本P62
A、B组题
