2020-2021学年人教版八年级下册:19.2.3一次函数与一次方程、不等式课件(15张ppt)
文档属性
| 名称 | 2020-2021学年人教版八年级下册:19.2.3一次函数与一次方程、不等式课件(15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 222.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 07:55:10 | ||
图片预览



文档简介
(共15张PPT)
一次函数与一元一次方程、不等式
1.
一次函数与一元一次方程
将一次函数y=kx+b中的y值看作0,则kx+b=0即为一元一次方程,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值,从图像上看,相当于求已知直线y=kx+b与x轴的交点的横坐标的值。
一.
知识要点:
2.
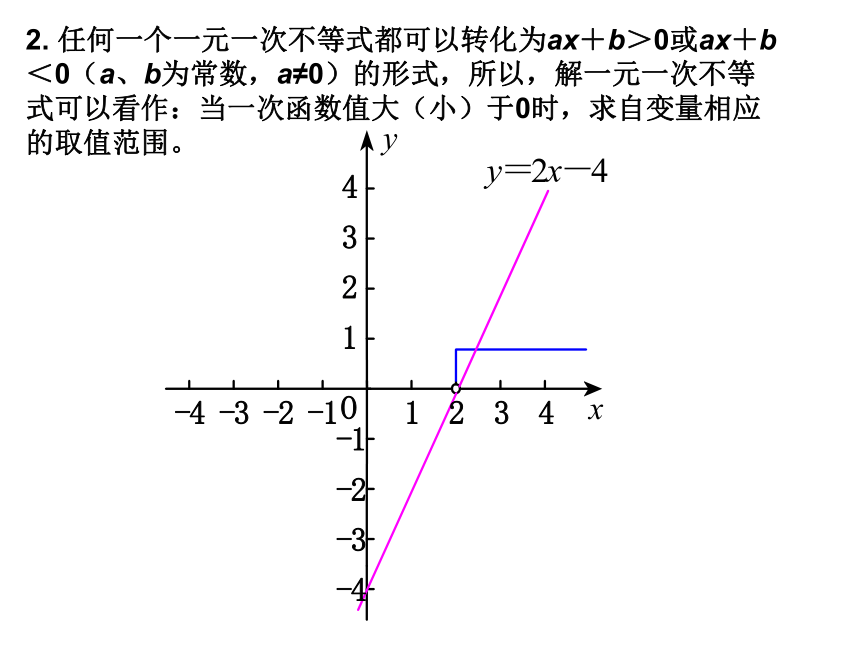
任何一个一元一次不等式都可以转化为ax+b>0或ax+b<0(a、b为常数,a≠0)的形式,所以,解一元一次不等式可以看作:当一次函数值大(小)于0时,求自变量相应的取值范围。
3.
二元一次方程与一次函数
由于任意一个二元一次方程都可以转化为y=kx+b的形式,所以每个二元一次方程都对应一个一次函数,于是也对应一条直线。
例如,二元一次方程2x-3y-6=0可以化为y=x-2,所以方程2x-3y-6=0对应直线y=x-2。
4.
二元一次方程组与一次函数
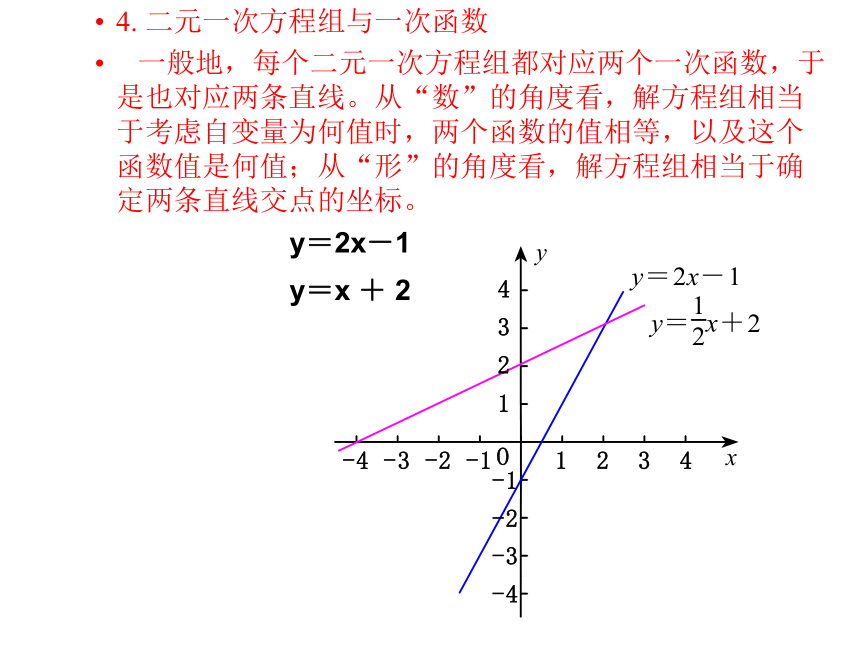
一般地,每个二元一次方程组都对应两个一次函数,于是也对应两条直线。从“数”的角度看,解方程组相当于考虑自变量为何值时,两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线交点的坐标。
y=2x-1
y=x
+
2
例1.
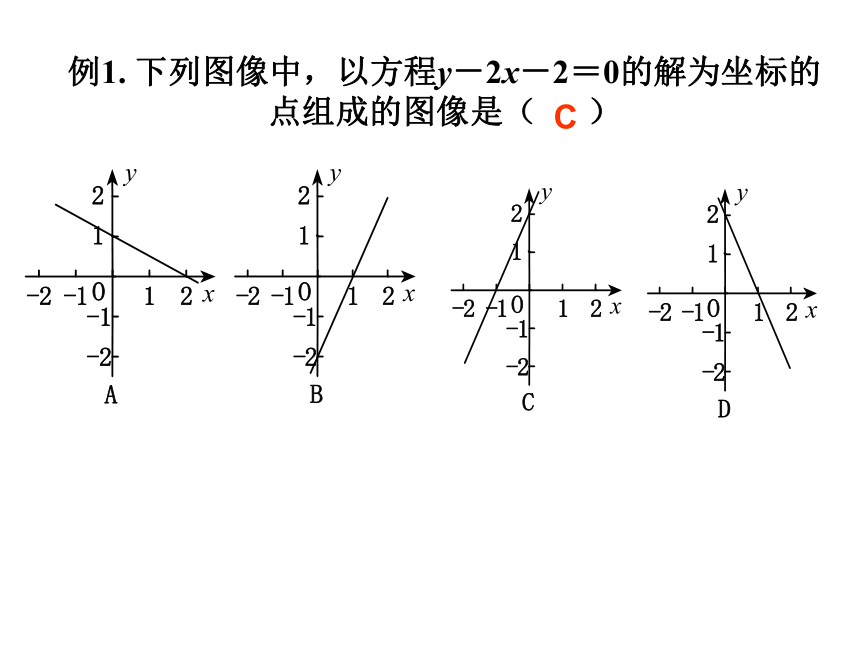
下列图像中,以方程y-2x-2=0的解为坐标的点组成的图像是(
)
C
例2.
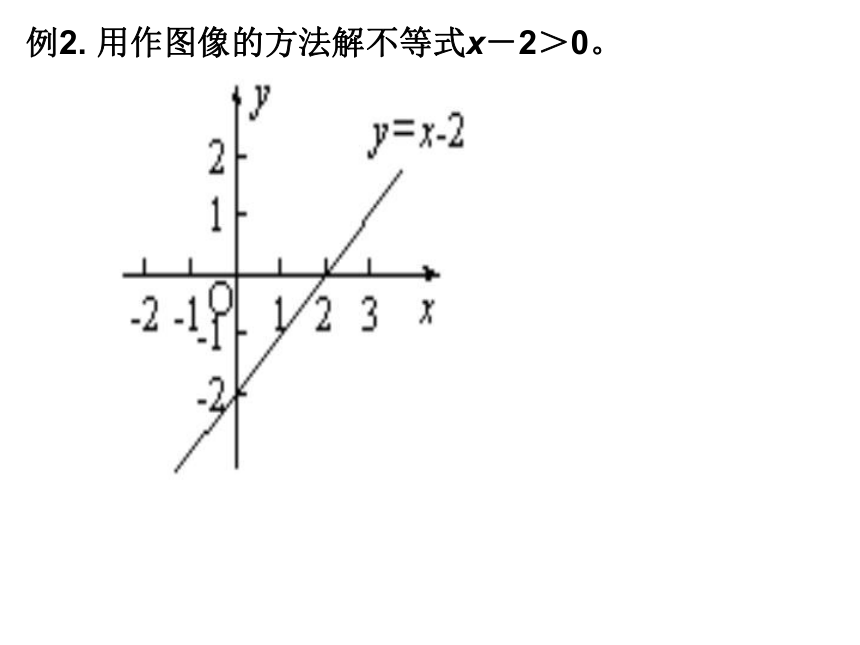
用作图像的方法解不等式x-2>0。
例3.
如图所示,已知函数y=ax+b和y=kx的图像交于点P,则根据图像可得,关于的二元一次方程组的解是__________。
解:
{
X=-4
y=-2
例4.
用作图像的方法解方程组。
分析:先把两个方程化成一次函数的形式,再在同一直角坐标系中画出它们的图像,交点的坐标就是方程组的解。
{
2x+y=4
2x-3y=12
y=-2
x=3
例5.
如图,直线L1的解析表达式为y=-3x+3,且L1与x轴交于点D。直线L2经过点A、B,并且
直线L1、L2交于点C。
(1)求点D的坐标;
(2)求直线L2的解析表达式和点C的坐标;
(3)求△ADC的面积;
(4)在直线L2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标。
答:(1)D(1,
0)
(2)y=3/2x-6
C(2,-,3)
(3)S△ADC=9/2
(4)P(6,3)
1.
点P1(x1,y1),点P2(x2,y2)是一次函数y=-4x+3图像上的两个点,且x1<x2,则y1与y2的大小关系是(
)
A.
y1>y2
B.
y1>y2>0
C.
y1<y2
D.
y1=y2
2.
直线L1:y=k1x+b与直线L2:y=k2x在同一平面直角坐标系中的图像如图所示,则关于x的不等式k1x+b>k2x的解为(
)
x>-1
B.
x<-1
C.
x<-2
D.
无法确定
A
B
练习
3.
如图所示,直线y=kx+b与x轴交于点(-4,0),当y>0时,x的取值范围是(
)
4.
已知一次函数y=kx+b的图像,如图所示,当x<0时,y的取值范围是(
)
A.
y>0
B.
y<0
C.
-2<y<0
D.
y<-2
A.
x>-4
B.
x>0
C.
x<-4
D.
x<0
A
D
5.
一次函数y=kx+b(k、b是常数,k≠0)的图像如图所示,则不等式kx+b>0的解集是(
)
x>-2
B.
x>0
C.
x<-2
D.
x<0
6.
一次函数y=kx+b的图像如图所示,当y<0时,x的取值范围是(
)
A.
x>0
B.
x<0
C.
x>2
D.
x<2
A
C
7.
一次函数y=(m-2)x+m的图像不经过第三象限,且m为正整数,则它的图像上纵坐标为-5的点的横坐标为__________。
8.莉莉有10元钱,她购买作业本后剩下的钱y(元)与购买的作业本数x满足函数y=10-1.2x,当剩下的钱y不超过2.8元时,她购买的作业本数x应满足____
_
_
__
_
_
6
6≤x≤8且x为整数
谢谢!
一次函数与一元一次方程、不等式
1.
一次函数与一元一次方程
将一次函数y=kx+b中的y值看作0,则kx+b=0即为一元一次方程,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值,从图像上看,相当于求已知直线y=kx+b与x轴的交点的横坐标的值。
一.
知识要点:
2.
任何一个一元一次不等式都可以转化为ax+b>0或ax+b<0(a、b为常数,a≠0)的形式,所以,解一元一次不等式可以看作:当一次函数值大(小)于0时,求自变量相应的取值范围。
3.
二元一次方程与一次函数
由于任意一个二元一次方程都可以转化为y=kx+b的形式,所以每个二元一次方程都对应一个一次函数,于是也对应一条直线。
例如,二元一次方程2x-3y-6=0可以化为y=x-2,所以方程2x-3y-6=0对应直线y=x-2。
4.
二元一次方程组与一次函数
一般地,每个二元一次方程组都对应两个一次函数,于是也对应两条直线。从“数”的角度看,解方程组相当于考虑自变量为何值时,两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线交点的坐标。
y=2x-1
y=x
+
2
例1.
下列图像中,以方程y-2x-2=0的解为坐标的点组成的图像是(
)
C
例2.
用作图像的方法解不等式x-2>0。
例3.
如图所示,已知函数y=ax+b和y=kx的图像交于点P,则根据图像可得,关于的二元一次方程组的解是__________。
解:
{
X=-4
y=-2
例4.
用作图像的方法解方程组。
分析:先把两个方程化成一次函数的形式,再在同一直角坐标系中画出它们的图像,交点的坐标就是方程组的解。
{
2x+y=4
2x-3y=12
y=-2
x=3
例5.
如图,直线L1的解析表达式为y=-3x+3,且L1与x轴交于点D。直线L2经过点A、B,并且
直线L1、L2交于点C。
(1)求点D的坐标;
(2)求直线L2的解析表达式和点C的坐标;
(3)求△ADC的面积;
(4)在直线L2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标。
答:(1)D(1,
0)
(2)y=3/2x-6
C(2,-,3)
(3)S△ADC=9/2
(4)P(6,3)
1.
点P1(x1,y1),点P2(x2,y2)是一次函数y=-4x+3图像上的两个点,且x1<x2,则y1与y2的大小关系是(
)
A.
y1>y2
B.
y1>y2>0
C.
y1<y2
D.
y1=y2
2.
直线L1:y=k1x+b与直线L2:y=k2x在同一平面直角坐标系中的图像如图所示,则关于x的不等式k1x+b>k2x的解为(
)
x>-1
B.
x<-1
C.
x<-2
D.
无法确定
A
B
练习
3.
如图所示,直线y=kx+b与x轴交于点(-4,0),当y>0时,x的取值范围是(
)
4.
已知一次函数y=kx+b的图像,如图所示,当x<0时,y的取值范围是(
)
A.
y>0
B.
y<0
C.
-2<y<0
D.
y<-2
A.
x>-4
B.
x>0
C.
x<-4
D.
x<0
A
D
5.
一次函数y=kx+b(k、b是常数,k≠0)的图像如图所示,则不等式kx+b>0的解集是(
)
x>-2
B.
x>0
C.
x<-2
D.
x<0
6.
一次函数y=kx+b的图像如图所示,当y<0时,x的取值范围是(
)
A.
x>0
B.
x<0
C.
x>2
D.
x<2
A
C
7.
一次函数y=(m-2)x+m的图像不经过第三象限,且m为正整数,则它的图像上纵坐标为-5的点的横坐标为__________。
8.莉莉有10元钱,她购买作业本后剩下的钱y(元)与购买的作业本数x满足函数y=10-1.2x,当剩下的钱y不超过2.8元时,她购买的作业本数x应满足____
_
_
__
_
_
6
6≤x≤8且x为整数
谢谢!
