2020--2021学年北师大版八年级数学下册第三章图形的平移和旋转---中心对称课件(共26张PPT)
文档属性
| 名称 | 2020--2021学年北师大版八年级数学下册第三章图形的平移和旋转---中心对称课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 758.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 16:53:18 | ||
图片预览




文档简介
(共26张PPT)
北师大版
八年级下册
3.3
中心对称
第三章
图平移与旋转
1.
下面哪些图形是中心对称图形?
(1)
、(2)
、(3)
一、预习检测
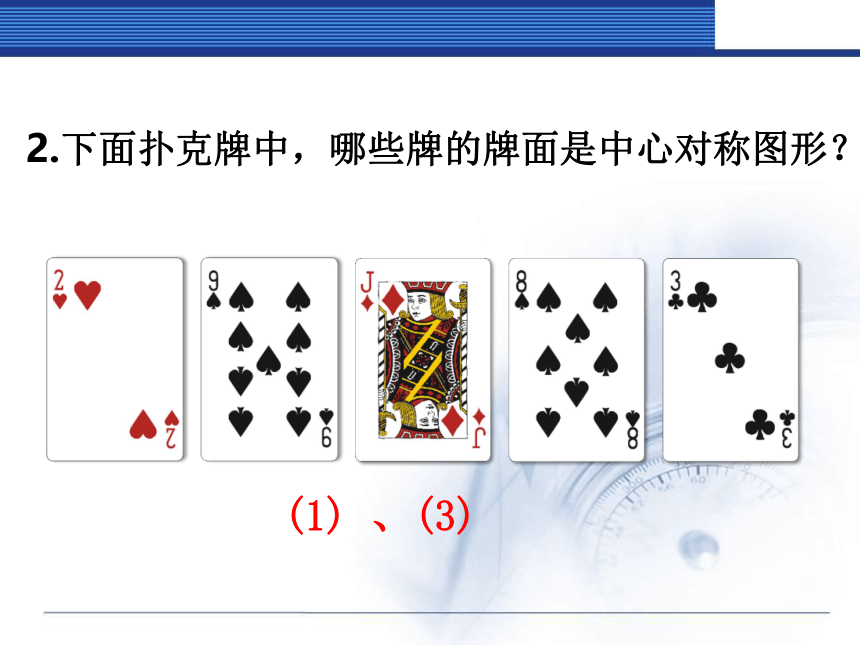
2.下面扑克牌中,哪些牌的牌面是中心对称图形?
(1)
、(3)
B
A
E
D
O
C
θ
F
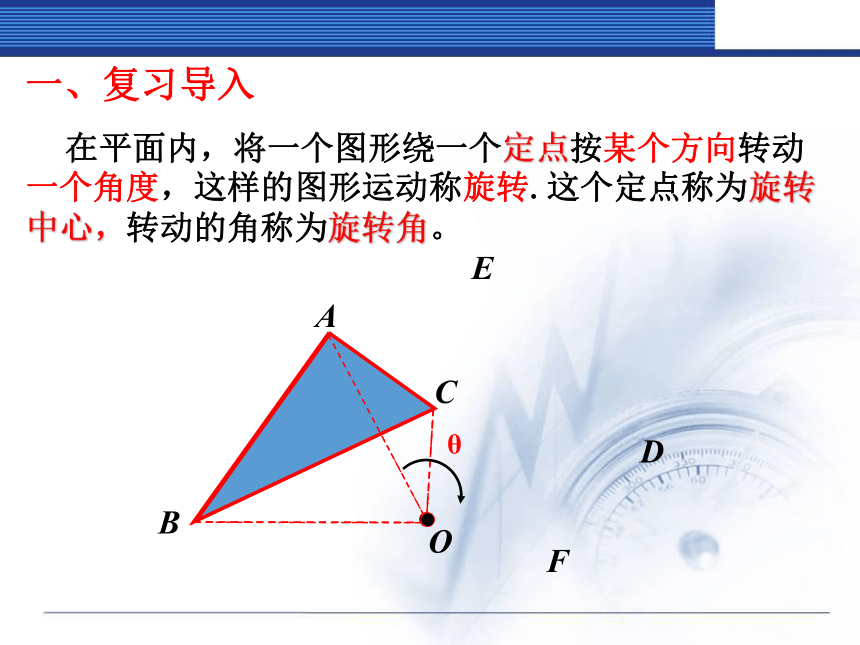
一、复习导入
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称旋转.这个定点称为旋转中心,转动的角称为旋转角。
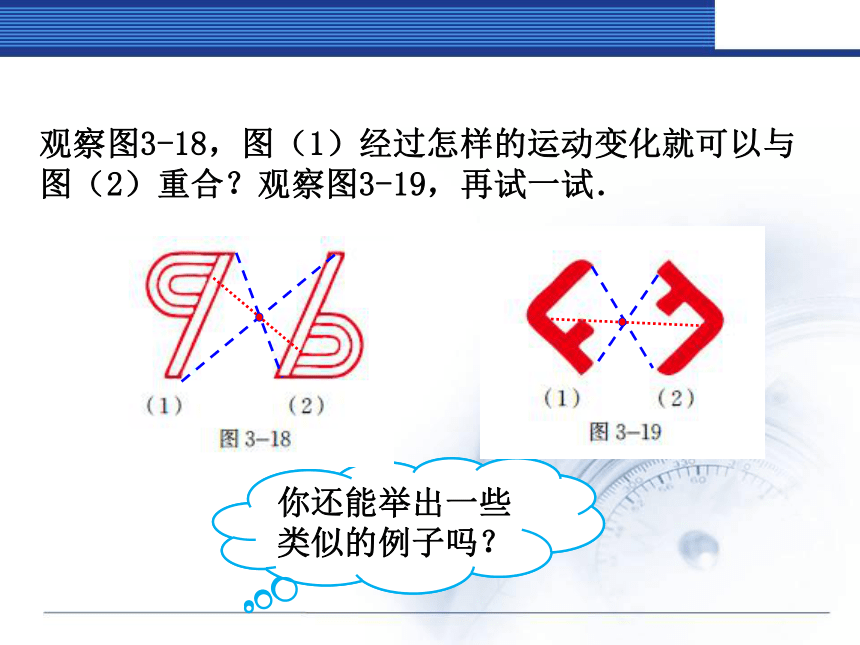
观察图3-18,图(1)经过怎样的运动变化就可以与图(2)重合?观察图3-19,再试一试.
你还能举出一些类似的例子吗?
B
A
E
D
O
C
F
二、探究新知
观察,两个三角形重合的运动过程
此运动和旋转有什么联系?
(一)
中心对称
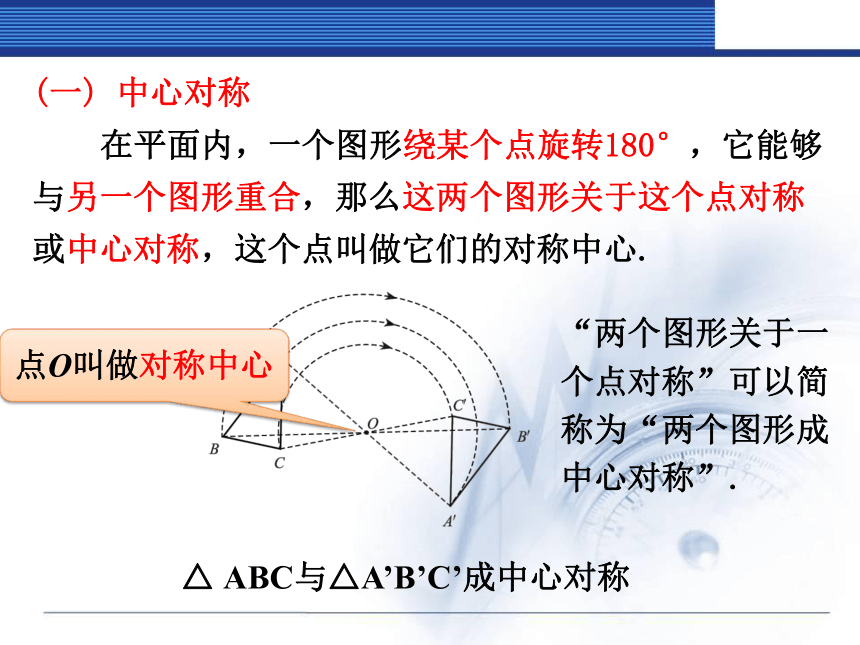
在平面内,一个图形绕某个点旋转180°,它能够与另一个图形重合,那么这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心.
“两个图形关于一个点对称”可以简称为“两个图形成中心对称”.
△
ABC与△A’B’C’成中心对称
点O叫做对称中心
1.中心对称是一种特殊的旋转.其旋转角是180
°.
2.中心对称是对两个图形来说的,它表示两个图形的一种特殊的位置关系.
归纳总结
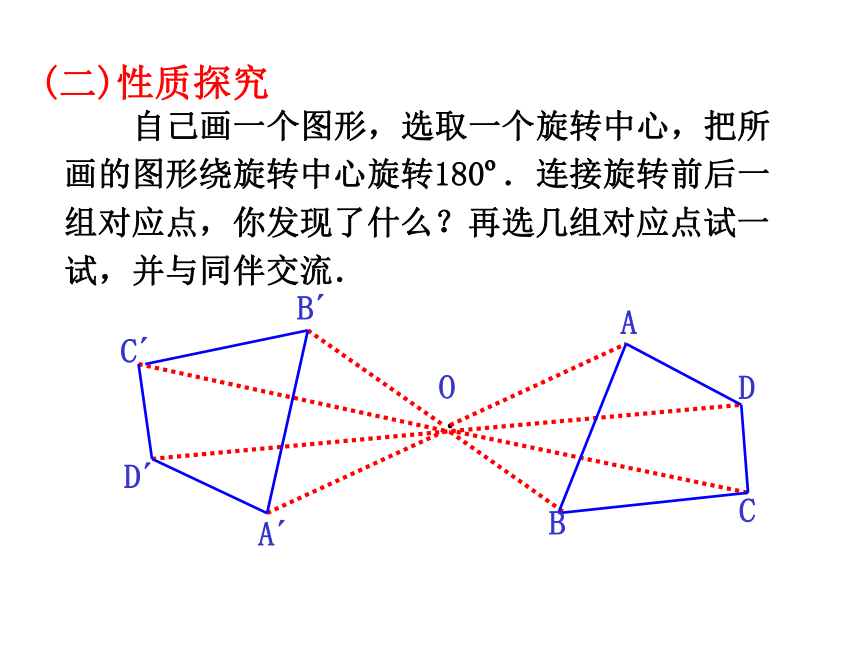
自己画一个图形,选取一个旋转中心,把所画的图形绕旋转中心旋转180?.连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试,并与同伴交流.
.
C?
D?
A
B
D
C
O
A?
B?
(二)性质探究
.
C?
D?
A
B
D
C
O
A?
B?
(2)关于中心对称的两个图形,对应点所连线
段都经过对称中心,且被对称中心平分.
(1)关于中心对称的两个图形是全等图形;
中心对称的性质:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
活动小结:
注意:连接任意两对对应点,两条线段的交点就是对称中心.
例1
在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1关于某一点中心对称,则对称中心的坐标为_________.?
方法点拨:
确定对称中心的两种方法
1.连接一对对称点,该线段的中点即为对称中心.
2.连接两对对称点,交点即为对称中心.
(2,1)
轴
对
称
中
心
对
称
有一条对称轴
—
直线
有一个对称中心
—
点
图形沿轴对折(翻转)
180°
图形绕对称中心旋转
180°
对称点的连线被对称轴垂直平分
中心对称与轴对称的联系与区别
A
B
C
C′
A′
B′
O
对应点所连线段经过对称中心,且被对称中心平分
例1:
如图,点O是线段AE的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形.
解:如图,连接BO并延长至B′,使OB′=OB;
连接CO并延长至C′,使OC′=OC;
连接DO并延长至D′,使OD′=OD;
顺次连接E,B′,C′,D′,A.
图形EB′C′D′A就是以点O为对称中心、与五边形ABCDE成中心对称的图形.
观察下图,这些图形有什么共同特征?你还能举出一些类似的图形吗?
三、知识探究二
共同点:
(1)都绕一点旋转了180度;
(2)都与原图形完全重合.
中心对称图形
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
注意:任意经过对称中心的直线把
原图形分成全等的两部分
中心对称与中心对称图形的联系
中心对称
中心对称图形
区别
联系
两个全等图形的相互位置关系
一个图形本身成中心对称
成中心对称的两个图形看成一个整体,则它们是中心对称图形.
中心对称图形对称的部分看成两个图形,则它们成中心对称.
我们平时见过的几何图形中,有哪些是中心对称图形?并指出对称中心.
怎样的多边形是中心对称图形?
偶数边的正多边形
想一想
1.下列多边形中,是中心对称图形而不是轴对称图形的是(
)
A.平行四边形
B.矩形
C.菱形
D.正方形
A
2.如下所示的4组图形中,左边数字与右边数字成中心对称的有(
)
A.1组
B.2组
C.3组
D.4组
四.课堂检测
C
3如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是(
)
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
D
4.在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
5.若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是(
)
A.1
B.3
C.5
D.7
C
例4
请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎样画?
割法1
割法2
补法
对于这种由两个中心对称图形组成的复合图形,平分面积时,关键找到它们的对称中心,再过对称中心作直线.
归纳
中心对称和
中心对称图形
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
中心对称图形
定义
性质
应用
绕着内部一点旋转180°能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
五、课堂小结
六、布置作业
必做题:绩优学案65
例3
选做题:基础层
绩优学案66
基础练
第2题
提升层
绩优学案66
基础练
第2,3题
北师大版
八年级下册
3.3
中心对称
第三章
图平移与旋转
1.
下面哪些图形是中心对称图形?
(1)
、(2)
、(3)
一、预习检测
2.下面扑克牌中,哪些牌的牌面是中心对称图形?
(1)
、(3)
B
A
E
D
O
C
θ
F
一、复习导入
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称旋转.这个定点称为旋转中心,转动的角称为旋转角。
观察图3-18,图(1)经过怎样的运动变化就可以与图(2)重合?观察图3-19,再试一试.
你还能举出一些类似的例子吗?
B
A
E
D
O
C
F
二、探究新知
观察,两个三角形重合的运动过程
此运动和旋转有什么联系?
(一)
中心对称
在平面内,一个图形绕某个点旋转180°,它能够与另一个图形重合,那么这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心.
“两个图形关于一个点对称”可以简称为“两个图形成中心对称”.
△
ABC与△A’B’C’成中心对称
点O叫做对称中心
1.中心对称是一种特殊的旋转.其旋转角是180
°.
2.中心对称是对两个图形来说的,它表示两个图形的一种特殊的位置关系.
归纳总结
自己画一个图形,选取一个旋转中心,把所画的图形绕旋转中心旋转180?.连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试,并与同伴交流.
.
C?
D?
A
B
D
C
O
A?
B?
(二)性质探究
.
C?
D?
A
B
D
C
O
A?
B?
(2)关于中心对称的两个图形,对应点所连线
段都经过对称中心,且被对称中心平分.
(1)关于中心对称的两个图形是全等图形;
中心对称的性质:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
活动小结:
注意:连接任意两对对应点,两条线段的交点就是对称中心.
例1
在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1关于某一点中心对称,则对称中心的坐标为_________.?
方法点拨:
确定对称中心的两种方法
1.连接一对对称点,该线段的中点即为对称中心.
2.连接两对对称点,交点即为对称中心.
(2,1)
轴
对
称
中
心
对
称
有一条对称轴
—
直线
有一个对称中心
—
点
图形沿轴对折(翻转)
180°
图形绕对称中心旋转
180°
对称点的连线被对称轴垂直平分
中心对称与轴对称的联系与区别
A
B
C
C′
A′
B′
O
对应点所连线段经过对称中心,且被对称中心平分
例1:
如图,点O是线段AE的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形.
解:如图,连接BO并延长至B′,使OB′=OB;
连接CO并延长至C′,使OC′=OC;
连接DO并延长至D′,使OD′=OD;
顺次连接E,B′,C′,D′,A.
图形EB′C′D′A就是以点O为对称中心、与五边形ABCDE成中心对称的图形.
观察下图,这些图形有什么共同特征?你还能举出一些类似的图形吗?
三、知识探究二
共同点:
(1)都绕一点旋转了180度;
(2)都与原图形完全重合.
中心对称图形
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
注意:任意经过对称中心的直线把
原图形分成全等的两部分
中心对称与中心对称图形的联系
中心对称
中心对称图形
区别
联系
两个全等图形的相互位置关系
一个图形本身成中心对称
成中心对称的两个图形看成一个整体,则它们是中心对称图形.
中心对称图形对称的部分看成两个图形,则它们成中心对称.
我们平时见过的几何图形中,有哪些是中心对称图形?并指出对称中心.
怎样的多边形是中心对称图形?
偶数边的正多边形
想一想
1.下列多边形中,是中心对称图形而不是轴对称图形的是(
)
A.平行四边形
B.矩形
C.菱形
D.正方形
A
2.如下所示的4组图形中,左边数字与右边数字成中心对称的有(
)
A.1组
B.2组
C.3组
D.4组
四.课堂检测
C
3如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是(
)
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
D
4.在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
5.若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是(
)
A.1
B.3
C.5
D.7
C
例4
请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎样画?
割法1
割法2
补法
对于这种由两个中心对称图形组成的复合图形,平分面积时,关键找到它们的对称中心,再过对称中心作直线.
归纳
中心对称和
中心对称图形
概念
旋转角是180°
性质
对应点的连线经过对称中心,且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
中心对称图形
定义
性质
应用
绕着内部一点旋转180°能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
五、课堂小结
六、布置作业
必做题:绩优学案65
例3
选做题:基础层
绩优学案66
基础练
第2题
提升层
绩优学案66
基础练
第2,3题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
