2020-2021学年人教版数学八年级下册18.1.1平行四边形的性质课件(共17张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册18.1.1平行四边形的性质课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 325.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 17:03:42 | ||
图片预览



文档简介
(共15张PPT)
八年级-下册-第18章节
课题:18.1平行四边形的定义及性质
难点: 平行四边形性质的应用
目录
CONTENTS
B
D
C
A
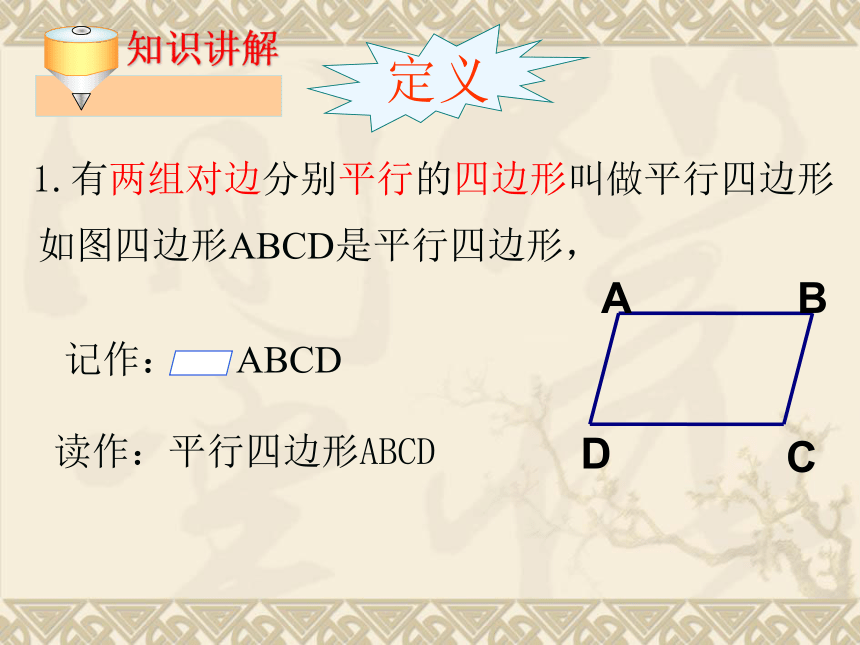
1.有两组对边分别平行的四边形叫做平行四边形
知识讲解
如图四边形ABCD是平行四边形,
记作: ABCD
定义
读作:平行四边形ABCD
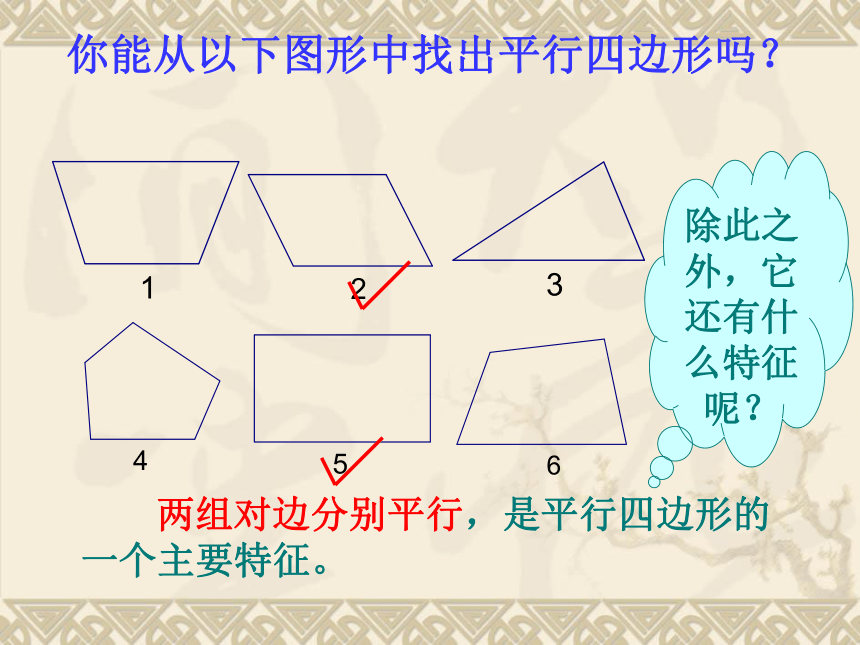
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
除此之外,它还有什么特征呢?
B
A
D
c
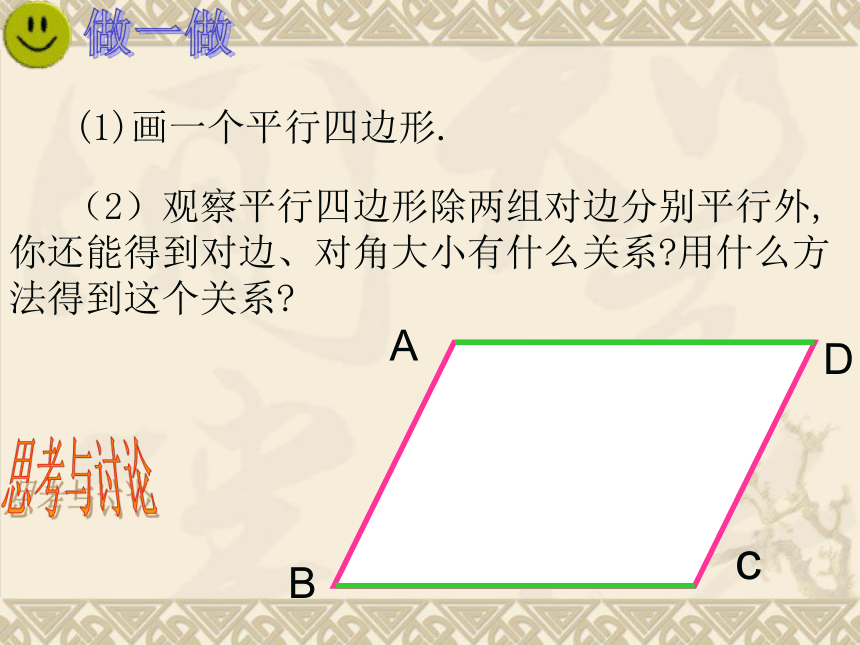
(2)观察平行四边形除两组对边分别平行外, 你还能得到对边、对角大小有什么关系 用什么方法得到这个关系
思考与讨论
(1)画一个平行四边形.
做一做
平行四边形的对边相等;
平行四边形的对角相等.
你能证明我们的猜想吗?
猜想
平行四边形对边、对角各有什么关系?
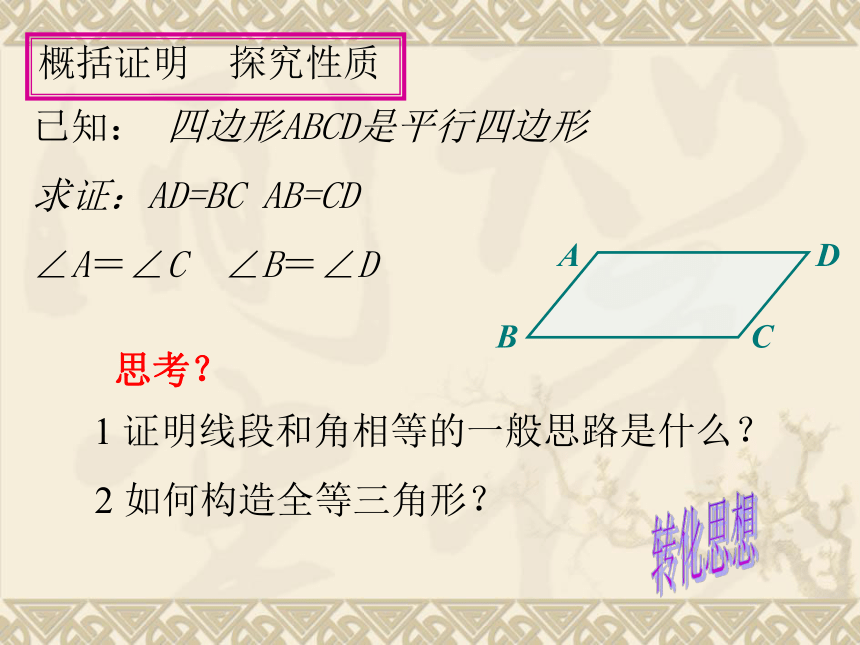
已知: 四边形ABCD是平行四边形
求证:AD=BC AB=CD
∠A=∠C ∠B=∠D
B
C
D
A
思考?
1 证明线段和角相等的一般思路是什么?
2 如何构造全等三角形?
概括证明 探究性质
转化思想
证明:如图,连接AC.
∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,
∴∠ 1 = , ∠3 = .
在△ABC和△CDA中
_____________
_____________(公共边)
_____________
∴△ABC ≌ ( ).
∴AB= ,AD= , ∠ B= .
∵∠1+∠4_____∠2+∠3
∴ ∠BAD= ∠BCD
∠2
∠4
∠1=∠2
AC=AC
∠3=∠4
△ADC
ASA
CD
BC
∠D
=
A
B
C
D
1
2
3
4
概括证明 探究性质
概括证明 探究性质
平行四边形的性质定理:
平行四边形的对边相等;
平行四边形的对角相等,邻角互补;
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC
∠A=∠C,∠B=∠D
几何语言
B
C
D
A
(1) 在□ABCD中,已知AB=5,BC=3,
求它的周长;
解:如图, 在平行四边形ABCD中,
∴ AB=CD=5,
BC=AD=3,
∴平行四边形的周长=2 x(AB+BC)
=2 x(5+3)
=16
D C
A B
小结:平行四边形的周长等于邻边和的二倍。
课堂练习
(2)在□ABCD中,已知∠A=38°,
求其余各内角的度数.
解:如图, ∵四边形ABCD为
平行四边形,
∴AB∥CD,
又∵ ∠A=38°
∴ ∠D=180 °- ∠A
=180°- 38°
=142°
又∵平行四边形的对角相等
∴ ∠C= ∠A=38°
∠B= ∠D= 142°
D C
A B
课堂练习
速算
1 、在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。
A
B
C
D
80°
100°
80°
100°
体会 分享 小结
能说出你这节课的收获和体验
让大家与你分享吗
1、平行四边形的定义、符号表示法;
2、平行四边形的性质
平行四边形的对边相等;
平行四边形的对角相等;邻角互补
3、平行四边形性质的应用
体会 分享 小结
作业布置
1、作业:
习题18.1 第1、2 、8题
2 、请同学们课下探讨:
平行四边形的对角线具有什么性质?
八年级-下册-第18章节
课题:18.1平行四边形的定义及性质
难点: 平行四边形性质的应用
目录
CONTENTS
B
D
C
A
1.有两组对边分别平行的四边形叫做平行四边形
知识讲解
如图四边形ABCD是平行四边形,
记作: ABCD
定义
读作:平行四边形ABCD
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
除此之外,它还有什么特征呢?
B
A
D
c
(2)观察平行四边形除两组对边分别平行外, 你还能得到对边、对角大小有什么关系 用什么方法得到这个关系
思考与讨论
(1)画一个平行四边形.
做一做
平行四边形的对边相等;
平行四边形的对角相等.
你能证明我们的猜想吗?
猜想
平行四边形对边、对角各有什么关系?
已知: 四边形ABCD是平行四边形
求证:AD=BC AB=CD
∠A=∠C ∠B=∠D
B
C
D
A
思考?
1 证明线段和角相等的一般思路是什么?
2 如何构造全等三角形?
概括证明 探究性质
转化思想
证明:如图,连接AC.
∵四边形ABCD为平行四边形,
∴AD∥BC,AB∥CD,
∴∠ 1 = , ∠3 = .
在△ABC和△CDA中
_____________
_____________(公共边)
_____________
∴△ABC ≌ ( ).
∴AB= ,AD= , ∠ B= .
∵∠1+∠4_____∠2+∠3
∴ ∠BAD= ∠BCD
∠2
∠4
∠1=∠2
AC=AC
∠3=∠4
△ADC
ASA
CD
BC
∠D
=
A
B
C
D
1
2
3
4
概括证明 探究性质
概括证明 探究性质
平行四边形的性质定理:
平行四边形的对边相等;
平行四边形的对角相等,邻角互补;
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC
∠A=∠C,∠B=∠D
几何语言
B
C
D
A
(1) 在□ABCD中,已知AB=5,BC=3,
求它的周长;
解:如图, 在平行四边形ABCD中,
∴ AB=CD=5,
BC=AD=3,
∴平行四边形的周长=2 x(AB+BC)
=2 x(5+3)
=16
D C
A B
小结:平行四边形的周长等于邻边和的二倍。
课堂练习
(2)在□ABCD中,已知∠A=38°,
求其余各内角的度数.
解:如图, ∵四边形ABCD为
平行四边形,
∴AB∥CD,
又∵ ∠A=38°
∴ ∠D=180 °- ∠A
=180°- 38°
=142°
又∵平行四边形的对角相等
∴ ∠C= ∠A=38°
∠B= ∠D= 142°
D C
A B
课堂练习
速算
1 、在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。
A
B
C
D
80°
100°
80°
100°
体会 分享 小结
能说出你这节课的收获和体验
让大家与你分享吗
1、平行四边形的定义、符号表示法;
2、平行四边形的性质
平行四边形的对边相等;
平行四边形的对角相等;邻角互补
3、平行四边形性质的应用
体会 分享 小结
作业布置
1、作业:
习题18.1 第1、2 、8题
2 、请同学们课下探讨:
平行四边形的对角线具有什么性质?
