2020-2021学年高一数学北师大版必修5单元自我测试卷 第二章 解三角形 B卷 Word版含解析
文档属性
| 名称 | 2020-2021学年高一数学北师大版必修5单元自我测试卷 第二章 解三角形 B卷 Word版含解析 |
|
|
| 格式 | doc | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 14:41:06 | ||
图片预览



文档简介
2020-2021学年高一数学北师大版必修5
第二章 解三角形 B卷
1.如图所示,在地面上共线的三点处测得一建筑物的仰角分别为,且,则建筑物的高度为( )
A. B. C. D.
2.如图,两座相距的建筑物的高度分别为为水平线,则从建筑物AB的顶端A看建筑物CD的视角的大小是( )
A. B. C. D.
3.如图,要测出山上石油钻井的井架BC的高,从山脚A测得,塔顶B的仰角为,塔底C的仰角为,则井架BC的高为( )
A. B. C. D.
4.如图,两点在河的两岸,在A所在的河岸边选一定点C,测量AC的距离为,则两点间的距离是( )
A. B. C. D.
5.一艘轮船以18海里/时的速度沿北偏东的方向直线航行,在行驶到某处时,该轮船南偏东方向上10海里处有一灯塔,继续行驶20分钟后,轮船与灯塔的距离为( )
A.17海里 B.16海里 C.15海里 D.14海里
6.在中,若,则一定是( )。
A.直角三角形 B.等腰直角三角形 C.正三角形 D.等腰三角形
7.在中,角所对的边分别为,若,则为( )。
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
8.在中,,则是( )。
A.等边三角形 B.等腰三角形 C.直角三角形 D.锐角三角形
9.在相距2的两点处测量目标,若,则、
两点之间的距离是( )
A. B.
C. D.3
10.如图,测量员在水平线上点B处测得一塔的塔顶仰角为,当他前进到达点C处时,测得塔顶仰角为,则塔高为( )
A. B. C. D.
11.在中,内角所对的边分别为.若,则______.
12.在不等边三角形中,为最大边,若,则A的取值范围为_________.
13.在中,已知,且,角是锐角,则的形状是__________.
14.如图6-6所示,为测量山高,选择和另一座山的山顶为测量观测点。从点测得点的仰角点的仰角以及。从点测得,已知山高,则山高___________。
15.在中,内角的对边分别为,已知向量,且.
(1)求角A的大小;
(2)若,求面积的最大值.
答案以及解析
1.答案:D
解析:设建筑物的高度为.由题图知,.在和中,分别由余弦定理得,,①.②.③由①②③,解得或(舍去).即建筑物的高度为.
2.答案:B
解析:.在中,由余弦定理得,故.故选B.
3.答案:B
解析:由题意得在中,,且,由正弦定理得,即,解得.
4.答案:A
解析:在中,,所以,由正弦定理得,所以.故选A.
5.答案:D
解析:记轮船行驶到某处的位置为A,灯塔的位置为B,20分钟后轮船的位置为C,如图所示则,所以,所以.故20分钟后,轮船与灯塔的距离为14海里.故选D.
6.答案:D
解析:,由向量加法的平行四边形法则知,以为邻边的平行四边形的对角线互相垂直,所以一定是等腰三角形。
7.答案:A
解析:依题意得,即,
所以。
即。
所以。
又,于是有,所以为钝角,
所以是钝角三角形。
8.答案:C
解析: 由正弦定理可得是直角三角形。
9.答案:A
解析:∵,
∴,
由正弦定理,即,
解得:.
10.答案:C
解析:设塔高为,则,.
因为,所以,所以.
故选C.
11.答案:
解析:因为,所以,所以由正弦定理得.
12.答案:
解析:,,则.
.又为最大边,.
故A的取值范围是.
13.答案:等边三角形
解析:.
由正弦定理得:,
即,,角是锐角,则.
,则,故的形状是等边三角形.
14.答案:150
解析:在中,,在中,,解得,在中,,故,即山高为。
15.答案:(1)因为,
所以,
即,
即,即.
因为,所以,
所以,所以.
(2)由余弦定理可得,,
当且仅当时取等号,所以,
所以,
即面积的最大值为.
第二章 解三角形 B卷
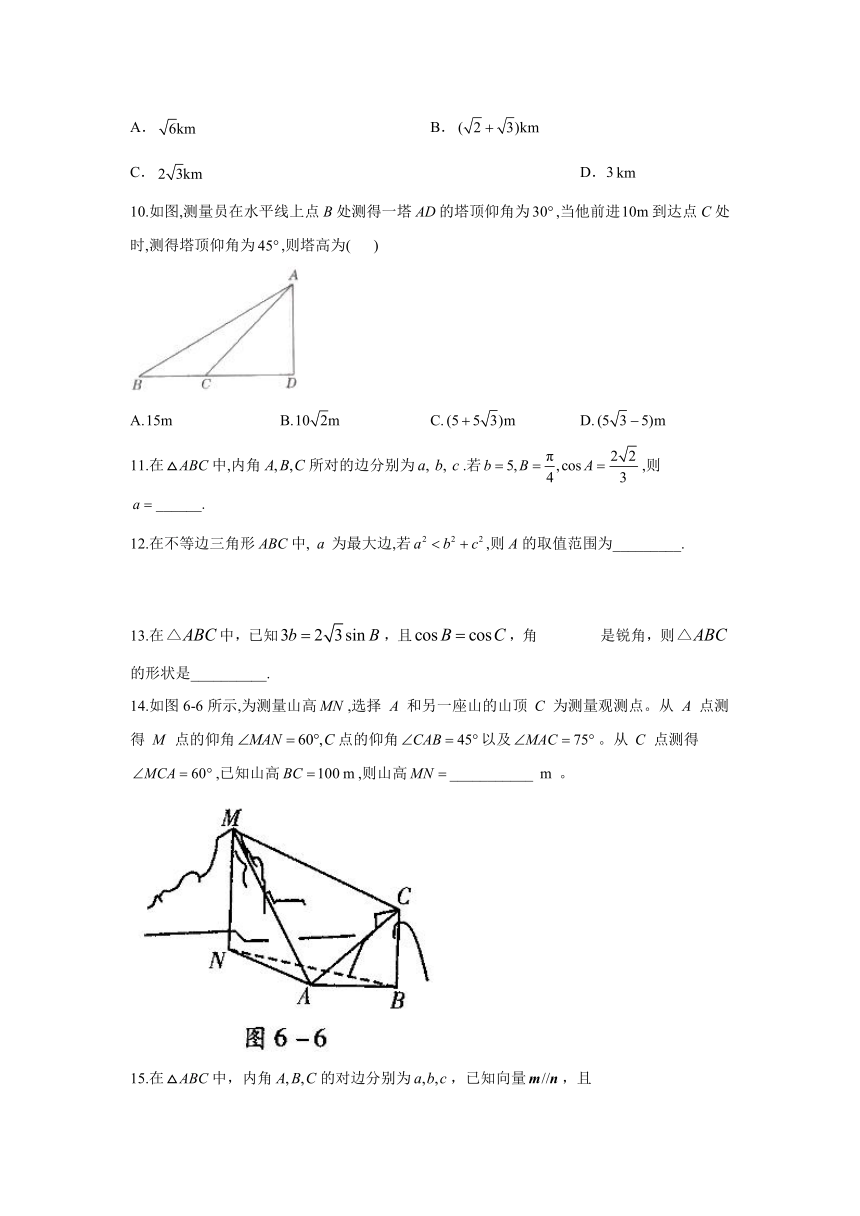
1.如图所示,在地面上共线的三点处测得一建筑物的仰角分别为,且,则建筑物的高度为( )
A. B. C. D.
2.如图,两座相距的建筑物的高度分别为为水平线,则从建筑物AB的顶端A看建筑物CD的视角的大小是( )
A. B. C. D.
3.如图,要测出山上石油钻井的井架BC的高,从山脚A测得,塔顶B的仰角为,塔底C的仰角为,则井架BC的高为( )
A. B. C. D.
4.如图,两点在河的两岸,在A所在的河岸边选一定点C,测量AC的距离为,则两点间的距离是( )
A. B. C. D.
5.一艘轮船以18海里/时的速度沿北偏东的方向直线航行,在行驶到某处时,该轮船南偏东方向上10海里处有一灯塔,继续行驶20分钟后,轮船与灯塔的距离为( )
A.17海里 B.16海里 C.15海里 D.14海里
6.在中,若,则一定是( )。
A.直角三角形 B.等腰直角三角形 C.正三角形 D.等腰三角形
7.在中,角所对的边分别为,若,则为( )。
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
8.在中,,则是( )。
A.等边三角形 B.等腰三角形 C.直角三角形 D.锐角三角形
9.在相距2的两点处测量目标,若,则、
两点之间的距离是( )
A. B.
C. D.3
10.如图,测量员在水平线上点B处测得一塔的塔顶仰角为,当他前进到达点C处时,测得塔顶仰角为,则塔高为( )
A. B. C. D.
11.在中,内角所对的边分别为.若,则______.
12.在不等边三角形中,为最大边,若,则A的取值范围为_________.
13.在中,已知,且,角是锐角,则的形状是__________.
14.如图6-6所示,为测量山高,选择和另一座山的山顶为测量观测点。从点测得点的仰角点的仰角以及。从点测得,已知山高,则山高___________。
15.在中,内角的对边分别为,已知向量,且.
(1)求角A的大小;
(2)若,求面积的最大值.
答案以及解析
1.答案:D
解析:设建筑物的高度为.由题图知,.在和中,分别由余弦定理得,,①.②.③由①②③,解得或(舍去).即建筑物的高度为.
2.答案:B
解析:.在中,由余弦定理得,故.故选B.
3.答案:B
解析:由题意得在中,,且,由正弦定理得,即,解得.
4.答案:A
解析:在中,,所以,由正弦定理得,所以.故选A.
5.答案:D
解析:记轮船行驶到某处的位置为A,灯塔的位置为B,20分钟后轮船的位置为C,如图所示则,所以,所以.故20分钟后,轮船与灯塔的距离为14海里.故选D.
6.答案:D
解析:,由向量加法的平行四边形法则知,以为邻边的平行四边形的对角线互相垂直,所以一定是等腰三角形。
7.答案:A
解析:依题意得,即,
所以。
即。
所以。
又,于是有,所以为钝角,
所以是钝角三角形。
8.答案:C
解析: 由正弦定理可得是直角三角形。
9.答案:A
解析:∵,
∴,
由正弦定理,即,
解得:.
10.答案:C
解析:设塔高为,则,.
因为,所以,所以.
故选C.
11.答案:
解析:因为,所以,所以由正弦定理得.
12.答案:
解析:,,则.
.又为最大边,.
故A的取值范围是.
13.答案:等边三角形
解析:.
由正弦定理得:,
即,,角是锐角,则.
,则,故的形状是等边三角形.
14.答案:150
解析:在中,,在中,,解得,在中,,故,即山高为。
15.答案:(1)因为,
所以,
即,
即,即.
因为,所以,
所以,所以.
(2)由余弦定理可得,,
当且仅当时取等号,所以,
所以,
即面积的最大值为.
