2020--2021学年北师大版数学七年级下册4.3:利用“角边角”“角角边”判定三角形全等试卷(Word版含答案)
文档属性
| 名称 | 2020--2021学年北师大版数学七年级下册4.3:利用“角边角”“角角边”判定三角形全等试卷(Word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 126.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 00:00:00 | ||
图片预览



文档简介
[利用“角边角”“角角边”判定三角形全等]
一、选择题
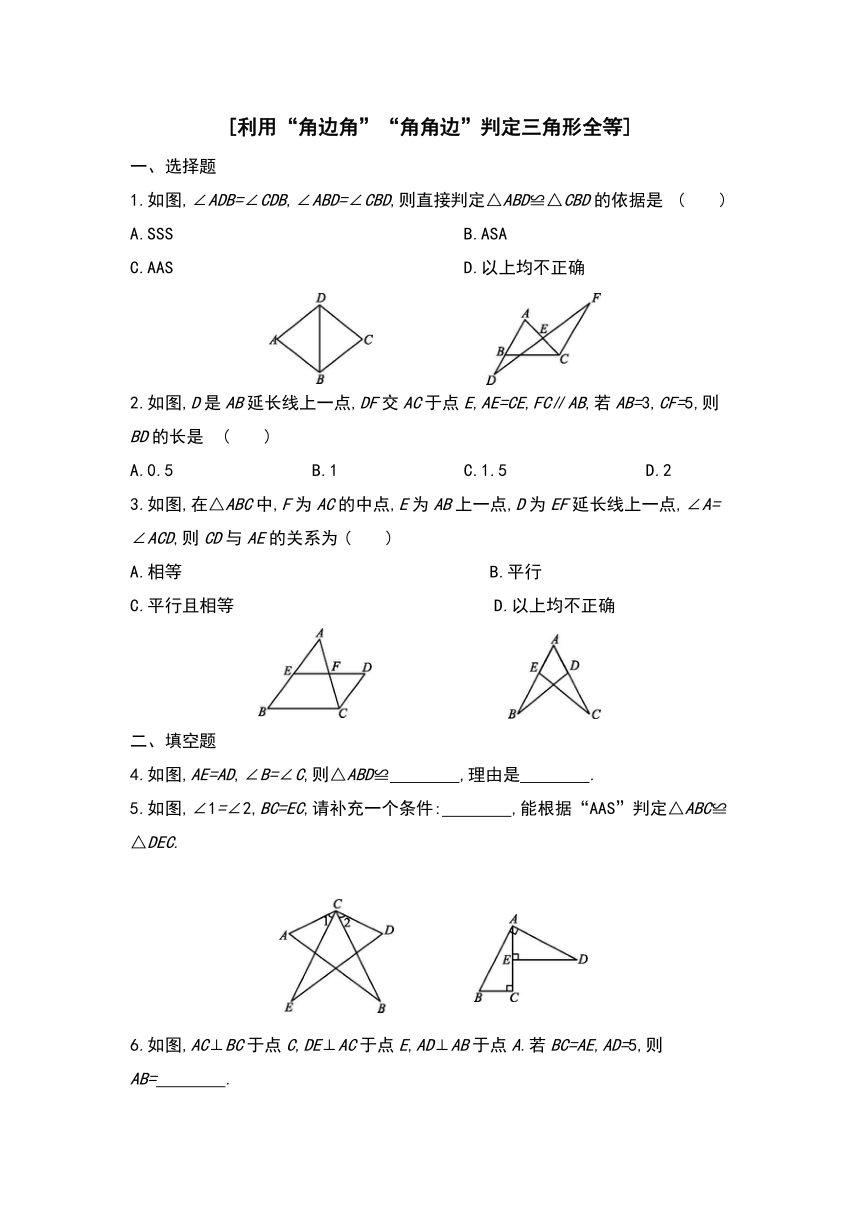
1.如图,∠ADB=∠CDB,∠ABD=∠CBD,则直接判定△ABD≌△CBD的依据是
( )
A.SSS
B.ASA
C.AAS
D.以上均不正确
2.如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是
( )
A.0.5
B.1
C.1.5
D.2
3.如图,在△ABC中,F为AC的中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为
( )
A.相等
B.平行
C.平行且相等
D.以上均不正确
二、填空题
4.如图,AE=AD,∠B=∠C,则△ABD≌ ,理由是 .?
5.如图,∠1=∠2,BC=EC,请补充一个条件: ,能根据“AAS”判定△ABC≌△DEC.?
6.如图,AC⊥BC于点C,DE⊥AC于点E,AD⊥AB于点A.若BC=AE,AD=5,则AB= .?
7.如图,AB∥CD,AB=CD,AD∥BC,AD=BC,BD,AC交于点O,EF是过点O的线段,分别交AD,BC于点E,F,则图中的全等三角形有 对.?
8.如图,已知∠CAB=∠DBA,∠CBD=∠DAC,请将下面说明AD=BC的过程和理由补充完整.
解:因为∠DBA=∠CAB,∠CBD=∠DAC,
所以∠CBD+∠DBA=∠DAC+∠CAB,
所以∠CBA=∠DAB( ).?
在△ADB与△BCA中,
因为∠DBA= (已知),?
AB=BA( ),∠DAB=∠CBA,?
所以△ADB≌△BCA( ),?
所以AD=BC( ).?
三、解答题
9.如图,点A,B,C,D在同一条直线上,AB=FC,∠A=∠F,∠EBC=∠FCB.
试说明:△ABE≌△FCD.
10.如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.试说明:BD=CE.
11.如图,点B,F,C,E在同一条直线上,FB=CE,AB∥DE,AC∥DF,AD交BE于点O.
试说明:(1)△ABC≌△DEF;
(2)AO=DO.
12.如图K-32-12,AD∥BC,AB⊥BC,AB=AD,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)请写出线段BF,EF,DE三者之间的数量关系,并说明理由.
13、(1)如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.试说明:DE=BD+CE.
(2)如图②,将(1)中的条件改为在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,则结论DE=BD+CE是否仍然成立?请说明理由.
1.B 2.D 3.C
4.△ACE AAS
5.∠A=∠D
6.[答案]
5
[解析]
因为AC⊥BC,DE⊥AC,AD⊥AB,所以∠C=∠DEA=∠BAD=90°,所以∠D+∠DAE=90°,∠DAE+∠BAC=90°,所以∠D=∠BAC.在△ACB和△DEA中,因为∠BAC=∠D,∠C=∠DEA,BC=AE,所以△ACB≌△DEA(AAS),所以AB=DA=5.故答案为5.
7.6
8.等式的性质 ∠CAB 公共边 ASA 全等三角形的对应边相等
9.解:因为∠EBC=∠FCB,∠EBC+∠ABE=180°,∠FCB+∠FCD=180°,
所以∠ABE=∠FCD.
在△ABE与△FCD中,
因为∠A=∠F,AB=FC,∠ABE=∠FCD,
所以△ABE≌△FCD(ASA).
10.解:因为AB⊥AC,AD⊥AE,
所以∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,
所以∠CAE=∠BAD.
在△ABD和△ACE中,
因为∠BAD=∠CAE,AB=AC,∠ABD=∠ACE,
所以△ABD≌△ACE(ASA),所以BD=CE.
11.解:(1)因为AB∥DE,所以∠B=∠E.
因为AC∥DF,所以∠BCA=∠EFD.
因为FB=CE,所以BC=EF.
在△ABC和△DEF中,
因为∠B=∠E,BC=EF,∠BCA=∠EFD,
所以△ABC≌△DEF(ASA).
(2)因为△ABC≌△DEF,
所以AC=DF.
在△ACO和△DFO中,
因为∠AOC=∠DOF,∠ACO=∠DFO,AC=DF,
所以△ACO≌△DFO(AAS),所以AO=DO.
12.解:(1)因为AB⊥BC,所以∠ABC=90°.
又因为AD∥BC,所以∠BAD=90°,
即∠BAF+∠DAE=90°.
因为DE⊥AC,所以∠DEA=90°,
所以∠DAE+∠ADE=90°,
所以∠ADE=∠BAF.
因为BF⊥AC,∠ABF=63°,
所以∠ADE=∠BAF=90°-63°=27°.
(2)DE=BF+EF.
理由:因为DE⊥AC,BF⊥AC,
所以∠BFA=∠AED=90°.
在△ABF和△DAE中,
因为∠BFA=∠AED,∠BAF=∠ADE,AB=DA,
所以△ABF≌△DAE(AAS),
所以BF=AE,AF=DE.
因为AF=AE+EF,
所以DE=BF+EF.
[素养提升]
解:(1)因为BD⊥直线m,CE⊥直线m,
所以∠BDA=∠AEC=90°,
所以∠BAD+∠ABD=90°.
因为∠BAC=90°,
所以∠BAD+∠CAE=90°,
所以∠CAE=∠ABD.
在△ADB和△CEA中,
因为∠ABD=∠CAE,∠BDA=∠AEC,AB=CA,
所以△ADB≌△CEA(AAS),
所以BD=AE,AD=CE,
所以DE=AE+AD=BD+CE.
(2)成立.理由:因为∠BDA=∠BAC=α,
所以∠DBA+∠BAD=∠BAD+∠EAC=180°-α,
所以∠EAC=∠DBA.
在△ADB和△CEA中,
因为∠DBA=∠EAC,∠BDA=∠AEC,AB=CA,
所以△ADB≌△CEA(AAS),
所以BD=AE,AD=CE,
所以DE=AE+AD=BD+CE.
一、选择题
1.如图,∠ADB=∠CDB,∠ABD=∠CBD,则直接判定△ABD≌△CBD的依据是
( )
A.SSS
B.ASA
C.AAS
D.以上均不正确
2.如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是
( )
A.0.5
B.1
C.1.5
D.2
3.如图,在△ABC中,F为AC的中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为
( )
A.相等
B.平行
C.平行且相等
D.以上均不正确
二、填空题
4.如图,AE=AD,∠B=∠C,则△ABD≌ ,理由是 .?
5.如图,∠1=∠2,BC=EC,请补充一个条件: ,能根据“AAS”判定△ABC≌△DEC.?
6.如图,AC⊥BC于点C,DE⊥AC于点E,AD⊥AB于点A.若BC=AE,AD=5,则AB= .?
7.如图,AB∥CD,AB=CD,AD∥BC,AD=BC,BD,AC交于点O,EF是过点O的线段,分别交AD,BC于点E,F,则图中的全等三角形有 对.?
8.如图,已知∠CAB=∠DBA,∠CBD=∠DAC,请将下面说明AD=BC的过程和理由补充完整.
解:因为∠DBA=∠CAB,∠CBD=∠DAC,
所以∠CBD+∠DBA=∠DAC+∠CAB,
所以∠CBA=∠DAB( ).?
在△ADB与△BCA中,
因为∠DBA= (已知),?
AB=BA( ),∠DAB=∠CBA,?
所以△ADB≌△BCA( ),?
所以AD=BC( ).?
三、解答题
9.如图,点A,B,C,D在同一条直线上,AB=FC,∠A=∠F,∠EBC=∠FCB.
试说明:△ABE≌△FCD.
10.如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.试说明:BD=CE.
11.如图,点B,F,C,E在同一条直线上,FB=CE,AB∥DE,AC∥DF,AD交BE于点O.
试说明:(1)△ABC≌△DEF;
(2)AO=DO.
12.如图K-32-12,AD∥BC,AB⊥BC,AB=AD,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)请写出线段BF,EF,DE三者之间的数量关系,并说明理由.
13、(1)如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.试说明:DE=BD+CE.
(2)如图②,将(1)中的条件改为在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,则结论DE=BD+CE是否仍然成立?请说明理由.
1.B 2.D 3.C
4.△ACE AAS
5.∠A=∠D
6.[答案]
5
[解析]
因为AC⊥BC,DE⊥AC,AD⊥AB,所以∠C=∠DEA=∠BAD=90°,所以∠D+∠DAE=90°,∠DAE+∠BAC=90°,所以∠D=∠BAC.在△ACB和△DEA中,因为∠BAC=∠D,∠C=∠DEA,BC=AE,所以△ACB≌△DEA(AAS),所以AB=DA=5.故答案为5.
7.6
8.等式的性质 ∠CAB 公共边 ASA 全等三角形的对应边相等
9.解:因为∠EBC=∠FCB,∠EBC+∠ABE=180°,∠FCB+∠FCD=180°,
所以∠ABE=∠FCD.
在△ABE与△FCD中,
因为∠A=∠F,AB=FC,∠ABE=∠FCD,
所以△ABE≌△FCD(ASA).
10.解:因为AB⊥AC,AD⊥AE,
所以∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,
所以∠CAE=∠BAD.
在△ABD和△ACE中,
因为∠BAD=∠CAE,AB=AC,∠ABD=∠ACE,
所以△ABD≌△ACE(ASA),所以BD=CE.
11.解:(1)因为AB∥DE,所以∠B=∠E.
因为AC∥DF,所以∠BCA=∠EFD.
因为FB=CE,所以BC=EF.
在△ABC和△DEF中,
因为∠B=∠E,BC=EF,∠BCA=∠EFD,
所以△ABC≌△DEF(ASA).
(2)因为△ABC≌△DEF,
所以AC=DF.
在△ACO和△DFO中,
因为∠AOC=∠DOF,∠ACO=∠DFO,AC=DF,
所以△ACO≌△DFO(AAS),所以AO=DO.
12.解:(1)因为AB⊥BC,所以∠ABC=90°.
又因为AD∥BC,所以∠BAD=90°,
即∠BAF+∠DAE=90°.
因为DE⊥AC,所以∠DEA=90°,
所以∠DAE+∠ADE=90°,
所以∠ADE=∠BAF.
因为BF⊥AC,∠ABF=63°,
所以∠ADE=∠BAF=90°-63°=27°.
(2)DE=BF+EF.
理由:因为DE⊥AC,BF⊥AC,
所以∠BFA=∠AED=90°.
在△ABF和△DAE中,
因为∠BFA=∠AED,∠BAF=∠ADE,AB=DA,
所以△ABF≌△DAE(AAS),
所以BF=AE,AF=DE.
因为AF=AE+EF,
所以DE=BF+EF.
[素养提升]
解:(1)因为BD⊥直线m,CE⊥直线m,
所以∠BDA=∠AEC=90°,
所以∠BAD+∠ABD=90°.
因为∠BAC=90°,
所以∠BAD+∠CAE=90°,
所以∠CAE=∠ABD.
在△ADB和△CEA中,
因为∠ABD=∠CAE,∠BDA=∠AEC,AB=CA,
所以△ADB≌△CEA(AAS),
所以BD=AE,AD=CE,
所以DE=AE+AD=BD+CE.
(2)成立.理由:因为∠BDA=∠BAC=α,
所以∠DBA+∠BAD=∠BAD+∠EAC=180°-α,
所以∠EAC=∠DBA.
在△ADB和△CEA中,
因为∠DBA=∠EAC,∠BDA=∠AEC,AB=CA,
所以△ADB≌△CEA(AAS),
所以BD=AE,AD=CE,
所以DE=AE+AD=BD+CE.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
