7.1 行星的运动 教学设计
文档属性
| 名称 | 7.1 行星的运动 教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-21 15:21:29 | ||
图片预览

文档简介
行星的运动
一、教学思路
二、教学活动
任务1:探究行星绕谁运动
问题情景:阅读本节教材第一段及“科学漫步”内容。
问题
1.在古代,人们通过什么方式认识行星的运动?有哪些比较典型的学说(模型)?代表人物及内容?
2.“地心说”为什么当时得到很多人的认可?
3.哥白尼提出“日心说”,是基于怎样的信仰?
4.继“日心说”后,又有哪些代表人物为行星运动的研究做出了巨大贡献?
5.你觉得第谷的可贵之处是什么?开普勒获得成功的因素有哪些?
教学建议:
(1)思维引导建议:“地心说”的代表人物是古希腊的托勒密,他认为地球是宇宙的中心,是静止不动的,太阳、月亮以及其他行星都绕地球运动。“日心说”的代表人物是波兰的哥白尼,他认为太阳是静止不动的,地球和其他行星是绕太阳运动的。由于“地心说”比较符合人们的直接经验,同时也符合势力强大的宗教神学关于地球是宇宙中心的认识,故“地心说”一度占据了统治地位。到了哥白尼时代,“地心说”所描述的天体的运动不仅复杂而且问题很多,哥白尼认为宇宙是美的,而美的东西一定是简单和谐的,故大胆地提出“日心说”,使行星运动的描述变得简单。继“日心说”后,第谷连续21年对777颗恒星的位置进行精确测量,在他以前,人们观测天体位置的误差大约是,第谷把这个不确定性减小到;开普勒从相信“行星绕太阳做匀速圆周运动的观点”开始思考问题,到对火星轨道“70余次尝试所得的结果都与第谷的观测数据有至少的角度偏差”,从而对“圆轨道”表示怀疑,4年多的计算否定掉了19种行星轨道设想直至确立“椭圆轨道”。
(2)教学活动建议:为节约课堂教学时间,可以在课前布置阅读本节教材的学习任务(包括问题)。对问题1、2、3、4,学生可采用独立回答的方式,其他同学补充;对问题5,可以先让学生小组讨论,然后各组进行交流,教师适当进行点拨和说明。
任务2:探究行星运动的轨道是怎样的
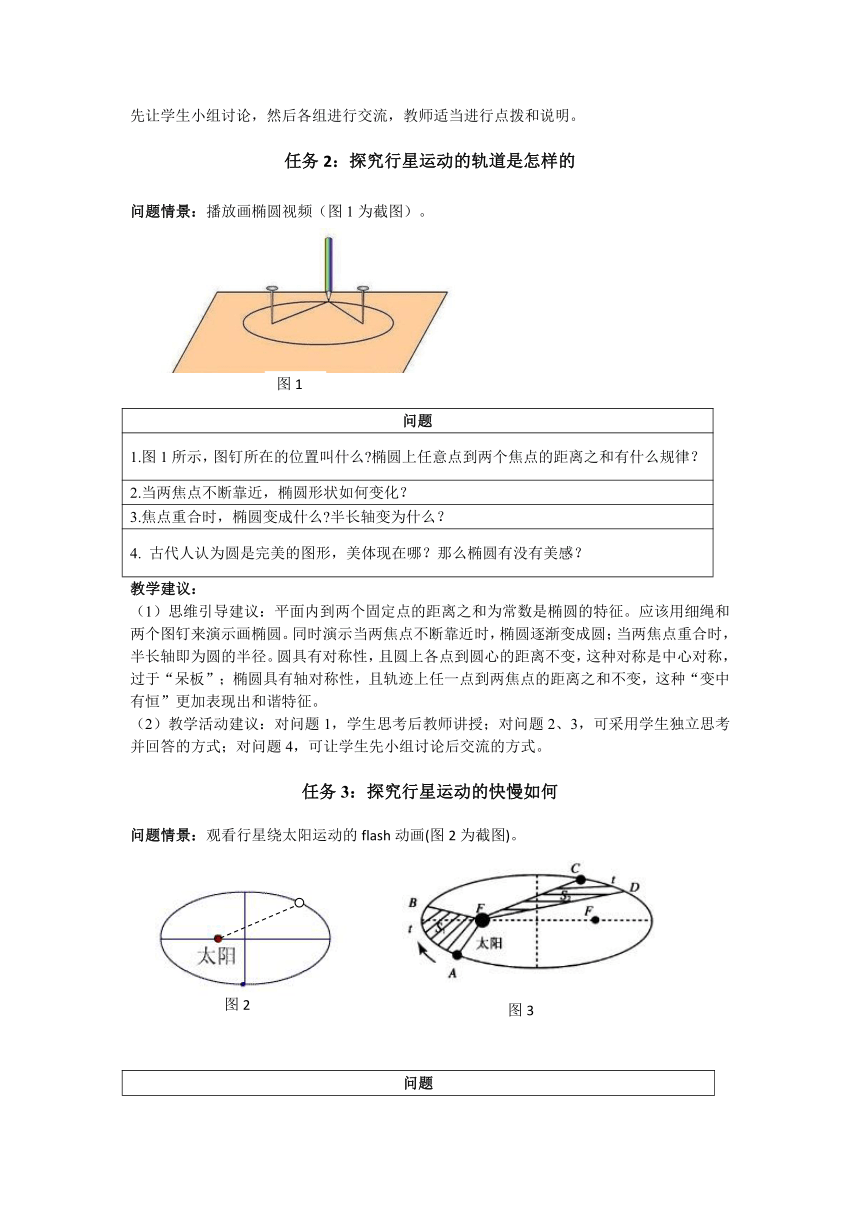
问题情景:播放画椭圆视频(图1为截图)。
问题
1.图1所示,图钉所在的位置叫什么?椭圆上任意点到两个焦点的距离之和有什么规律?
2.当两焦点不断靠近,椭圆形状如何变化?
3.焦点重合时,椭圆变成什么?半长轴变为什么?
4. 古代人认为圆是完美的图形,美体现在哪?那么椭圆有没有美感?
教学建议:
(1)思维引导建议:平面内到两个固定点的距离之和为常数是椭圆的特征。应该用细绳和两个图钉来演示画椭圆。同时演示当两焦点不断靠近时,椭圆逐渐变成圆;当两焦点重合时,半长轴即为圆的半径。圆具有对称性,且圆上各点到圆心的距离不变,这种对称是中心对称,过于“呆板”;椭圆具有轴对称性,且轨迹上任一点到两焦点的距离之和不变,这种“变中有恒”更加表现出和谐特征。
(2)教学活动建议:对问题1,学生思考后教师讲授;对问题2、3,可采用学生独立思考并回答的方式;对问题4,可让学生先小组讨论后交流的方式。
任务3:探究行星运动的快慢如何
问题情景:观看行星绕太阳运动的flash动画(图2为截图)。
问题
1.所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上,这是开普勒第一定律。如图2行星沿椭圆轨道运动,行星运动的速度大小还保持不变吗?通过观察动画,你有什么发现?
2.开普勒第二定律指出太阳和行星的连线在相等的时间内所扫过的面积相等。如图3,你是否能够证明近日点的速率大于远日点的速率?
教学建议:
(1) 思维引导建议:开普勒第二定律指出行星运动快慢的定量关系。据此定律,由几何关系可知,当行星在近日点时,距离小,则相同时间内走过的弧长长,所以行星运动快;当行星在远日点时,距离大,则相同时间内走过的弧长短,所以行星运动慢。
(2)教学活动建议:对问题1,可采用学生独立思考并回答的方式;对问题2,可采用学生自己分析推理的方式。对于基础比较好的同学,课后还可以试着讨论近日点与远日点的角速度大小,看看能否发现开普勒第二定律蕴含着的行星绕太阳公转的角动量守恒规律。
任务4:探究行星运动的周期与什么有关
问题情景:(1)观看太阳系中各大行星的动态模拟视频(图3为截图)
(2)展示表格(表格1)(表中把地球公转周期作为一个时间单位,把地球轨道的半长轴作为一个长度单位)
行星 周期T 半长轴
水星 0.241 0.383
金星 0.616 0.725
地球 1.000 1.000
火星 1.882 1.530
木星 11.871 5.221
土星 29.477 9.53
天王星 84 19.26
问题
1.观看太阳系中各大行星的动态模拟视频,各行星周期T相同吗?周期大小与离太阳远近有关吗?越远的行星周期是否越大?
2.假如表1是第谷的观测数据,你是开普勒,你将如何寻找T与的关系?你是尝试T与的乘积寻找关系,还是T与之比寻找关系?理由是什么?
3.尝试,看是否有什么规律?开普勒发现这一规律时是怎样一种心情?
4.这一定量反映周期与半长轴关系的规律称为开普勒第三定律,k对所有行星都相同,说明跟行星无关,它会跟谁有关呢?
5.太阳系行星的运动轨道是否很接近圆?若视作圆轨道,开普勒第三定律又如何表述?
教学建议:
(1)思维引导建议:
各大行星绕太阳运动,半长轴不同,周期也不同。开普勒坚信周期与半长轴之间应该存在着简单而完美的规律。本着这一信念,他用了10年的时间才找到它们之间的关系。这一结果发表在1619年出版的《宇宙的和谐论》中,它蕴含着行星运动的动力学关系,开普勒也由此被尊称为“天空的立法者”。
(2)数据处理建议:由于a大,T也大,从a与T乘积的角度显然不能找到不变量,可以尝试,相关数据如表2所示。
表 2
行星 T a
水星 0.241 0.383 0.058 0.014 0.147 0.056
金星 0.616 0.725 0.379 0.234 0.526 0.381
地球 1.000 1.000 1.000 1.000 1.000 1.000
火星 1.882 1.530 3.54 6.67 2.34 3.58
木星 11.871 5.221 140.9 1673 27.3 142.3
土星 29.477 9.53 868.9 25612 90.8 865.5
天王星 84 19.26 7056 592704 370.9 7144
(3)教学活动建议:对问题1,可让学生独立回答,其他同学补充完善;对问题2,可以在学生独立思考的基础上小组讨论并回答,教师根据需要点拨;对问题3,建议分小组进行数据运算,完成后交流分享探究结果;对问题4,有一定的开放性,可让不同学生发表看法;对问题5,可让学生独立思考后回答。
一、教学思路
二、教学活动
任务1:探究行星绕谁运动
问题情景:阅读本节教材第一段及“科学漫步”内容。
问题
1.在古代,人们通过什么方式认识行星的运动?有哪些比较典型的学说(模型)?代表人物及内容?
2.“地心说”为什么当时得到很多人的认可?
3.哥白尼提出“日心说”,是基于怎样的信仰?
4.继“日心说”后,又有哪些代表人物为行星运动的研究做出了巨大贡献?
5.你觉得第谷的可贵之处是什么?开普勒获得成功的因素有哪些?
教学建议:
(1)思维引导建议:“地心说”的代表人物是古希腊的托勒密,他认为地球是宇宙的中心,是静止不动的,太阳、月亮以及其他行星都绕地球运动。“日心说”的代表人物是波兰的哥白尼,他认为太阳是静止不动的,地球和其他行星是绕太阳运动的。由于“地心说”比较符合人们的直接经验,同时也符合势力强大的宗教神学关于地球是宇宙中心的认识,故“地心说”一度占据了统治地位。到了哥白尼时代,“地心说”所描述的天体的运动不仅复杂而且问题很多,哥白尼认为宇宙是美的,而美的东西一定是简单和谐的,故大胆地提出“日心说”,使行星运动的描述变得简单。继“日心说”后,第谷连续21年对777颗恒星的位置进行精确测量,在他以前,人们观测天体位置的误差大约是,第谷把这个不确定性减小到;开普勒从相信“行星绕太阳做匀速圆周运动的观点”开始思考问题,到对火星轨道“70余次尝试所得的结果都与第谷的观测数据有至少的角度偏差”,从而对“圆轨道”表示怀疑,4年多的计算否定掉了19种行星轨道设想直至确立“椭圆轨道”。
(2)教学活动建议:为节约课堂教学时间,可以在课前布置阅读本节教材的学习任务(包括问题)。对问题1、2、3、4,学生可采用独立回答的方式,其他同学补充;对问题5,可以先让学生小组讨论,然后各组进行交流,教师适当进行点拨和说明。
任务2:探究行星运动的轨道是怎样的
问题情景:播放画椭圆视频(图1为截图)。
问题
1.图1所示,图钉所在的位置叫什么?椭圆上任意点到两个焦点的距离之和有什么规律?
2.当两焦点不断靠近,椭圆形状如何变化?
3.焦点重合时,椭圆变成什么?半长轴变为什么?
4. 古代人认为圆是完美的图形,美体现在哪?那么椭圆有没有美感?
教学建议:
(1)思维引导建议:平面内到两个固定点的距离之和为常数是椭圆的特征。应该用细绳和两个图钉来演示画椭圆。同时演示当两焦点不断靠近时,椭圆逐渐变成圆;当两焦点重合时,半长轴即为圆的半径。圆具有对称性,且圆上各点到圆心的距离不变,这种对称是中心对称,过于“呆板”;椭圆具有轴对称性,且轨迹上任一点到两焦点的距离之和不变,这种“变中有恒”更加表现出和谐特征。
(2)教学活动建议:对问题1,学生思考后教师讲授;对问题2、3,可采用学生独立思考并回答的方式;对问题4,可让学生先小组讨论后交流的方式。
任务3:探究行星运动的快慢如何
问题情景:观看行星绕太阳运动的flash动画(图2为截图)。
问题
1.所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上,这是开普勒第一定律。如图2行星沿椭圆轨道运动,行星运动的速度大小还保持不变吗?通过观察动画,你有什么发现?
2.开普勒第二定律指出太阳和行星的连线在相等的时间内所扫过的面积相等。如图3,你是否能够证明近日点的速率大于远日点的速率?
教学建议:
(1) 思维引导建议:开普勒第二定律指出行星运动快慢的定量关系。据此定律,由几何关系可知,当行星在近日点时,距离小,则相同时间内走过的弧长长,所以行星运动快;当行星在远日点时,距离大,则相同时间内走过的弧长短,所以行星运动慢。
(2)教学活动建议:对问题1,可采用学生独立思考并回答的方式;对问题2,可采用学生自己分析推理的方式。对于基础比较好的同学,课后还可以试着讨论近日点与远日点的角速度大小,看看能否发现开普勒第二定律蕴含着的行星绕太阳公转的角动量守恒规律。
任务4:探究行星运动的周期与什么有关
问题情景:(1)观看太阳系中各大行星的动态模拟视频(图3为截图)
(2)展示表格(表格1)(表中把地球公转周期作为一个时间单位,把地球轨道的半长轴作为一个长度单位)
行星 周期T 半长轴
水星 0.241 0.383
金星 0.616 0.725
地球 1.000 1.000
火星 1.882 1.530
木星 11.871 5.221
土星 29.477 9.53
天王星 84 19.26
问题
1.观看太阳系中各大行星的动态模拟视频,各行星周期T相同吗?周期大小与离太阳远近有关吗?越远的行星周期是否越大?
2.假如表1是第谷的观测数据,你是开普勒,你将如何寻找T与的关系?你是尝试T与的乘积寻找关系,还是T与之比寻找关系?理由是什么?
3.尝试,看是否有什么规律?开普勒发现这一规律时是怎样一种心情?
4.这一定量反映周期与半长轴关系的规律称为开普勒第三定律,k对所有行星都相同,说明跟行星无关,它会跟谁有关呢?
5.太阳系行星的运动轨道是否很接近圆?若视作圆轨道,开普勒第三定律又如何表述?
教学建议:
(1)思维引导建议:
各大行星绕太阳运动,半长轴不同,周期也不同。开普勒坚信周期与半长轴之间应该存在着简单而完美的规律。本着这一信念,他用了10年的时间才找到它们之间的关系。这一结果发表在1619年出版的《宇宙的和谐论》中,它蕴含着行星运动的动力学关系,开普勒也由此被尊称为“天空的立法者”。
(2)数据处理建议:由于a大,T也大,从a与T乘积的角度显然不能找到不变量,可以尝试,相关数据如表2所示。
表 2
行星 T a
水星 0.241 0.383 0.058 0.014 0.147 0.056
金星 0.616 0.725 0.379 0.234 0.526 0.381
地球 1.000 1.000 1.000 1.000 1.000 1.000
火星 1.882 1.530 3.54 6.67 2.34 3.58
木星 11.871 5.221 140.9 1673 27.3 142.3
土星 29.477 9.53 868.9 25612 90.8 865.5
天王星 84 19.26 7056 592704 370.9 7144
(3)教学活动建议:对问题1,可让学生独立回答,其他同学补充完善;对问题2,可以在学生独立思考的基础上小组讨论并回答,教师根据需要点拨;对问题3,建议分小组进行数据运算,完成后交流分享探究结果;对问题4,有一定的开放性,可让不同学生发表看法;对问题5,可让学生独立思考后回答。
