6.1.1函数的平均变化率同步 习题2020-2021学年高二下学期数学人教B版(2019)选择性必修第三册Word含解析
文档属性
| 名称 | 6.1.1函数的平均变化率同步 习题2020-2021学年高二下学期数学人教B版(2019)选择性必修第三册Word含解析 |
|
|
| 格式 | doc | ||
| 文件大小 | 52.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 14:55:47 | ||
图片预览



文档简介
函数的平均变化率
一、选择题
1.函数f(x)=x2-1在区间[1,m]上的平均变化率为3,则实数m的值为( )
A.3 B.2
C.1 D.4
2.已知函数y=f(x)=x2+1,则在x=2,Δx=0.1时,Δy的值为( )
A.0.40 B.0.41
C.0.43 D.0.44
3.已知函数f(x)=2x2-4的图像上一点(1,-2)及附近一点(1+Δx,-2+Δy),则=( )
A.4 B.4x
C.4+2Δx D.4+2(Δx)2
4.一质点的运动方程是s=5-3t2,则在一段时间[1,1+Δt]内相应的平均速度为( )
A.3Δt+6 B.-3Δt+6
C.3Δt-6 D.-3Δt-6
二、填空题
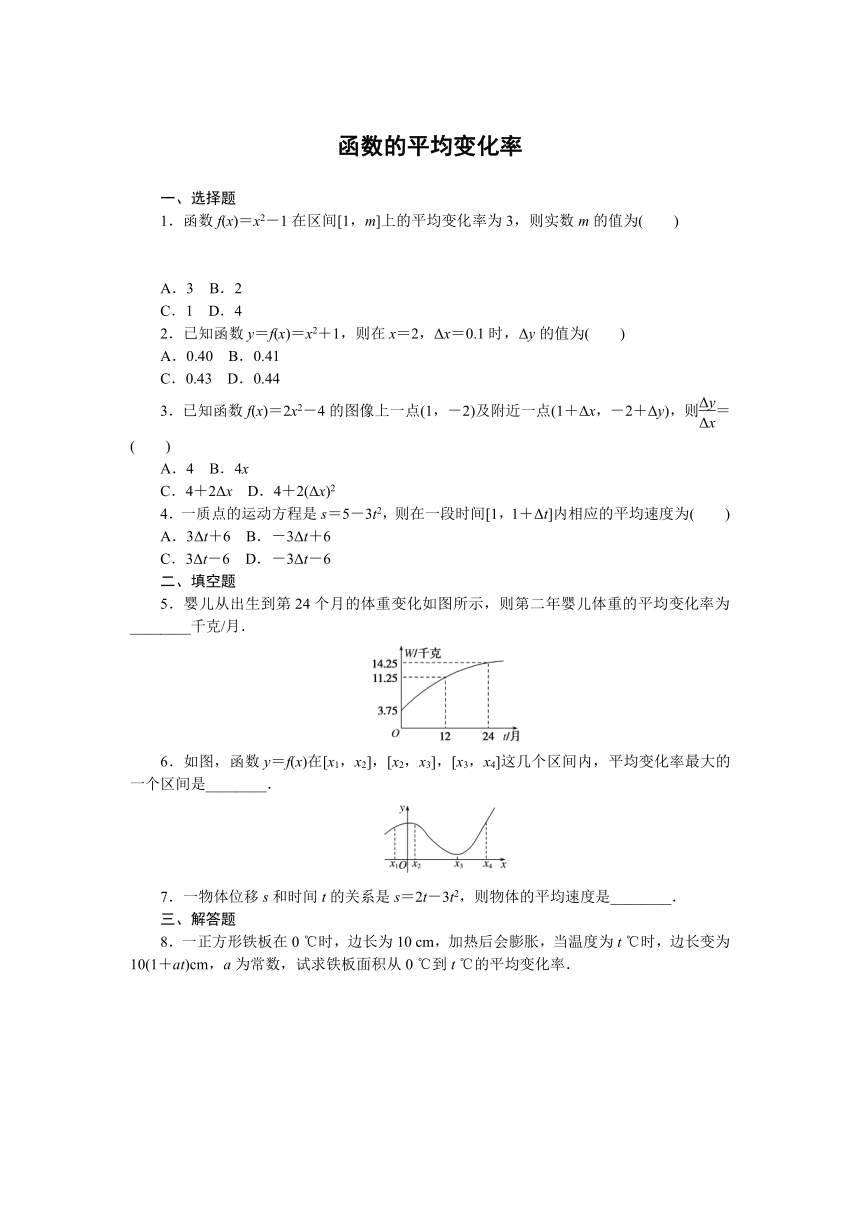
5.婴儿从出生到第24个月的体重变化如图所示,则第二年婴儿体重的平均变化率为________千克/月.
6.如图,函数y=f(x)在[x1,x2],[x2,x3],[x3,x4]这几个区间内,平均变化率最大的一个区间是________.
7.一物体位移s和时间t的关系是s=2t-3t2,则物体的平均速度是________.
三、解答题
8.一正方形铁板在0 ℃时,边长为10 cm,加热后会膨胀,当温度为t ℃时,边长变为10(1+at)cm,a为常数,试求铁板面积从0 ℃到t ℃的平均变化率.
9.已知某物体按照s(t)=3t2+t+4(t的单位:s,s的单位:m)的规律做直线运动,求该物体在4 s附近的平均速度.
10.在x=1附近,取Δx=0.3,关于下列说法正确的有________.
①y=x平均变化率为1
②y=x2平均变化率为2.3
③y=x3平均变化率为3.99
④y=平均变化率为0.3
1.解析:由已知得:=3,
∴m+1=3,∴m=2.
答案:B
2.解析:∵x=2,Δx=0.1,
∴Δy=f(2+0.1)-f(2)=2.12-22=0.41.
答案:B
3.解析:因为Δy=f(1+Δx)-f(1)=2(1+Δx)2-4-(2×12-4)=4Δx+2(Δx)2,
所以==4+2Δx.
答案:C
4.解析:平均速度为
==-3Δt-6,
故选D.
答案:D
5.解析: 第二年婴儿体重的平均变化率为=0.25(千克/月).
答案:0.25
6.解析:由平均变化率的定义可知,函数y=f(x)在区间[x1,x2],[x2,x3],[x3,x4]上平均变化率分别为,,,结合图像可以发现函数y=f(x)的平均变化率最大的一个区间是[x3,x4].
答案:[x3,x4]
7.解析:
=
=
=2-6t-3Δt.
所以物体的平均速度是:2-6t-3Δt
答案: 2-6t-3Δt
8.解析:铁板面积S的增量ΔS=102(1+at)2-102=100(2at+a2t2),
因此铁板面积从0 ℃到t ℃的平均变化率为==100(2a+a2t).
9.解析:==
=
=(25+3Δt)m/s,
即该物体在4 s附近的平均速度为(25+3Δt)m/s.
10.解析:根据平均变化率的计算公式,可得=,
所以在x=1附近取Δx=0.3,则平均变化率的公式为=,
①的平均变化率为=1,正确;
②的平均变化率为=2.3,正确;
③的平均变化率为=3.99,正确;
④的平均变化率为≈-0.77,错误.
答案:①②③
一、选择题
1.函数f(x)=x2-1在区间[1,m]上的平均变化率为3,则实数m的值为( )
A.3 B.2
C.1 D.4
2.已知函数y=f(x)=x2+1,则在x=2,Δx=0.1时,Δy的值为( )
A.0.40 B.0.41
C.0.43 D.0.44
3.已知函数f(x)=2x2-4的图像上一点(1,-2)及附近一点(1+Δx,-2+Δy),则=( )
A.4 B.4x
C.4+2Δx D.4+2(Δx)2
4.一质点的运动方程是s=5-3t2,则在一段时间[1,1+Δt]内相应的平均速度为( )
A.3Δt+6 B.-3Δt+6
C.3Δt-6 D.-3Δt-6
二、填空题
5.婴儿从出生到第24个月的体重变化如图所示,则第二年婴儿体重的平均变化率为________千克/月.
6.如图,函数y=f(x)在[x1,x2],[x2,x3],[x3,x4]这几个区间内,平均变化率最大的一个区间是________.
7.一物体位移s和时间t的关系是s=2t-3t2,则物体的平均速度是________.
三、解答题
8.一正方形铁板在0 ℃时,边长为10 cm,加热后会膨胀,当温度为t ℃时,边长变为10(1+at)cm,a为常数,试求铁板面积从0 ℃到t ℃的平均变化率.
9.已知某物体按照s(t)=3t2+t+4(t的单位:s,s的单位:m)的规律做直线运动,求该物体在4 s附近的平均速度.
10.在x=1附近,取Δx=0.3,关于下列说法正确的有________.
①y=x平均变化率为1
②y=x2平均变化率为2.3
③y=x3平均变化率为3.99
④y=平均变化率为0.3
1.解析:由已知得:=3,
∴m+1=3,∴m=2.
答案:B
2.解析:∵x=2,Δx=0.1,
∴Δy=f(2+0.1)-f(2)=2.12-22=0.41.
答案:B
3.解析:因为Δy=f(1+Δx)-f(1)=2(1+Δx)2-4-(2×12-4)=4Δx+2(Δx)2,
所以==4+2Δx.
答案:C
4.解析:平均速度为
==-3Δt-6,
故选D.
答案:D
5.解析: 第二年婴儿体重的平均变化率为=0.25(千克/月).
答案:0.25
6.解析:由平均变化率的定义可知,函数y=f(x)在区间[x1,x2],[x2,x3],[x3,x4]上平均变化率分别为,,,结合图像可以发现函数y=f(x)的平均变化率最大的一个区间是[x3,x4].
答案:[x3,x4]
7.解析:
=
=
=2-6t-3Δt.
所以物体的平均速度是:2-6t-3Δt
答案: 2-6t-3Δt
8.解析:铁板面积S的增量ΔS=102(1+at)2-102=100(2at+a2t2),
因此铁板面积从0 ℃到t ℃的平均变化率为==100(2a+a2t).
9.解析:==
=
=(25+3Δt)m/s,
即该物体在4 s附近的平均速度为(25+3Δt)m/s.
10.解析:根据平均变化率的计算公式,可得=,
所以在x=1附近取Δx=0.3,则平均变化率的公式为=,
①的平均变化率为=1,正确;
②的平均变化率为=2.3,正确;
③的平均变化率为=3.99,正确;
④的平均变化率为≈-0.77,错误.
答案:①②③
