第7章二项分布、超几何分布、正态分布综合复习-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(16张PPT)
文档属性
| 名称 | 第7章二项分布、超几何分布、正态分布综合复习-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 804.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 20:53:24 | ||
图片预览



文档简介
二项分布、超几何分布、正态分布综合复习
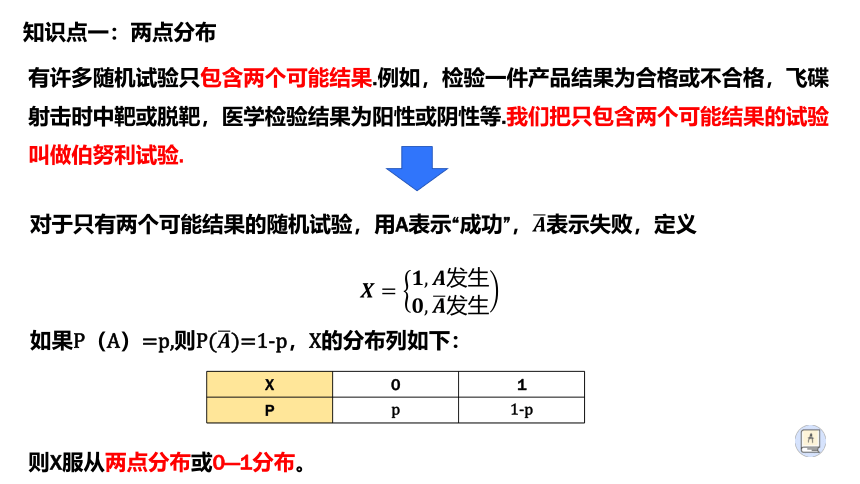
知识点一:两点分布
对于只有两个可能结果的随机试验,用A表示“成功”,????表示失败,定义
????=????,????发生????,????发生
如果P(A)=p,则P(????)=1-p,X的分布列如下:
?
{5940675A-B579-460E-94D1-54222C63F5DA}X
0
1
P
p
1-p
则X服从两点分布或0—1分布。
有许多随机试验只包含两个可能结果.例如,检验一件产品结果为合格或不合格,飞碟射击时中靶或脱靶,医学检验结果为阳性或阴性等.我们把只包含两个可能结果的试验叫做伯努利试验.
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0如果随机变量X的分布列具有上式的形式,则称随机变量X服从二项分布(binomial distribution),记作X~B(n,p).
?
一般地,如果X~B(n,p),那么E(X)=np; D(X)=np(1-p).
知识点二:二项分布
我们将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验。
知识点三:超几何分布
一般地,假设一批产品共有N件,其中有M件次品,从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品的次品数,则X的分布列为
其中n,M,N∈N*,m=max{0,n-N+M},r=min{n,M}.如果随机变量X的分布列具有上式的形式,那么称随机变量X服从超几何分布。
,k=m,m+1,m+2,...,r.
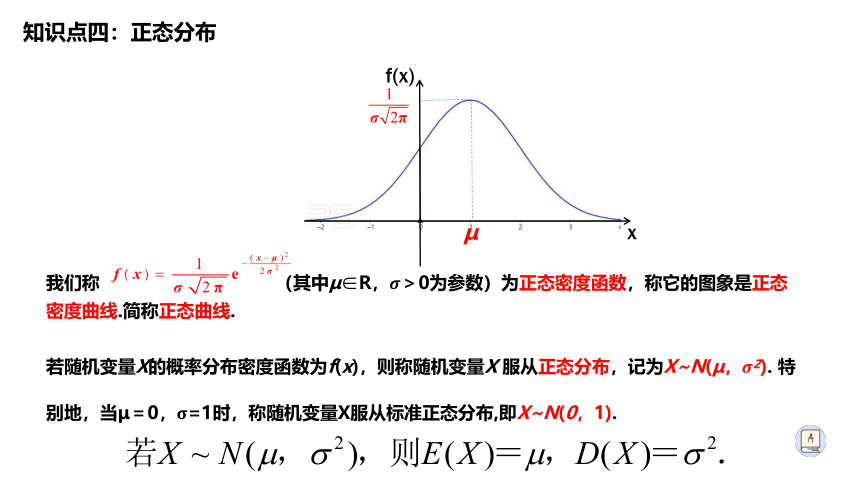
我们称 (其中μ∈R,????>0为参数)为正态密度函数,称它的图象是正态密度曲线.简称正态曲线.
若随机变量X的概率分布密度函数为f(x),则称随机变量X 服从正态分布,记为X~N(μ,????2). 特别地,当μ=0,????=1时,称随机变量X服从标准正态分布,即X~N(0,1).
?
μ
x
f(x)
知识点四:正态分布
μ
x
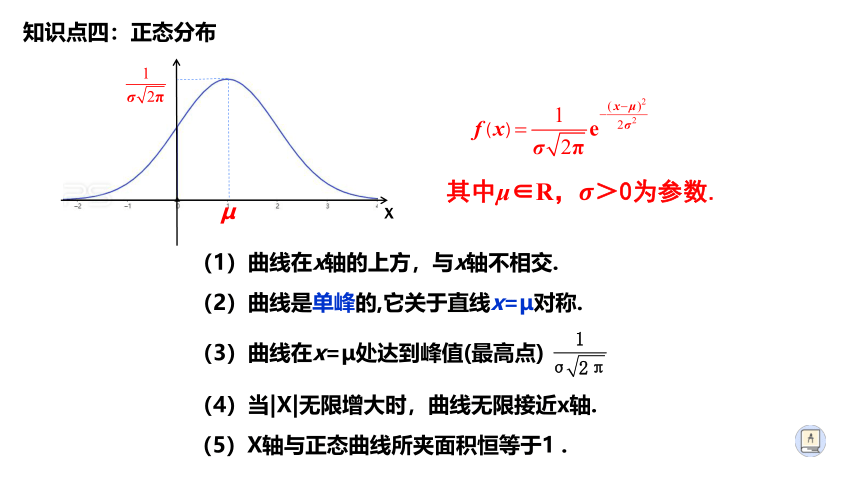
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(4)当|X|无限增大时,曲线无限接近x轴.
(3)曲线在x=μ处达到峰值(最高点)
其中μ∈R,????>0为参数.
?
(5)X轴与正态曲线所夹面积恒等于1 .
知识点四:正态分布
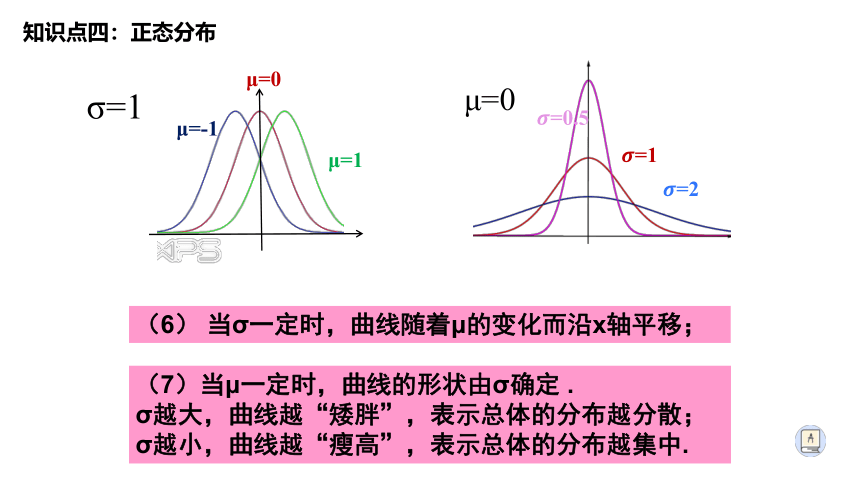
知识点四:正态分布
μ=-1
μ=0
μ=1
σ=1
μ=0
????=0.5
?
????=1
?
????=2
?
(7)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
(6) 当σ一定时,曲线随着μ的变化而沿x轴平移;
题型一:二项分布
题型一:二项分布
题型二:超几何分布
题型三: 正态分布
知识点一:两点分布
对于只有两个可能结果的随机试验,用A表示“成功”,????表示失败,定义
????=????,????发生????,????发生
如果P(A)=p,则P(????)=1-p,X的分布列如下:
?
{5940675A-B579-460E-94D1-54222C63F5DA}X
0
1
P
p
1-p
则X服从两点分布或0—1分布。
有许多随机试验只包含两个可能结果.例如,检验一件产品结果为合格或不合格,飞碟射击时中靶或脱靶,医学检验结果为阳性或阴性等.我们把只包含两个可能结果的试验叫做伯努利试验.
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0
?
一般地,如果X~B(n,p),那么E(X)=np; D(X)=np(1-p).
知识点二:二项分布
我们将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验。
知识点三:超几何分布
一般地,假设一批产品共有N件,其中有M件次品,从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品的次品数,则X的分布列为
其中n,M,N∈N*,m=max{0,n-N+M},r=min{n,M}.如果随机变量X的分布列具有上式的形式,那么称随机变量X服从超几何分布。
,k=m,m+1,m+2,...,r.
我们称 (其中μ∈R,????>0为参数)为正态密度函数,称它的图象是正态密度曲线.简称正态曲线.
若随机变量X的概率分布密度函数为f(x),则称随机变量X 服从正态分布,记为X~N(μ,????2). 特别地,当μ=0,????=1时,称随机变量X服从标准正态分布,即X~N(0,1).
?
μ
x
f(x)
知识点四:正态分布
μ
x
(1)曲线在x轴的上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(4)当|X|无限增大时,曲线无限接近x轴.
(3)曲线在x=μ处达到峰值(最高点)
其中μ∈R,????>0为参数.
?
(5)X轴与正态曲线所夹面积恒等于1 .
知识点四:正态分布
知识点四:正态分布
μ=-1
μ=0
μ=1
σ=1
μ=0
????=0.5
?
????=1
?
????=2
?
(7)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
(6) 当σ一定时,曲线随着μ的变化而沿x轴平移;
题型一:二项分布
题型一:二项分布
题型二:超几何分布
题型三: 正态分布
