第四单元 一次函数单元测试题(含解析)
图片预览




文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册第四单元
一次函数
单元练习
一、单选题
1.下列各种图象中,y不是x的函数的是(???
)
A.?????????B.?????????C.?????????D.?
2.函数
中自变量
的取值范围是(?
)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
3.直线
不经过的象限是
(???
)
A.?第四象限???????????????????????????B.?第三象限???????????????????????????C.?第二象限???????????????????????????D.?第一象限
4.把直线y=2x﹣1向左平移1个单位,平移后直线的关系式为(?
)
A.?y=2x﹣2???????????????????????????????B.?y=2x+1???????????????????????????????C.?y=2x???????????????????????????????D.?y=2x+2
5.正比例函数y=kx(k≠0)和一次函数y=k(1﹣x)在同一个直角坐标系内的图象大致是下图中的(??
)
A.???????????B.???????????C.???????????D.?
6.已知一次函数
.
若
随
的增大而增大,则
的取值范围是(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
7.正比例函数y=kx(k≠0)的图象经过第二、四象限,则一次函数y=x+k的图象大致是(??
)
A.??????????B.??????????C.??????????D.?
8.已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=4x+2上,则y1
,
y2
,
y3的值的大小关系是(??
)
A.?y3<y1<y2???????????????????????B.?y1<y2<y3???????????????????????C.?y3>y1>y2???????????????????????D.?y1>y2>y3
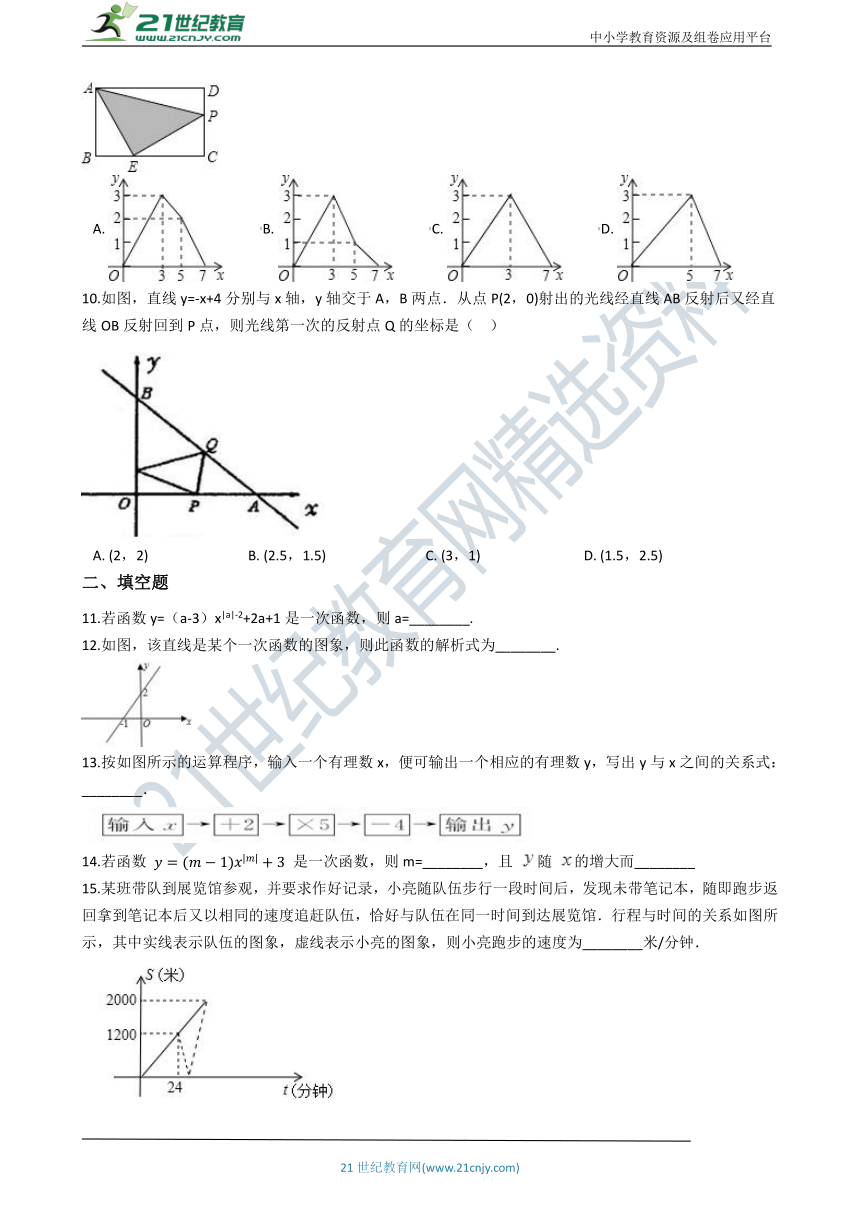
9.如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是(??
)
A.???????????B.???????????C.???????????D.?
10.如图,直线y=-x+4分别与x轴,y轴交于A,B两点.从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是(
??)
A.?(2,2)?????????????????????????????B.?(2.5,1.5)?????????????????????????????C.?(3,1)??????????????????????????????D.?(1.5,2.5)
二、填空题
11.若函数y=(a-3)x|a|-2+2a+1是一次函数,则a=________.
12.如图,该直线是某个一次函数的图象,则此函数的解析式为________.
13.按如图所示的运算程序,输入一个有理数x,便可输出一个相应的有理数y,写出y与x之间的关系式:________.
14.若函数
是一次函数,则m=________,且
随
的增大而________
15.某班带队到展览馆参观,并要求作好记录,小亮随队伍步行一段时间后,发现未带笔记本,随即跑步返回拿到笔记本后又以相同的速度追赶队伍,恰好与队伍在同一时间到达展览馆.行程与时间的关系如图所示,其中实线表示队伍的图象,虚线表示小亮的图象,则小亮跑步的速度为________米/分钟.
三、解答题
16.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
若日销售量y是销售价x的一次函数.
x
(元)
15
20
25
…
y
(件)
25
20
15
…
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
17.已知一次函数
,求:
(1)m为何值时,y随
的增大而减少??
(2)m为何值时,函数图象与y轴的交点在
轴下方?
(3)m为何值时,图象经过第一、三、四象限??
(4)图象能否过第一、二、三象限?
四、综合题
18.某通讯公司推出①、②两种收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
(1)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(2)何时两种收费方式费用相等?
19.小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min的速度从邮局沿同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t
min时,小明与家之间的距离为
S1
m,小明爸爸与家之间的距离为S2
m,图中折线OABD,线段EF分别是表示S1、S2与t之间函数关系的图像.
(1)求S2与t之间的函数关系式:
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
20.如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)求正比例函数与一次函数的关系式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
(4)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
答案解析部分
一、单选题
1.【答案】
B
解:过x轴上一点作x轴的垂线,若与函数图像有且仅有一个交点,则该图像表示函数的图像;若与函数图像有不止一个交点,则该图像不是函数图像.在A.C.D三个图像中,与y轴平行的直线均与函数图像有只有一个交点,所以都是函数图像,即y是x的函数;只有B中有两个交点,故B不是函数.
【分析】根据函数的定义,给定一个自变量的值,函数值有唯一确定的值和它相对应可知B不是。
2.【答案】
D
解:根据题意得:x≥0且3-x≠0,
∴
的取值范围是x≥0且x≠0.
故答案为:D.
3.【答案】
B
解:∵
中,k=-2<0,b=3>0,
∴一次函数过第一、二、四象限,不经过第三象限,
故答案为:B.
4.【答案】
B
解:根据题意,将直线y=2x﹣1向左平移1个单位后得到的直线解析式为:
y=2(x+1)﹣1,即y=2x+1,
故答案为:B.
5.【答案】
D
解:分两种情况:(1)当k>0时,正比例函数y=kx的图象过原点、且过第一、三象限,一次函数y=k(1﹣x)=﹣kx+k的图象经过第一、二、四象限,选项D符合;
(2.)当k<0时,正比例函数y=kx的图象过原点、第二、四象限,一次函数y=k(1﹣x)=﹣kx+k的图象经过第一、三、四象限,无选项符合.
故选D.
6.【答案】
B
解:∵
随
的增大而增大,
∴
?,
?,故答案为:B.
7.【答案】
B
解:因为正比例函数y=kx(k≠0)的图象经过第二、四象限,
所以k<0,
所以一次函数y=x+k的图象经过一、三、四象限,
故选B
【分析】根据正比例函数经过第二、四象限,得出k的取值范围,进而解答即可.
8.【答案】
B
解:∵点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=4x+2上,
∴y1=﹣2×4+2=﹣6,y2=﹣1×4+2=﹣2,y3=1×4+2=6.
∵﹣6<﹣2<6,
∴y1<y2<y3
.
故选B.
9.【答案】
A
解:∵在矩形ABCD中,AB=2,AD=3,
∴CD=AB=2,BC=AD=3,
∵点E是BC边上靠近点B的三等分点,
∴CE=
×3=2,
①点P在AD上时,△APE的面积y=
x?2=x(0≤x≤3),
②点P在CD上时,S△APE=S梯形AECD﹣S△ADP﹣S△CEP
,
=
(2+3)×2﹣
×3×(x﹣3)﹣
×2×(3+2﹣x),
=5﹣
x+
﹣5+x,
=﹣
x+
,
∴y=﹣
x+
(3<x≤5),
③点P在CE上时,S△APE=
×(3+2+2﹣x)×2=﹣x+7,
∴y=﹣x+7(5<x≤7),
故选:A.
10.【答案】
B
解:依题可得:
A(4,0),B(0,4),
设光线射在OB的点N处,作点P关于OB的对称点P1
,
作点P关于AB的对称点P2
,
如图:
由反射规律可知点P1、Q、N、P2四点共线,
∵P(2,0),
∴P1(-2,0),
设P2(x,y),
∴
,
解得:
,
设直线P1P2解析式为y=kx+b,
∴
,
解得:
,
∴直线P1P2解析式为y=x+
,
∴
,
解得:
,
∴Q(
,
).
故答案为:B.
二、填空题
11.【答案】
-3
解:∵函数y=(a-3)x|a|-2+2a+1是一次函数,
∴a=±3,
又∵a≠3,
∴a=-3.
故答案为:-3.
12.【答案】
y=2x+2
解:设该直线方程是:y=kx+b(k>0).
根据图象知,该直线经过点(﹣1,0)、(0,2),
则
,解得,
,
∴此函数的解析式为y=2x+2.
故答案是:y=2x+2.
13.【答案】
y=5x+6
解:由题意得
y=(x+2)
×5-4,即y=5x+6.
【分析】由运算程序可知y=(x+2)
×5-4,整理即可求解。
14.【答案】
m=-1;减小
解:∵此函数是一次函数,
∴|m|=1且m-1≠0
解之:m=±1.且m≠1
∴m=-1
故答案为:m=-1
15.【答案】
200
解:设队伍前进时的函数关系式为y=kx,
把点(24,1200)代入得:1200=24k,
解得:k=50,
∴解析式为y=50x,
队伍走到展览馆所用的时间为:2000÷50=40(分钟),
则小亮返回之后队伍走到展览馆所用的时间为:40-24=16(分钟),
根据图象可知,小亮返回之后到到达展览馆走的路程为:1200+2000=3200米,
∴小亮跑步的速度为:3200÷16=200(米/分钟)
故答案为:200.
三、解答题
16.【答案】
(1)y=-x+40
(2)解:200元
解:(1)设y与x的函数解析式为y=kx+b,
∵,
∴
解之:
∴y=-x+40
(2)当x=30时,每日的销售利润=(-30+40)(30-10)=200
【分析】(1)利用待定系数法,求出y与x的函数解析式即可。
(2)每日的销售利润=(售价-进价)×销售量y,计算即可求出答案。
17.【答案】
(1)解:利用函数性质,4-2m<0,所以m<-2
(2)解:由题意得m-4<0,解得m<4
(3)解:由题意得
,
解得-2<m<4.
所以当m>4时图象经过第一、三、四象限.
(4)解:由题意得
,
解得m>4.
所以当-2<m<4时图象经过第一、二、三象限。
解:(1)利用一次函数性质,可知k0,即4-2m0,求得m取值范围即可。
(2)令x=0,由题意得y=m-40,求得m取值范围。
(3)图象经过第一、三、四象限,根据图像性质可知,k0,b0,即4+2m0、m?40,列不等式组求解。
(4)当图象过第一、二、三象限时,k0,b0,即4+2m0、m?40,列不等式组求解m的取值范围即可。
四、综合题
18.【答案】
(1)解:设
,
,由题意得:将
,
分别代入即可:
,
,
,
故所求的解析式为
;
(2)解:当通讯时间相同时
,得
,解得
.
答:通话300分钟时两种收费方式费用相等
19.【答案】解:(1)2400÷96=25(min)
∴点E、F的坐标为(0,2400)(25,0)
设EF的函数关系式为S2="kt+b,"
则有
,解得,
∴S2=-96t+2400.
(2)B、D点的坐标为(12,2400)、(22,0).得BD段的函数关系式为y=﹣240x+5280,
与S2=-96t+2400的交点坐标为(20,480)
所以小明从家出发,经过20分钟在返回途中追上爸爸,这时他们距离家480m.
.
20.【答案】
(1)解:∵一次函数y=k1x+b过点A(-3,0);
C(3,4)
??????
∴
????
解得:
?
∴一次函数关系式为y=
x+2
∵正比例函数y=kx的图象过点为C(3,4)
∴4=-3k2
∴k2=
???
正比例函数:y=
x
(2)解:如图所示,作D1M⊥X轴于M点,作D2N⊥Y轴于N,在等腰△AD1B中,
?
A
D1=AB
;?
∠D1AB=90°??
∠D1DA=∠AOB=90°
∴∠D1AM+∠BAO=90°???
又∵∠ABO+∠BAO=90°
∴∠D1AM
=∠BAO
在△D1DA与△
OAB中
????
∠D1AM
=∠BAO(已证)
?????
∠D1MA=∠AOB(已证)
?????
A
D1=AB
(已证)
∴△D1MA≌△OAB(AAS)
∴D1
M=OA=3;AM=BO=2??
∴OM=5
∵D1在第二象限,∴D1(-5,3)
同理证:△D2NB≌△BOA(AAS)?
∴D2(-2,5)
(3)解:存在;作C关于X轴对称点C1
,
连接BC1
,
交X轴于E,此时△BCE周长最小。∵
∴
∴BC1的解析式为:y=-2x+2
令y=0,得0=-2x+2,
x=1
∴E点的坐标为(1,0)
(4)解:P
(5,0)
????
P
(-5,0)
????
P?
(6,
0)
????
P?
(
,0)
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册第四单元
一次函数
单元练习
一、单选题
1.下列各种图象中,y不是x的函数的是(???
)
A.?????????B.?????????C.?????????D.?
2.函数
中自变量
的取值范围是(?
)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
3.直线
不经过的象限是
(???
)
A.?第四象限???????????????????????????B.?第三象限???????????????????????????C.?第二象限???????????????????????????D.?第一象限
4.把直线y=2x﹣1向左平移1个单位,平移后直线的关系式为(?
)
A.?y=2x﹣2???????????????????????????????B.?y=2x+1???????????????????????????????C.?y=2x???????????????????????????????D.?y=2x+2
5.正比例函数y=kx(k≠0)和一次函数y=k(1﹣x)在同一个直角坐标系内的图象大致是下图中的(??
)
A.???????????B.???????????C.???????????D.?
6.已知一次函数
.
若
随
的增大而增大,则
的取值范围是(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
7.正比例函数y=kx(k≠0)的图象经过第二、四象限,则一次函数y=x+k的图象大致是(??
)
A.??????????B.??????????C.??????????D.?
8.已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=4x+2上,则y1
,
y2
,
y3的值的大小关系是(??
)
A.?y3<y1<y2???????????????????????B.?y1<y2<y3???????????????????????C.?y3>y1>y2???????????????????????D.?y1>y2>y3
9.如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是(??
)
A.???????????B.???????????C.???????????D.?
10.如图,直线y=-x+4分别与x轴,y轴交于A,B两点.从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是(
??)
A.?(2,2)?????????????????????????????B.?(2.5,1.5)?????????????????????????????C.?(3,1)??????????????????????????????D.?(1.5,2.5)
二、填空题
11.若函数y=(a-3)x|a|-2+2a+1是一次函数,则a=________.
12.如图,该直线是某个一次函数的图象,则此函数的解析式为________.
13.按如图所示的运算程序,输入一个有理数x,便可输出一个相应的有理数y,写出y与x之间的关系式:________.
14.若函数
是一次函数,则m=________,且
随
的增大而________
15.某班带队到展览馆参观,并要求作好记录,小亮随队伍步行一段时间后,发现未带笔记本,随即跑步返回拿到笔记本后又以相同的速度追赶队伍,恰好与队伍在同一时间到达展览馆.行程与时间的关系如图所示,其中实线表示队伍的图象,虚线表示小亮的图象,则小亮跑步的速度为________米/分钟.
三、解答题
16.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
若日销售量y是销售价x的一次函数.
x
(元)
15
20
25
…
y
(件)
25
20
15
…
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
17.已知一次函数
,求:
(1)m为何值时,y随
的增大而减少??
(2)m为何值时,函数图象与y轴的交点在
轴下方?
(3)m为何值时,图象经过第一、三、四象限??
(4)图象能否过第一、二、三象限?
四、综合题
18.某通讯公司推出①、②两种收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
(1)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(2)何时两种收费方式费用相等?
19.小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min的速度从邮局沿同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t
min时,小明与家之间的距离为
S1
m,小明爸爸与家之间的距离为S2
m,图中折线OABD,线段EF分别是表示S1、S2与t之间函数关系的图像.
(1)求S2与t之间的函数关系式:
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
20.如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)求正比例函数与一次函数的关系式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
(4)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
答案解析部分
一、单选题
1.【答案】
B
解:过x轴上一点作x轴的垂线,若与函数图像有且仅有一个交点,则该图像表示函数的图像;若与函数图像有不止一个交点,则该图像不是函数图像.在A.C.D三个图像中,与y轴平行的直线均与函数图像有只有一个交点,所以都是函数图像,即y是x的函数;只有B中有两个交点,故B不是函数.
【分析】根据函数的定义,给定一个自变量的值,函数值有唯一确定的值和它相对应可知B不是。
2.【答案】
D
解:根据题意得:x≥0且3-x≠0,
∴
的取值范围是x≥0且x≠0.
故答案为:D.
3.【答案】
B
解:∵
中,k=-2<0,b=3>0,
∴一次函数过第一、二、四象限,不经过第三象限,
故答案为:B.
4.【答案】
B
解:根据题意,将直线y=2x﹣1向左平移1个单位后得到的直线解析式为:
y=2(x+1)﹣1,即y=2x+1,
故答案为:B.
5.【答案】
D
解:分两种情况:(1)当k>0时,正比例函数y=kx的图象过原点、且过第一、三象限,一次函数y=k(1﹣x)=﹣kx+k的图象经过第一、二、四象限,选项D符合;
(2.)当k<0时,正比例函数y=kx的图象过原点、第二、四象限,一次函数y=k(1﹣x)=﹣kx+k的图象经过第一、三、四象限,无选项符合.
故选D.
6.【答案】
B
解:∵
随
的增大而增大,
∴
?,
?,故答案为:B.
7.【答案】
B
解:因为正比例函数y=kx(k≠0)的图象经过第二、四象限,
所以k<0,
所以一次函数y=x+k的图象经过一、三、四象限,
故选B
【分析】根据正比例函数经过第二、四象限,得出k的取值范围,进而解答即可.
8.【答案】
B
解:∵点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=4x+2上,
∴y1=﹣2×4+2=﹣6,y2=﹣1×4+2=﹣2,y3=1×4+2=6.
∵﹣6<﹣2<6,
∴y1<y2<y3
.
故选B.
9.【答案】
A
解:∵在矩形ABCD中,AB=2,AD=3,
∴CD=AB=2,BC=AD=3,
∵点E是BC边上靠近点B的三等分点,
∴CE=
×3=2,
①点P在AD上时,△APE的面积y=
x?2=x(0≤x≤3),
②点P在CD上时,S△APE=S梯形AECD﹣S△ADP﹣S△CEP
,
=
(2+3)×2﹣
×3×(x﹣3)﹣
×2×(3+2﹣x),
=5﹣
x+
﹣5+x,
=﹣
x+
,
∴y=﹣
x+
(3<x≤5),
③点P在CE上时,S△APE=
×(3+2+2﹣x)×2=﹣x+7,
∴y=﹣x+7(5<x≤7),
故选:A.
10.【答案】
B
解:依题可得:
A(4,0),B(0,4),
设光线射在OB的点N处,作点P关于OB的对称点P1
,
作点P关于AB的对称点P2
,
如图:
由反射规律可知点P1、Q、N、P2四点共线,
∵P(2,0),
∴P1(-2,0),
设P2(x,y),
∴
,
解得:
,
设直线P1P2解析式为y=kx+b,
∴
,
解得:
,
∴直线P1P2解析式为y=x+
,
∴
,
解得:
,
∴Q(
,
).
故答案为:B.
二、填空题
11.【答案】
-3
解:∵函数y=(a-3)x|a|-2+2a+1是一次函数,
∴a=±3,
又∵a≠3,
∴a=-3.
故答案为:-3.
12.【答案】
y=2x+2
解:设该直线方程是:y=kx+b(k>0).
根据图象知,该直线经过点(﹣1,0)、(0,2),
则
,解得,
,
∴此函数的解析式为y=2x+2.
故答案是:y=2x+2.
13.【答案】
y=5x+6
解:由题意得
y=(x+2)
×5-4,即y=5x+6.
【分析】由运算程序可知y=(x+2)
×5-4,整理即可求解。
14.【答案】
m=-1;减小
解:∵此函数是一次函数,
∴|m|=1且m-1≠0
解之:m=±1.且m≠1
∴m=-1
故答案为:m=-1
15.【答案】
200
解:设队伍前进时的函数关系式为y=kx,
把点(24,1200)代入得:1200=24k,
解得:k=50,
∴解析式为y=50x,
队伍走到展览馆所用的时间为:2000÷50=40(分钟),
则小亮返回之后队伍走到展览馆所用的时间为:40-24=16(分钟),
根据图象可知,小亮返回之后到到达展览馆走的路程为:1200+2000=3200米,
∴小亮跑步的速度为:3200÷16=200(米/分钟)
故答案为:200.
三、解答题
16.【答案】
(1)y=-x+40
(2)解:200元
解:(1)设y与x的函数解析式为y=kx+b,
∵,
∴
解之:
∴y=-x+40
(2)当x=30时,每日的销售利润=(-30+40)(30-10)=200
【分析】(1)利用待定系数法,求出y与x的函数解析式即可。
(2)每日的销售利润=(售价-进价)×销售量y,计算即可求出答案。
17.【答案】
(1)解:利用函数性质,4-2m<0,所以m<-2
(2)解:由题意得m-4<0,解得m<4
(3)解:由题意得
,
解得-2<m<4.
所以当m>4时图象经过第一、三、四象限.
(4)解:由题意得
,
解得m>4.
所以当-2<m<4时图象经过第一、二、三象限。
解:(1)利用一次函数性质,可知k0,即4-2m0,求得m取值范围即可。
(2)令x=0,由题意得y=m-40,求得m取值范围。
(3)图象经过第一、三、四象限,根据图像性质可知,k0,b0,即4+2m0、m?40,列不等式组求解。
(4)当图象过第一、二、三象限时,k0,b0,即4+2m0、m?40,列不等式组求解m的取值范围即可。
四、综合题
18.【答案】
(1)解:设
,
,由题意得:将
,
分别代入即可:
,
,
,
故所求的解析式为
;
(2)解:当通讯时间相同时
,得
,解得
.
答:通话300分钟时两种收费方式费用相等
19.【答案】解:(1)2400÷96=25(min)
∴点E、F的坐标为(0,2400)(25,0)
设EF的函数关系式为S2="kt+b,"
则有
,解得,
∴S2=-96t+2400.
(2)B、D点的坐标为(12,2400)、(22,0).得BD段的函数关系式为y=﹣240x+5280,
与S2=-96t+2400的交点坐标为(20,480)
所以小明从家出发,经过20分钟在返回途中追上爸爸,这时他们距离家480m.
.
20.【答案】
(1)解:∵一次函数y=k1x+b过点A(-3,0);
C(3,4)
??????
∴
????
解得:
?
∴一次函数关系式为y=
x+2
∵正比例函数y=kx的图象过点为C(3,4)
∴4=-3k2
∴k2=
???
正比例函数:y=
x
(2)解:如图所示,作D1M⊥X轴于M点,作D2N⊥Y轴于N,在等腰△AD1B中,
?
A
D1=AB
;?
∠D1AB=90°??
∠D1DA=∠AOB=90°
∴∠D1AM+∠BAO=90°???
又∵∠ABO+∠BAO=90°
∴∠D1AM
=∠BAO
在△D1DA与△
OAB中
????
∠D1AM
=∠BAO(已证)
?????
∠D1MA=∠AOB(已证)
?????
A
D1=AB
(已证)
∴△D1MA≌△OAB(AAS)
∴D1
M=OA=3;AM=BO=2??
∴OM=5
∵D1在第二象限,∴D1(-5,3)
同理证:△D2NB≌△BOA(AAS)?
∴D2(-2,5)
(3)解:存在;作C关于X轴对称点C1
,
连接BC1
,
交X轴于E,此时△BCE周长最小。∵
∴
∴BC1的解析式为:y=-2x+2
令y=0,得0=-2x+2,
x=1
∴E点的坐标为(1,0)
(4)解:P
(5,0)
????
P
(-5,0)
????
P?
(6,
0)
????
P?
(
,0)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
